
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитический расчет формы и натяжения гибких нитей.
Дифференциальные уравнения, описывающие форму гибкой нити и усилий в ней, имеют вид
где Т — натяжение нити в рассматриваемой точке; S — длина нити; q — вес в воде нити единичной длины; a — угол, образованный касательной к нити в рассматриваемой точке и горизонталью; R t, Rn — касательная и нормальная составляющие силы сопротивления нити единичной длины. Если нагрузка в нижней точке нити D равна нулю (T0 = 0), то нить примет форму прямой линии, находящейся под углом a к вектору v. Значение угла a в этом случае называется предельным и обозначается aПред. Гибкая нить сохраняет прямолинейную форму, если составляющие усилия Т0, приложенного к нижнему концу, находятся в соотношении ToyJT0x=tgaПpeд (2.2) Таким образом, гибкая нить, закрепленная в верхней точке и находящаяся под действием сил тяжести и гидродинамического давления воды, может принять форму прямой линии при условии aО = a = aПpeд;(2.3) кривой, обращенной выпуклостью вниз, при условии aо < a < aПpeд; (2.4) кривой, обращенной выпуклостью вверх, при условии aо > a > aПpeд. (2.5) Угол атаки нити прямолинейной формы вычисляется по формуле
где с — коэффициент сопротивления ваера, расположенного перпендикулярно вектору скорости (с ≈1,1); d — диаметр троса. Нить, обращенная выпуклостью вниз (см. рис. 4), схематизирует форму ваера. Если пренебречь малой величиной тангенциальной составляющей полного давления воды (Rx = 0), то координаты любой точки нити (ваера) вычисляются по формулам:
По формуле (2.6,6) вычисляется горизонт хода YА нижнего конца ваера. По формуле (2.7) — расстояние по горизонтали ХА между судном и траловой доской. Угол атаки a любого элемента нити (ваера), в том числе в точке А крепления ваера на судне, находится по формуле
Длина гибкой нити (ваера) находится из выражения
Натяжение в нижней точке D гибкой нити (ваера) находится как T0 = T2оx, + T2oу. (2.20) При расчете характеристик ваера составляющие усилия Т0 определяются по формулам: Тох=0,5(Rс.ч+Rос) +Rхд; (2.21) Т0у= (G Д ,+Gосн)-NГP (2.22)
Усилие в любой точке нити (ваера) без учета действия тангенциальной составляющей давления воды определяется выражением Рис.2.2 T = T0+qy. (2.23) При длине ваера более 1000 м необходимо учитывать влияние сил Rx и для расчета усилия в верхней точке ваера вместо (2.23) использовать формулу T = T0+qy + RxS. (2.24) Сила сопротивления ваера при движении в воде находится из выражения Rb=Tcosa— TOcosaO. (2.25) Ваер может состоять из нескольких частей, отличающихся весом и диаметром троса. Расчетная схема для составного ваера показана на рис. 2.2. Характеристики ваера в этом случае определяются поэтапно. На первом этапе рассчитываются характеристики участка ваера 00 1 для чего в качестве начальных условий используются значения силы Т0 и угла aO. По формулам (2.7) и (2.6,б) находятся координаты точки 01 — x1 и y1 по формуле (3.16) рассчитывается значение угла a1 по формуле (2.17)—длина первого участка ваера S1 по формулам (2.23) или (2.24)—усилие Т1 в точке ваера O1. На втором этапе рассчитываются характеристики участка ваера O1А. При этом начальными условиями являются: Т0=Т1 и a0= a. По указанным формулам для второго участка находятся значения х2, у2, a2, S2, Т2. Характеристики составного ваера определяются как:
xA=x1+ x2; (2.26) yа=y1 + y2; (2.27) S = S1 + S2. (2.28) Сопротивление составного ваера RB = T2cosa2— Tосоs а о. (2.29) Гибкая нить, обращенная выпуклостью вниз, схематизирует также форму сети, нижняя подбора которой закреплена на грунте. С помощью гибкой нити, обращенной выпуклостью вверх, схематизируется форма деталей орудий лова, как, например, кабель сетного зонда или сеть, закрепленная у поверхности воды за верхнюю подбору.
Замена цепной линии параболой. Для упрощения расчетов цепную линию часто заменяют параболой. Гибкая нить принимает форму параболы, если внешние силы равномерно распределены по ее хорде (проекции АВ на рис. 2.3). Уравнение параболы имеет вид
или
где Длина нити, имеющей форму параболы, от вершины до точки закрепления (ОА на рис. 20) приближенно может быть определена из выражения Рис. 2.3
Половина хорды нити вычисляется в этом случае по формуле
Горизонтальная составляющая натяжения Т0 в нити, имеющей форму параболы, находится как TO = qL2/2f. (2.47) Натяжение Т в гибкой нити, как и ранее, определяется на основании зависимости (2.23). Если точки закрепления нити расположены на разных уровнях, то значение горизонтальной составляющей натяжения Т0 зависит от взаимного расположения вершины нити и точек ее подвеса. Возможны три варианта такого взаимного расположения. Если вершина С находится между точками подвеса (рис. 2.4), то значение Т0 будет минимальным и находится по формуле
Если воображаемая вершина нити находится вне точек подвеса, то значение Т0 будет максимальным и определяется по формуле
Третий вариант имеет место, когда одна из точек подвеса совмещена с вершиной кривой. Тогда Т0 принимает среднее значение и подсчитывается из выражения
Учет растяжения гибкой нити. Реальные нитки, веревки и канаты существенно растягиваются под воздействием внешней нагрузки, в связи с чем возникающие в них усилия будут несколько меньше расчетных, а прогиб — больше расчетного. С учетом растяжения гибкой нити (форма которой соответствует параболе) горизонтальная составляющая натяжения Т0 и стрелка прогиба f находятся из выражений:
где s—относительное удлинение нити под нагрузкой. Q = 2qL: (2.59) Зависимость e=f/(T) определяется свойствами материала, из которого изготовлена нить. Стальные канаты подчиняются закону Гука, поэтому для них e=Т/EF; (2.60) где Е — модуль упругости стального каната, Н/м2; F — площадь поперечного сечения каната, м2. С учетом (3.60) для стальных канатов вместо выражений (2.57) и (2.58) следует использовать:
Для растительных канатов (пеньковых) можно принять
В связи с этим выражения для расчета горизонтальной составляющей натяжения в канате и стрелки прогиба принимают вид:
Гибкая нить под действием сосредоточенных сил. Если к гибкой нерастяжимой нити приложена одна сосредоточенная сила R, а точка ее приложения может перемещаться (внешняя сила приложена к кольцу, через которое проходит канат), то без учета сил трения (между кольцом и канатом) натяжения Т в ветвях нити будут одинаковыми и вычисляются по формуле
где b — угол между ветвями каната. С учетом сил трения натяжения в ветвях нити отличаются на величину силы трения. Если нить растягивается под действием сосредоточенной силы, то натяжения в ветвях снижаются по сравнению с результатом расчета по формуле (2.66). Для определения силы натяжения в этом случае необходимо знать зависимость s = f(T) для материала, из которого изготовлена рассматриваемая нить. Гибкая нерастяжимая нить, находящаяся под действием нескольких сосредоточенных сил R1, R2..., различных по величине и направлению, принимаем форму многоугольника. Если точки приложения сил имеют возможность перемещаться, то без учета сил трения натяжения во всех ветвях нити будут одинаковыми и вычисляются по формуле где b1 b2,. — углы между соответствующими ветвями каната
Вопросы для самоконтроля 1. Как определяются усилия в нитях, нагруженных сосредоточенными силами. 2. В каких случаях нить нагруженная распределённой силой принимает форму тяжелой нити? Как определить её форму и натяжение? 3. В каких случаях нить нагруженная распределённой силой принимает форму параболы? Как определить её форму и натяжение? 4. Опишите метод определения натяжения в ваере. 2.2 Форма и натяжение гибкой нити под действием одной сосредоточенной внешней силы. Если к гибкой нерастяжимой и невесомой нити, закрепленной в двух точках, приложена внешняя сила R, величина и направление которой известны, а точка приложения неподвижна (закреплена) то натяжение в ветвях нити находится графическим построением.
Пример 1. Канат 01А02 длиной 10,8 м закреплен в двух точках, находящихся на одном уровне на расстоянии 10 м (рис. 2.5). В центре каната висит кольцо А, к которому приложена сила R, равная 200 Н. Коэффициент трения кольца по канату f=0,5. Определить, при каком угле b между направлением силы R и вертикалью кольцо начнет скользить по канату. Найти величину сил натяжения в ветвях каната.
Решение. Для изображения каната на чертеже (рис. 2.5) выберем линейный масштаб, равный 0,01. В этом масштабе отложим заданное расстояние между точками закрепления нити O1и О 2. Из полученных точек раствором циркуля, равным в масштабе 5,4 м, сделаем засечки, определив тем самым положение кольца А. Точку А соединим с точками О1и О2. Выберем масштаб сил, приняв силу R равной отрезку CD. Рис. 2.5 Натяжение в ветвях нити отличается на величину силы трения, т. е.
На линии действия силы Т2 (АО2) от точки А отложим величину силы трения, равную 100 Н. Из точки В раствором циркуля, равным R, сделаем засечку на вертикали. Из полученной точки Е проводим луч, параллельный отрезку АО1 до пересечения с продолжением отрезка О2А. Треугольник AFE по построению равнобедренный, в котором AF = FE = T1. Тогда очевидно, что в полученном силовом треугольнике FBE имеем: FB = T2 и BE = R. Угол b непосредственно снимается с чертежа и равен 30°. Таким образом, при b ≤30° кольцо останется в покое, при b>30° оно начнет перемещаться по канату влево. Для определения натяжений в ветвях каната измерим отрезки EF и FB. С учетом принятого силового масштаба получим: T1 = 180 Н и T2=280Н. Форма и натяжение гибкой нити под действием нескольких сосредоточенных или распределенных сил. Когда кгибкой нерастяжимой и невесомой нити приложено несколько сосредоточенных сил, точки приложения которых закреплены, то ее форма и натяжение в ветвях находятся путем построения силового и веревочного многоугольника. К такой категории задач относится, например, определение формы и натяжения секции, хребтины яруса, находящейся под воздействием нескольких попавших на крючок рыб. Пример 2. Судно стоит на якоре, отдав 100 м цепного каната, сила веса в воде 1 м которого равна 100 Н (рис. 2.6). Ветровое сопротивление судна составляет 8000 Н. Глубина места стоянки судна на якоре равна 60 м. Определить форму каната, натяжения в верхнем и нижнем его концах и их горизонтальные и вертикальные составляющие. Решение. Назначим силовой масштаб, в соответствии с которым отрезок АВ равен 1000 Н (рис. 2.7). Направление силы ветрового сопротивления судна R горизонтально, поэтому на горизонтальной линии отложим отрезок Рс, равный в масштабе 800 Н. Вес цепного каната в воде составит G = 100·100=10 000 H. Направление силы G вертикально, поэтому из точки с восстановим перпендикуляр и на нем отложим отрезок сО, равный в масштабе 10 000 Н. Силы натяжения на концах цепного каната нам неизвестны, поэтому отсутствуют основания для однозначного выбора полюса. Вместе с тем задана длина цепного каната, что позволяет получить единственное решение путем осуществления последовательных приближений.
В первом приближении примем, что направление усилия в нижней точке каната горизонтально, и назначим полюсом точку Р. Соединив ее с точкой О, получим силовой треугольник РОс. Примем линейный масштаб равным 0,001. Цепной канат разделим на 10 равных частей по 10 м каждая. Вес участка каната в воде составит 1000 Н. В соответствии с этим разделим отрезок Ос также на 10 частей. Получим отрезки On, nm, ml,...,dc, представляющие собой силы веса участков каната в воде. Соединим точки п, т,..., d с полюсом Р прямыми линиями. Полученные отрезки определяют по величине и направлению усилия в соответствующих участках цепного каната.
Из точки O2 (рис. 2.7) проведем луч, параллельный отрезку РО, и отложим на нем половину участка каната, так как первая ветвь веревочного многоугольника ограничивается линией действия результирующей сил веса первого участка каната, проходящей через его центр. Из полученной точки N проводим луч, паралтельный отрезку Рп, на котором откладываем в масштабе полную длину участка каната 10 м, равную расстоянию между 1-й и 2-й результирующей сил веса на участках. Из полученной точки М проводим луч, параллельный отрезку Рт, на котором также откладываем 10-метровую длину участка каната. Таким образом, продолжаем построение, последовательно получая точки L, К, Н,..., С. Из точки С проводим луч, параллельный отрезку Рс, на котором откладываем половину последнего участка, равную 5 м. Таким образом, ломаная О2NML... O′, определяющая в первом приближении форму каната, по построению равна его длине, т. е. 100 м. Однако ордината точки О', как видно из рис. 2.7, меньше заданной глубины 60 м. Это свидетельствует о необходимости изменить положение полюса, причем следует обеспечить выполнение двух условий: горизонтальная составляющая R натяжения в нижней точке каната должна остаться прежней и равной 8000 Н, для достижения глубины 60 м ветви веревочного многоугольника должны быть расположены более круто. Учитывая сказанное, переносим полюс по вертикали вниз в точку Р1. Строим силовой треугольник во втором приближении, для чего точку P1 соединяем с точками О, п, т,..., с. Далее во втором приближении осуществляем построение веревочного многоугольника, выполняя те же операции, что и в предыдущем случае. Получаем ломаную О2N1M1L1... О′ 1, равную в масштабе 100 м. Как и ранее, ордината точки О1 не равна 60, что говорит о необходимости продолжить приближения. В третьем приближении переносим полюс по вертикали вниз в точку Р2 и соединяем ее с точками О, п, т,..., с. Осуществляем построение веревочного многоугольника ON2M2... О′2. Как видим, ордината точки О′2 равна 60 м, что и требовалось по условию задачи. Таким образом, форма цепного каната соответствует кривой, вписанной в ломаную O2N2M2L2... О′2. Натяжение в верхней точке цепного каната определяется отрезком Р2О. Измерив его и учтя масштаб сил, получим Т=14,3 кН. Горизонтальная составляющая этой силы равна R, т. е. 8 кН. Вертикальная составляющая ТY снимается с чертежа на рис. 2.7 и равна 12 кН. Сила натяжения нижнего конца каната определяется отрезком Р2с. Получаем T0 = 8,2 кН. Горизонтальная составляющая Т0х также равна R, т. е. 8 кН. Вертикальная составляющая Т0Y, стремящаяся оторвать якорь от грунта, определяется отрезком Р2Р. Получаем Т0Y = 2кН. Пример 3. Ставная сеть установлена на грунте в водоеме глубиной 5 м. Нижняя подбора закреплена на дне балластом. Верхняя удерживается на поверхности силой плавучести оснастки верхней подборы и наклонной оттяжкой (рис. 2.8). Пренебрегая влиянием натяжения в наклонной оттяжке, определить потребную высоту сети для обеспечения ей симметричной формы. Гидродинамическое сопротивление сети на 1 м ее длины R в результате воздействия течения составляет 100 Н, сила плавучести оснастки верхней подборы (на 1 м длины) Q = 40 H.
Рис.2.8 Рис.2.9 Строим силовой треугольник (рис. 2.9). Для этого из точки а последовательно откладываем по одной прямой (так как мы приняли, что на полоску сети действует система параллельных сил) результирующие сил гидродинамического давления воды на участки хорды r1, r2 r3, r4, r5. Отрезок af определяет полное давление воды R на сеть. Для определения полюса воспользуемся следующими соображениями. Так как форма полоски должна быть симметрична, то следует полагать, что в точках закрепления полоски А и В (см. рис. 2.8) приложены силы R/2. Из условия равновесия узла А следует, что топящая сила Т0 равна силе плавучести Q. Поэтому из центра отрезка af (точка К на рис. 2.9, а) восстанавливаем перпендикуляр, на котором откладываем величину Q. Получаем положение полюса Р. Соединяем точку Р с точками а, Ъ, с, d, e, f. Отрезки Ра и Pf силового треугольника определяют величину и направление реакций в точках закрепления полоски, отрезки Pb, Pc, Pd и Ре — натяжения в соответствующих участках сети. Для построения веревочного многоугольника выберем линейный масштаб равным 0,01. Пятиметровый отрезок AG разделим на пять равных частей и через центр каждой проведем линии действия сил ri, i=l, 2, 3, 4, 5 (рис. 2.9, б). Из точки А проведем луч, параллельный отрезку Ра, до пересечения с линией действия силы гь Из полученной точки В проведем луч, параллельный отрезку РЬ силового треугольника, до пересечения с линией действия силы г2 и т. д. до получения формы полоски сети в виде ломаной ABCDEFG. Измерив длину этой ломаной и учтя линейный масштаб, получим, что потребная высота сети должна быть равна 6 м. Если бы в условиях задачи была задана не глубина водоема, перекрываемая сетью, а ее высота, то для определения формы сети построение веревочного многоугольника необходимо осуществить следующим образом (рис. 2.9, в). Разделим заданную высоту на пять равных частей. Из точки А1 проведем луч, параллельный отрезку Ра силового треугольника, и на нем отложим половину длины участка сети. Из полученной точки В1 проведем луч, параллельный отрезку Рb, и на нем отложим длину участка и т. д. до получения формы полоски сети в виде ломаной A1B1C1D1E1F1G1. Тогда отрезок A1G1 определит (в масштабе) часть глубины водоема, которую перекроет сеть заданной высоты.
Рис. 2.10 Решение. Разобьем канат на шесть равных частей. Отметим центр каждой части точками С, D, E, F, G, К. Будем считать, что в этих точках приложены равнодействующие внешних сил, распределенных по длине участков. Заменим кривую АВ ломаной ACDEFGKB. Так как гидродинамическим сопротивлением каната по условию задачи можно пренебречь, то внешними силами являются силы трения. На каждый участок каната действует сила трения, равная 20-10-0,5= 100 Н. Примем, что отрезок LM на рис. 2.10 соответствует 100 Н. Из произвольного полюса Р проведем пучок лучей, каждый из которых параллелен соответственно отрезкам ACf CD, DE, EF, FG, GK и КВ. На первом луче в принятом силовом масштабе отложим силу 400 Н, приложенную к точке А. Из полученной точки с раствором циркуля, равным отрезку LM (величина силы трения, приложенная к каждому участку каната), делаем засечку на соседнем луче и получаем точку d. Из последней тем же раствором циркуля делаем засечку на следующем луче, получая точку е. Таким образом продолжаем построение, отмечая точки f, g, k и п и соединяя их прямыми линиями. Отрезок Рп характеризует величину и направление искомой силы Т2, приложенной к концу каната В. Измерив отрезок Рп и учтя масштаб, получим Т2 = 820 Н. Отрезки Pd, Pe, Pf, Pg, Pk характеризуют величину и направление соответствующих участков каната. Для определения направления результирующих сил трения, действующих на каждый участок каната, из точек С, D, E, Ff G, К проведем лучи, параллельные отрезкам соответственно cd, de, ef, fg, gk, kn. Эти лучи, отмеченные на рис. 2.10 цифрами 1, 2,..., 6, показывают направление системы внешних сил, под действием которых канат принял форму ломаной ACDEFGKB. Подобными построениями, например, может быть определена форма урезов донного невода в процессе их выборки (или буксировки невода). Вопросы для самоконтроля 1.Опишите порядок построения формы цепной линии. 2.Опишите порядок построения формы сети нагруженной силой сопротивления. 3.Опишите порядок построения формы уреза, буксируемого по грунту.
Литература: [1], стр. 69-75.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 1219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.21.86 (0.055 с.) |
 Гибкая нить под действием сил тяжести и гидродинамического сопротивления. Большинство орудий промышленного рыболовства представляет собой пространственные сетные конструкции, оснащенные системой канатов. Для расчета формы и нагрузок, возникающих в канатах, последние рассматриваются как гибкие нити, определенным образом закрепленные и находящиеся под действием внешних сил. При определении формы и нагрузок сетных элементов орудий используются расчетные схемы, в которых сети также заменяются гибкими нитями. Для этого из сети двумя вертикальными (или горизонтальными) сечениями вырезается элементарная полоска, свойства которой аналогичны свойствам гибкой нити. Для расчета деталей орудий лова в виде гибких нитей используется ряд типовых расчетных схем. Одна из них имеет вид, показанный на рис. 2.1.
Гибкая нить под действием сил тяжести и гидродинамического сопротивления. Большинство орудий промышленного рыболовства представляет собой пространственные сетные конструкции, оснащенные системой канатов. Для расчета формы и нагрузок, возникающих в канатах, последние рассматриваются как гибкие нити, определенным образом закрепленные и находящиеся под действием внешних сил. При определении формы и нагрузок сетных элементов орудий используются расчетные схемы, в которых сети также заменяются гибкими нитями. Для этого из сети двумя вертикальными (или горизонтальными) сечениями вырезается элементарная полоска, свойства которой аналогичны свойствам гибкой нити. Для расчета деталей орудий лова в виде гибких нитей используется ряд типовых расчетных схем. Одна из них имеет вид, показанный на рис. 2.1.
 (2.1)
(2.1)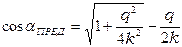 (2.6)
(2.6)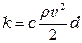 , (2.6,а)
, (2.6,а) (2.6,б)
(2.6,б) (2.7)
(2.7)
 (2.14)
(2.14)
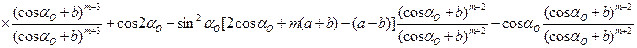 (2.15).
(2.15).

 где Rс у — сопротивление канатно-сетной части трала, Н; R0c — сопротивление оснастки подбор трала, Н; RXД — лобовое сопротивление траловой доски, Н; Gосh — половина веса оснастки трала в воде, Н; вя — вес траловой доски в воде, Н; NГР — реакция грунта при движении донной траловой доски по грунту [приближенно равно (0,4-0,7) Gд].
где Rс у — сопротивление канатно-сетной части трала, Н; R0c — сопротивление оснастки подбор трала, Н; RXД — лобовое сопротивление траловой доски, Н; Gосh — половина веса оснастки трала в воде, Н; вя — вес траловой доски в воде, Н; NГР — реакция грунта при движении донной траловой доски по грунту [приближенно равно (0,4-0,7) Gд]. y=x2/2р (3.43)
y=x2/2р (3.43) , x=p·tga. (3.44)
, x=p·tga. (3.44) – параметр гибкой нити.
– параметр гибкой нити.
 (2.46)
(2.46)

 (2.51)
(2.51)
 . (2.52)
Если для нити, точки подвеса которой находятся на разном уровне, заданными являются значения горизонтальной составляющее натяжения Т0, внешней нагрузки q, разницы абсцисс точек подвеса 2а и ординат 2b, то координаты точек подвеса, соответствующие этим значениям, могут быть вычислены по формулам:
. (2.52)
Если для нити, точки подвеса которой находятся на разном уровне, заданными являются значения горизонтальной составляющее натяжения Т0, внешней нагрузки q, разницы абсцисс точек подвеса 2а и ординат 2b, то координаты точек подвеса, соответствующие этим значениям, могут быть вычислены по формулам:
 Рис. 2.4
Рис. 2.4
 (2.53)
(2.53) (2.54)
(2.54) (2.55)
(2.55) (2.56)
(2.56)

 (2.63)
(2.63) ; (2.64)
; (2.64) . (2.65)
. (2.65) , (2.66)
, (2.66) , (2.67)
, (2.67)



 ГРАФОСТАТИЧЕСКИЙ РАСЧЕТ ФОРМЫ И НАТЯЖЕНИЯ ГИБКИХ НИТЕЙ, КАНАТОВ И СЕТЕЙ
ГРАФОСТАТИЧЕСКИЙ РАСЧЕТ ФОРМЫ И НАТЯЖЕНИЯ ГИБКИХ НИТЕЙ, КАНАТОВ И СЕТЕЙ

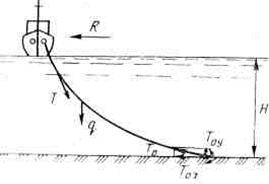
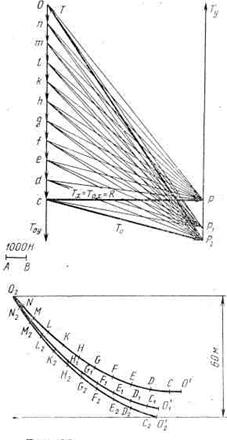 Рис.2.6 Рис.2.7
Рис.2.6 Рис.2.7
 Решение. Допустим, что отрезок АВ соответствует силе 10 Н (рис. 2.9, а). Будем полагать, что сила гидродинамического давления воды, воздействующая на полоску сети шириной 1 м, равномерно распределена по ее хорде и направлена ей перпендикулярно (как это показано на рис. 2.8). Разобьем хорду длиной 5 м на пять равных частей и к центру каждой из них приложим результирующую распределенной нагрузки, равную 20 Н.
Решение. Допустим, что отрезок АВ соответствует силе 10 Н (рис. 2.9, а). Будем полагать, что сила гидродинамического давления воды, воздействующая на полоску сети шириной 1 м, равномерно распределена по ее хорде и направлена ей перпендикулярно (как это показано на рис. 2.8). Разобьем хорду длиной 5 м на пять равных частей и к центру каждой из них приложим результирующую распределенной нагрузки, равную 20 Н.
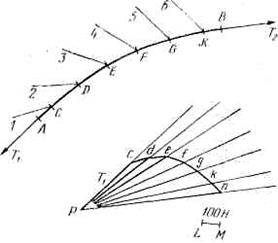 Пример 4. Канат длиной 60 м буксируют по дну за один конец. В некоторый момент времени он принял форму, показанную на рис. 2.10 в виде кривой АВ. Вес 1 м каната в воде 20 Н, коэффициент трения каната по грунту 0,5. К левому концу каната (точка А) приложена нагрузка, равная 400 Н. Пренебрегая гидродинамическим сопротивлением каната в воде,.определить буксировочное усилие, приложенное в точке В, и направление внешних сил, под действием которых он принял указанную форму.
Пример 4. Канат длиной 60 м буксируют по дну за один конец. В некоторый момент времени он принял форму, показанную на рис. 2.10 в виде кривой АВ. Вес 1 м каната в воде 20 Н, коэффициент трения каната по грунту 0,5. К левому концу каната (точка А) приложена нагрузка, равная 400 Н. Пренебрегая гидродинамическим сопротивлением каната в воде,.определить буксировочное усилие, приложенное в точке В, и направление внешних сил, под действием которых он принял указанную форму.
 Раздел 3. Механика сетей
Раздел 3. Механика сетей


