
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Элементы системы массового обслуживания (смо)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формулировка задачи и характеристики СМО
Часто на практике приходится сталкиваться с такими ситуациями: очередь покупателей в кассах магазинов; колонна автомобилей, движение которых остановлено светофором; ряд станков, вышедших из строя и ожидающих ремонта, и т.д. Все эти ситуации объединяет то обстоятельство, что системам необходимо пребывать в состоянии ожидания. Ожидание является следствием вероятностного характера возникновения потребностей в обслуживании и разброса показателей обслуживающих систем, которые называют системами массового обслуживания (СМО). Цель изучения СМО состоит в том, чтобы взять под контроль некоторые характеристики системы, установить зависимость между числом обслуживаемых единиц и качеством обслуживания. Качество обслуживания тем выше, чем больше число обслуживающих единиц. Но экономически невыгодно иметь лишние обслуживающие единицы. В промышленности СМО применяются при поступлении сырья, материалов, комплектующих изделий на склад и выдаче их со склада; обработке широкой номенклатуры деталей на одном и том же оборудовании; организации наладки и ремонта оборудования; определении оптимальной численности обслуживающих отделов и служб предприятий и т.д. Под системой массового обслуживания (СМО) будем понимать комплекс, состоящий из: а) случайного входящего потока требований (событий), нуждающихся в «обслуживании», б) дисциплины очереди, в) механизма, осуществляющего обслуживание. Входящий поток. Для описания входящего потока обычно задается вероятностный закон, управляющий последовательностью моментов поступления требований на обслуживание и количеством требований в каждом поступлении (то есть требования поступают либо единичные, либо групповые). Источник, генерирующий требования, считается неисчерпаемым. Требование, поступившее на обслуживание, может обслуживаться сразу, если есть свободные обслуживающие приборы, либо ждать в очереди, либо отказаться от ожидания, то есть покинуть обслуживающую систему. СМО можно разбить на две группы: - разомкнутые (источник входящих требований неиссякаемый - поток клиентов в парикмахерские, магазины, звонков на АТС и др.); - замкнутые (имеют ограниченный поток требований, например, выход прибора из строя и его восстановление). Дисциплина очереди. Это описательная характеристика. Требование, поступившее в систему обслуживается в порядке очереди – дисциплина очереди: «первым пришел – первым обслужен». Другая дисциплина очереди: «последним пришел – первым обслужен»- это обслуживание по приоритету. Наконец, обслуживание требований может быть случайным. Механизм обслуживания. Характеризуется продолжительностью и характером процедур обслуживания. Обслуживание может осуществляться по принципу: «на одно требование – один обслуживающий прибор». Если в системе несколько приборов, то параллельно могут обслуживаться несколько требований. Часто используют групповое обслуживание, то есть требование обслуживается одновременно несколькими приборами. В некоторых случаях требование обслуживается последовательно несколькими приборами – это многофазовое обслуживание. По окончании обслуживания требование покидает систему.
Рис. 4.1 Функционирование СМО представляется в виде связного графа ее состояний Сi, В стационарном (установившемся) режиме действует принцип равновесия: сумма «входов» в любое состояние равна сумме «выходов» из него. Это позволяет записать уравнения равновесия по каждому из состояний (принцип декомпозиции).
Рис. 4.2
Целью анализа системы массового обслуживания является рациональный выбор структуры обслуживания и процесса обслуживания. Для этого требуется разработать показатели эффективности систем массового обслуживания. Например, требуется знать: вероятность того, что занято или свободно k приборов; распределение вероятностей свободных или занятых приборов от обслуживания; вероятность того, что в очереди находится заданное число требований; вероятность того, что время ожидания в очереди превысит заданное. К показателям, характеризующих эффективность функционирования системы в среднем, относятся: средняя длина очереди; среднее время ожидания обслуживания; среднее число занятых приборов; среднее время простоя приборов; коэффициент загрузки системы и др. Часто вводятся экономические показатели. Разработкой математических моделей, получением числовых результатов и анализом показателей эффективности занимается теория массового обслуживания (ТМО).
4.2. Входящий поток требований
Случайным потоком событий называется появление однородных событий в случайные моменты времени. Рассмотрим временную ось (рис. 4.3). Поток событий представляет собой, вообще говоря, последовательность «случайных» точек
Рис. 4.3 Потоки событий различаются по законам распределения длин интервалов Наиболее изучены потоки, которые обладают следующими свойствами: а) стационарности – все его вероятностные характеристики не меняются со временем; б) отсутствия последействия – для любых непересекающихся временных интервалов на временной оси, число событий находящихся на одном интервале, не зависит от того, сколько их и как они оказались на другом интервале; в) ординарности – практическая невозможность на достаточно малом временном интервале появиться двум и более событиям. Для практического анализа важно знать, к какому виду можно отнести реальные потоки требований. В анализ входит нахождение функции распределения, управляющей входящим потоком и/или оценка ее параметров. Для этого необходимо: а) выбрать интервал времени, в течение которого поток требований практически стационарный; б) весь интервал разделить на достаточное число полуоткрытых непересекающихся промежутков, внутри каждого из которых подсчитывается число поступивших требований; в) построить гистограмму и найти эмпирическую функцию распределения; г) выдвинуть гипотезу о теоретическом аналоге эмпирического распределения; д) используя критерий е) в случае отрицательного результата либо проверяется репрезентативность выборки, или отвергается гипотеза.
1. Пуассоновский поток В подавляющем большинстве работ по ТМО рассматривается пуассоновский поток требований
где параметр l определяется как математическое ожидание числа требований, поступающих в СМО в единицу времени (или плотность потока, или интенсивность). Основание: а) количественная оценка качества функционирования СМО выражается в простых, относительно других видов потоков, аналитических зависимостях; б) при расчете показателей эффективности полученные результаты, как правило, отражают наиболее сложный случай (то есть показатели эффективности имеют более надежные значения). Если пуассоновский поток нестационарный, то есть,
2. Рекуррентный поток Так называется поток с ограниченным последействием - последовательность моментов Если все Часто поток с ограниченным последействием определяют как поток, у которого случайные интервалы Стационарный поток с ограниченным последействием называется потоком Пальма. Легко понять, что для него все случайные интервалы Примером потока Пальма является простейший поток (для потока независимого от времени – это геометрическое распределение, для непрерывного времени – это пуассоновский поток). Случайный стационарный поток, у которого все интервалы
3. Потоки Эрланга Поток Пальма, у которого интервалы времени между поступлениями требований являются случайной величиной с функцией распределения Эрланга
называется потоком Эрланга порядка k, В частности, поток Эрланга 1-го порядка является простейшим потоком, то есть,
Пусть требования, поступающие в систему, образуют простейший поток. Потоку Эрланга порядка k будет удовлетворять каждое k -ое из множества поступивших требований простейшего потока. То есть, поток Эрланга является «разряженным» простейшим потоком. Например, если у поступивших по закону простейшего потока в СМО требований учитывать каждое второе, то получаем поток Эрланга 2-го порядка, с функцией распределения
Следовательно, промежутки времени
Рис. 4.4 С помощью потоков Эрланга можно моделировать потоки Пальма с различным последействием. В самом деле, при Требование ограниченности последействия слабее, чем отсутствие последействие и, тем самым, охватывает более широкий круг практических задач.
4.3. Время обслуживания (выходящий поток требований)
Время обслуживания
В практических приложениях наиболее распространен экспоненциальный закон обслуживания требований
где интенсивность Время обслуживания требования Экспоненциальная функция распределения наиболее приближена к таким реальным случайным процессам, в которых большинство требований обслуживается быстро, что на практике не всегда выполняется. Пусть в СМО, состоящую из n разнотипных приборов, поступает случайный поток требований, каждое из которых обслуживают все приборы. Если время обслуживания определяется экспоненциальным законом распределения с интенсивностью
где В частности, если все обслуживающие устройства одинаковые, то их суммарная интенсивность (для экспоненциального закона)
то есть, при одинаковых обслуживающих устройствах среднее время обслуживания требования уменьшается в n раз,а дисперсия – в Это свойство справедливо только для экспоненциального распределения. Более общим, является эрланговская функция распределения времени обслуживания Для стационарного режима функционирования СМО с отказами справедливы формулы Эрланга для любых функций распределения времени обслуживания требований. Для большинства СМО суммарное время обслуживания требований образует входящий поток, поэтому его важность для СМО не так существенна, поскольку практически не влияет на ее функционирование. Однако входящий поток сразу становится важным, если он сам является входящим для других приборов. Это многофазовое обслуживание: требование обслуживается последовательно, переходя от одного прибора к другому. Если начальный поток требований пуассоновский, то, проходя последовательно через обслуживающие устройства, поток искажается, постепенно «усиливая» последействие.
Показатели эффективности
Под эффективностью функционирования СМО понимают числовые значения набора показателей (функций), характеризующих уровень выполнения заложенных в нее задач. При анализе функционирования и определении оптимального варианта в качестве параметров используются: n – число приборов (обслуживающих устройств); a - интенсивность входящего потока; b - интенсивность обслуживания требований; l - интенсивность отказов обслуживающего устройства; m - интенсивность восстановления отказавшего устройства; m – число восстанавливающих устройств в системе и др.
1. Показатели эффективности, дающие количественную оценку СМО:
Õ - вероятность того, что в системе все приборы заняты обслуживанием;
A - средняя длина очереди; B - среднее число обслуживаемых требований; À0 – среднее число свободных приборов; Àз - среднее число приборов, занятых обслуживанием; R - среднее число требований в системе;
2. Экономические показатели:
При выборе оптимальных значений параметров СМО экономические показатели могут быть достаточно эффективны. Можно использовать функцию потерь а) для систем с ожиданием
где A – средняя длина очереди, б) для систем с отказами (ограничения на длину очереди)
в) для смешанных систем
Можно применить показатель экономической эффективности системы
где c – экономический эффект, полученный при обслуживании каждого требования в единицу времени,
Примеры моделей СМО
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.225.188 (0.012 с.) |


 . Переход системы из состояния Сi в состояние Сj графически осуществляется по направленным отрезкам с заданными интенсивностями переходов
. Переход системы из состояния Сi в состояние Сj графически осуществляется по направленным отрезкам с заданными интенсивностями переходов  . Если переход невозможен, то
. Если переход невозможен, то 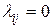 .
.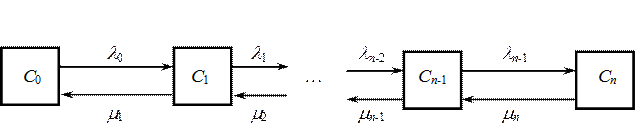
 на оси, разделенных временными интервалами
на оси, разделенных временными интервалами  ,
, 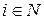 , длина которых случайна.
, длина которых случайна.
 между событиями, по их зависимости или независимости, регулярности и др.
между событиями, по их зависимости или независимости, регулярности и др. (Пирсона) и/или Колмогорова сделать вывод о соответствии или несоответствии выдвинутой гипотезы данной выборке;
(Пирсона) и/или Колмогорова сделать вывод о соответствии или несоответствии выдвинутой гипотезы данной выборке; ,
,  ,
, , то для расчетов либо весь временной интервал
, то для расчетов либо весь временной интервал  разбивается на n временных отрезков, вообще говоря, не равных, и для каждого из них находятся
разбивается на n временных отрезков, вообще говоря, не равных, и для каждого из них находятся 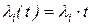 , где
, где  ,
,  , либо используются численные методы. В зависимости от поставленной цели выбирается аналитический подход либо численный.
, либо используются численные методы. В зависимости от поставленной цели выбирается аналитический подход либо численный. поступлений требований (рис. 4.3), образована независимыми случайными величинами
поступлений требований (рис. 4.3), образована независимыми случайными величинами  с функциями распределения
с функциями распределения  ,
,  .
. ) совпадают, то есть,
) совпадают, то есть,  ,
,  ,
,  , то последовательность моментов
, то последовательность моментов  между соседними по времени моментами поступления требований, считаются независимыми случайными величинами.
между соседними по времени моментами поступления требований, считаются независимыми случайными величинами. должны иметь одну и ту же функцию распределения.
должны иметь одну и ту же функцию распределения. ) распределение, является потоком Пальма (очевидно, что последействие здесь имеется).
) распределение, является потоком Пальма (очевидно, что последействие здесь имеется). ,
, 
 .
. .
. между поступлениями соседних требований, являются случайными с функцией распределения Эрланга 2-го порядка и равны
между поступлениями соседних требований, являются случайными с функцией распределения Эрланга 2-го порядка и равны  ,
,  и т.д.
и т.д.
 получаем простейший поток (у него нет последействия). При увеличении k (до 10¸20) получаем поток Пальма с интервалами между поступлениями требований (как показывают многочисленные эксперименты) распределенными практически нормально. При
получаем простейший поток (у него нет последействия). При увеличении k (до 10¸20) получаем поток Пальма с интервалами между поступлениями требований (как показывают многочисленные эксперименты) распределенными практически нормально. При  получаем регулярный (не случайный) поток.
получаем регулярный (не случайный) поток. является важнейшей статистической характеристикой, поскольку определяет пропускную способность СМО. Обычно это случайная величина h с функцией распределения
является важнейшей статистической характеристикой, поскольку определяет пропускную способность СМО. Обычно это случайная величина h с функцией распределения .
. ,
, .
. и обслуживание требования заканчивается, если его обслуживание закончил первый из приборов обслуживания, то функция распределения будет экспоненциальной
и обслуживание требования заканчивается, если его обслуживание закончил первый из приборов обслуживания, то функция распределения будет экспоненциальной .
. , где
, где  ,
,  ,
,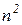 раз.
раз. ,
,  ,
, 
 - вероятность того, что в системе нет требований;
- вероятность того, что в системе нет требований; - вероятность того, что в системе обслуживанием занято k из n приборов;
- вероятность того, что в системе обслуживанием занято k из n приборов; - среднее время, в течение которого любое требование, находящееся в очереди, ждет начала обслуживания;
- среднее время, в течение которого любое требование, находящееся в очереди, ждет начала обслуживания; - вероятность очереди;
- вероятность очереди; - вероятность «потери» требования;
- вероятность «потери» требования; - среднее время пребывания требования в системе, где tср – среднее время обслуживания требования одним прибором;
- среднее время пребывания требования в системе, где tср – среднее время обслуживания требования одним прибором; - коэффициент простоя приборов;
- коэффициент простоя приборов; - коэффициент загрузки системы.
- коэффициент загрузки системы. - стоимость обслуживания каждого требования в системе в единицу времени;
- стоимость обслуживания каждого требования в системе в единицу времени; - стоимость потерь, связанных с простаиванием требований в очереди в единицу времени;
- стоимость потерь, связанных с простаиванием требований в очереди в единицу времени;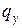 - стоимость потерь, связанных с уходом требования из системы, в единицу времени;
- стоимость потерь, связанных с уходом требования из системы, в единицу времени; - стоимость эксплуатации каждого обслуживающего устройства в единицу времени;
- стоимость эксплуатации каждого обслуживающего устройства в единицу времени; - стоимость простоя обслуживающего устройства в единицу времени.
- стоимость простоя обслуживающего устройства в единицу времени. за определенный временной промежуток T (например, месяц):
за определенный временной промежуток T (например, месяц):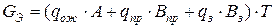 ,
, - среднее число свободных приборов,
- среднее число свободных приборов,  - среднее число занятых приборов;
- среднее число занятых приборов; ;
; .
.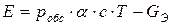 ,
, - вероятность обслуживания требования (для систем с отказами).
- вероятность обслуживания требования (для систем с отказами).


