
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель 2 (системы с ограниченным временем ожидания).Содержание книги
Поиск на нашем сайте
На СМО, состоящую из n приборов, поступает пуассоновский поток требований двух видов на обслуживание интенсивностью Обозначим через В соответствие с моделью имеем размеченный граф состояний системы:
Рис. 4.6 Используя вероятности 1)
где 2)
3)
4)
5)
6)
7)
8)
9)
10) Среднее время нахождение требования в системе:
11)
12)
13)
Пример2. АЗС «Фин-Трейд» имеет четыре заправочных места бензином АИ-92 (две колонки по два заправочных места на каждой). Все автомобили, подъезжающие на АЗС, делятся на 2 типа: - те, кто обязательно дождутся обслуживания, независимо от наличия и величины очереди; - те, кто откажется от заправки из-за наличия очереди. При проведении исследований были выбраны колонки для заправки бензином наиболее востребованной марки - АИ-92 и промежуток времени, когда АЗС испытывает наибольшую нагрузку - с 17 до 21 часа. При помощи применения математического аппарата теории массового обслуживания изучить, насколько эффективно работает АЗС, а именно, заправочные колонки АИ-92, рассчитать и проанализировать следующие показатели эффективности функционирования: - среднее число занятых заправочных мест; - среднее число свободных заправочных мест; - среднее время ожидания автомобилем обслуживания; - вероятность «потери» клиента, вследствие очереди; - среднее время незанятости (простоя) и занятости (загрузки) заправочных мест; - суммарные потери АЗС за исследуемы промежуток времени; Исходные данные: Количество заправочных мест - 4 шт. Промежуток времени для анализа - 4 часа. Среднее число автомобилей - 188 авт./4 часа. Из них: обслужено - 170 авт. не стали обслуживаться - 18 авт. Среднее время обслуживания 1 автомобиля - 5 мин. Автомобиль заправляется в среднем на - 500 руб. Решение. Исходя из постановки задачи, для анализа работы АЗС подходит модель для системы с ограниченным временем ожидания. Определимα1, α2 и β необходимые для расчёта модели. В среднем за 4 часа на АЗС приезжают 190 автомобилей желающих заправиться бензином АИ-92. Все автомобили делятся на 2 типа: 1. Те, кто обязательно дождутся обслуживания независимо от очереди. 2. Те, кто, застав все заправочные места занятыми, откажутся от обслуживания. Приезд автомобилей любого из 2-х видов носит случайный характер. Плотность приезда автомобилей показала, что их поступление на АЗС удовлетворяет пуассоновскому потоку с параметрами α1=170 1/(4 часа) для автомобилей 1-го типа и α2=20 1/(4 часа) для автомобилей 2-го типа. Время обслуживания одного автомобиля (подъезд к заправочному месту, оплата, заправка, отъезд) является случайной величиной, удовлетворяющей экспоненциальному закону со средним временем обслуживания tср=5 мин. Так как для анализа был выбран промежуток размером 4 часа, то интенсивность обслуживания β=48 1/(4 часа). При расчете показателей СМО - работы АЗС с 4-мя заправочными местами для заправки бензином АИ-92 получены следующие результаты: 1) Вероятность того, что на заправочных местах нет автомобилей p0=0,00441. Это означает, что в течение 4-х часов на заправочных местах нет автомобилей ≈ 1 минуту. 2) 3) 4) 5) Вероятность «потери» клиента: 6) Среднее время ожидания обслуживания автомобилем 1-го типа 7) Вероятность того, что время ожидания 8) Среднее число занятых заправочных мест 9) Среднее число свободных заправочных мест 10) Среднее время нахождение автомобиля на АЗС 11) Коэффициент незанятости (простоя) заправочных мест 12) Коэффициент загрузки заправочных мест 13)
Конечно, вряд ли данные расходы соответствуют реально существующим издержкам. Они подойдут только для анализа. Для уменьшения времени ожидания обслуживания и суммарных потерь будем варьировать число заправочных мест 5-х до 7-ти. Результаты расчетов сведем в табл. 4.3: Таблица 4.3
Исходя из полученных данных, можно сделать следующие выводы: 1) Увеличение числа заправочных мест до 5-ти ведет к следующему: - увеличение времени простоя заправочных мест почти в 4 раза; - уменьшение коэффициента загрузки заправочных мест в 1,2 раза; - уменьшение издержек в 1,4 раз; - уменьшение времени ожидания обслуживания почти в 8,5 раза; - вероятность отказа уменьшается в 1,7 раза. 2) При увеличении числа заправочных мест до 6-ти наблюдается: - увеличение времени простоя заправочных мест почти в 6 раз; - уменьшение коэффициента загрузки заправочных мест в 1,4 раза; - уменьшение издержек в 2,3 раз; - уменьшение времени ожидания обслуживания почти в 28 раз; - вероятность отказа уменьшается почти в 4 раза. 3) При увеличении числа заправочных мест до 7-ми так же наблюдаются улучшения некоторых характеристик, но следует отметить что: - вновь увеличиваются издержки; - время простоя заправочных мест увеличилось почти в 8 раз; Выводы. Выгодным (и с экономической точки зрения, и с точки зрения эффективности работы АЗС) является увеличение заправочных мест до 5-ти или 6-ти. Несмотря на то, что мы наблюдаем (в случае работы 6-ти заправочных мест) более значительное, по сравнению с 5-ю заправочными местами, уменьшение издержек, необходимо сделать выбор в пользу увеличения заправочных мест до 5-ти, так как не стоит забывать о следующем: - введение новых заправочных мест ведёт к большим издержкам (расширение площади, оборудование заправочного места) - в случае увеличения числа заправочных мест до 6-ти происходит возрастание времени простоя заправочных мест в 6 раз. - исследования проводились для самого загруженного отрезка времени и то, что времени ожидания обслуживания уменьшается почти в 8,5 раз – это уже хороший показатель, который вместе с уменьшением издержек 1,4 раза и позволяет сделать выбор в пользу увеличения заправочных мест до 5-ти.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.13.192 (0.009 с.) |

 и
и  , соответственно. Поступившее в систему требование 1-го вида может покинуть систему только после обслуживания, а требование 2-го вида, застав все приборы занятыми, сразу покидает систему. Время обслуживания любых требований является случайной величиной, распределенной по экспоненциальному закону с интенсивностью обслуживания b. В любой момент времени каждый прибор может обслуживать не более одного требования. Требуется проанализировать эффективность функционирования СМО.
, соответственно. Поступившее в систему требование 1-го вида может покинуть систему только после обслуживания, а требование 2-го вида, застав все приборы занятыми, сразу покидает систему. Время обслуживания любых требований является случайной величиной, распределенной по экспоненциальному закону с интенсивностью обслуживания b. В любой момент времени каждый прибор может обслуживать не более одного требования. Требуется проанализировать эффективность функционирования СМО. - вероятность того, что в СМО находится k требований (состояние
- вероятность того, что в СМО находится k требований (состояние  ),
), 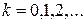 .
.
 получим следующие показатели эффективности функционирования СМО:
получим следующие показатели эффективности функционирования СМО: - вероятность того, что в СМО нет требований:
- вероятность того, что в СМО нет требований: ;
; ,
,  ,
,  ,
,  .
. :
: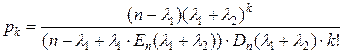 ;
; :
:
 - вероятность очереди, т.е. того, что требований больше чем приборов:
- вероятность очереди, т.е. того, что требований больше чем приборов: ;
; - вероятность «потери» требования:
- вероятность «потери» требования: ;
; - среднее время ожидания обслуживания требованием 1-го типа:
- среднее время ожидания обслуживания требованием 1-го типа: ;
; - вероятность того, что время ожидания
- вероятность того, что время ожидания  требования 1-го типа больше заданного t:
требования 1-го типа больше заданного t: ;
; - среднее число занятых приборов:
- среднее число занятых приборов: ;
; – среднее число свободных приборов
– среднее число свободных приборов ;
; ;
; - коэффициент простоя приборов:
- коэффициент простоя приборов: ;
; - коэффициент загрузки приборов:
- коэффициент загрузки приборов: ;
; - суммарные потери за отчетный период T:
- суммарные потери за отчетный период T: ,
, - упущенная выгода от потери требования в единицу времени;
- упущенная выгода от потери требования в единицу времени; - потери от простоя обслуживающего прибора в единицу времени;
- потери от простоя обслуживающего прибора в единицу времени; - потери, связанные с эксплуатацией прибора в единицу времени.
- потери, связанные с эксплуатацией прибора в единицу времени. - вероятность очереди, т.е. того, что автомобилей больше чем заправочных мест:
- вероятность очереди, т.е. того, что автомобилей больше чем заправочных мест:  . Это означает, что в течение промежутка времени выбранного для исследования (4 часа), число автомобилей на АЗС больше числа заправочных мест ≈ 3 часа 30 минут.
. Это означает, что в течение промежутка времени выбранного для исследования (4 часа), число автомобилей на АЗС больше числа заправочных мест ≈ 3 часа 30 минут. . Это означает, что в течение промежутка времени выбранного для исследования (4 часа), нет свободных заправочных мест ≈ 3 часа 50 минут.
. Это означает, что в течение промежутка времени выбранного для исследования (4 часа), нет свободных заправочных мест ≈ 3 часа 50 минут. . Это означает, что время ожидания обслуживания для каждого автомобиля 1-го типа в среднем ≈ 18 минут.
. Это означает, что время ожидания обслуживания для каждого автомобиля 1-го типа в среднем ≈ 18 минут.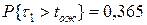 . Это означает, что каждый почти каждый четвёртый автомобиль ожидает больше 18-и минут.
. Это означает, что каждый почти каждый четвёртый автомобиль ожидает больше 18-и минут. .
. .
. 23 минуты.
23 минуты.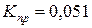 . В среднем каждое заправочное место не занято ≈ 5% времени (время простоя).
. В среднем каждое заправочное место не занято ≈ 5% времени (время простоя). . В среднем каждое заправочное место загружено ≈ 95% времени.
. В среднем каждое заправочное место загружено ≈ 95% времени. ,
, руб.
руб.





