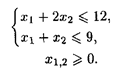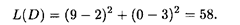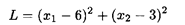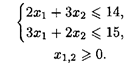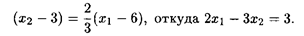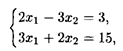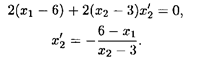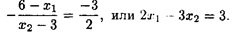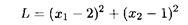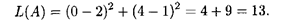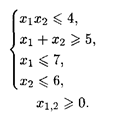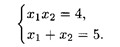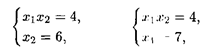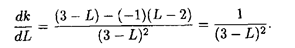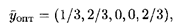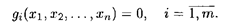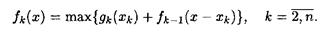Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Нелинейное программированиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ
Управление и планирование являются наиболее сложными функциями в работе предприятий, фирм, служб администраций всех уровней. Долгое время они являлись монополией человека с соответствующей подготовкой и опытом работы. Совершенствование науки, техники, разделение труда усложнили принятие решений в управлении и планировании. Для принятия обоснованного решения необходимо иметь и обработать большое количество информации, определяемое иногда астрономическими цифрами. Принятие ответственных решений, как правило, связано с большими материальными ценностями. В настоящее время недостаточно знать путь, ведущий к достижению цели. Необходимо из всех возможных путей выбрать наиболее экономичный, который наилучшим образом соответствует поставленной задаче. Появление цифровых вычислительных машин и персональных компьютеров создало огромные возможности для развития науки, совершенствования методов планирования и управления производством. Однако без строгих формулировок задач, без математического описания процессов современный уровень управления и планирования не может быть достигнут. Математическая дисциплина, занимающаяся изучением задач управления, планирования и разработкой методов их решения, получила название математического программирования. В данном учебном пособии рассмотрены такие разделы дисциплины как нелинейное, имитационное и стохастическое программирование. В настоящее время не существует общих и достаточно эффективных методов решения задач нелинейного программирования. Лишь для определенного класса нелинейных задач, система ограничений которых линейна, а целевая функция нелинейна, но обладает свойством выпуклости, разработаны достаточно эффективные методы, получившие название методов выпуклого программирования. Динамическое программирование — один из разделов методов оптимизации, в котором процесс принятия решения может быть разбит на отдельные этапы. В основе метода лежит принцип оптимальности, разработанный Р. Беллманом. Сетевые модели, в основе которых лежит теория графов, позволяют проводить их оптимизацию, а также совокупность расчетных и организационных мероприятий по управлению комплексами работ при создании новых изделий и технологий. Цель изучения системы массового обслуживания состоит в том, чтобы контролировать их характеристики для проведения оптимизации системы в целом. Рассмотрение моделей управления запасами преследует цель выбора для предприятий оптимальных расходов на доставку, хранение комплектующих материалов и ресурсов, необходимых для изготовления изделий. Глава 1. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ Общая постановка задачи
Математическая модель задачи нелинейного программирования в общем виде формулируется следующим образом: найти вектор
и доставляющий экстремум (наибольшее или наименьшее значение) целевой функции
где xj — переменные, j = Нелинейное программирование применяется при прогнозировании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудования и т.д. Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, приближенные методы решения, графический метод. Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная. Однако даже для таких задач оптимальное решение может быть найдено для определенного класса целевых функций. Например, когда целевая функция сепарабельная, т.е. является суммой п функций fj(xj), или квадратичная. При этом следует отметить, что в отличие от задач линейного программирования, где точками экстремума являются вершины многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или в вершине. При решении задач нелинейного программирования для целевой функции необходимо определить глобальный максимум или глобальный минимум. Глобальный максимум (минимум) функции — это ее наибольшее (наименьшее) значение из локальных максимумов (минимумов). Наличие локальных экстремумов затрудняет решение задач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найденный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять локальный экстремум, который может существенно отличаться от глобального.
Графический метод
Рассмотрим примеры решения задач нелинейного программирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и нелинейном виде. Так же как и в задачах линейного программирования, они могут быть решены графически.
Задача с линейной целевой функцией и нелинейной системой ограничений
Пример 1. Найти глобальные экстремумы функции
при ограничениях:
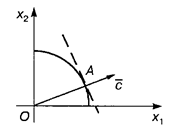
Решение. Область допустимых решений — часть окружности с радиусом 4, которая расположена в первой четверти (рис. 1.1).
Рис. 1.1
Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2. Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем через точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение x 2 = 1/2 х 1. Решаем систему
откуда находим х 1 = 8 Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4 Задача с нелинейной целевой функцией и линейной системой ограничений
Пример 2. Найти глобальные экстремумы функции
при ограничениях:
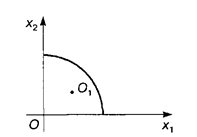
Решение. Область допустимых решений — OABD (рис. 1.2). Линиями уровня будут окружности с центром в
Рис. 1.2
точке O 1. Максимальное значение целевая функция имеет в точке D (9, 0), минимальное — в точке O 1 (2, 3). Поэтому
Ответ. Глобальный максимум, равный 58, достигается в точке D (9, 0), глобальный минимум, равный нулю, — в точке O 1 (2, 3). Пример 3. Найти глобальные экстремумы функции
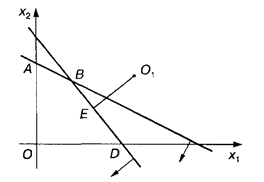
при ограничениях:
Решение. Область допустимых решений — OABD (рис. 1.3). Линии уровня представляют собой окружности с центром в точке O 1 (6, 3). Глобальный максимум находится в точке O (0, 0) как самой удаленной от точки O 1. Глобальный минимум расположен в точке Е, находящейся на пересечении прямой 3 x 1 + 2 x 2 = 15 и перпендикуляра к этой прямой, проведенного из точки O 1.
Рис. 1.3
Найдем координаты точки Е: так как угловой коэффициент прямой 3 x 1 + 2 x 2 = 15 равен -3/2, то угловой коэффициент перпендикуляра O 1 Е равен 2/3. Из уравнения прямой, проходящей через данную точку О 2 с угловым коэффициентом 2/3, получим
Решая систему
находим координаты точки Е: х 1 = 51/13, x 2 = 21/13, при этом L(Е) = 1053/169. Координаты точки Е можно найти следующим образом: дифференцируя выражение (x 1 — 6)2 + (x 2 - 3)2 как неявную функцию по x 1, получим
Приравниваем полученное значение к тангенсу угла наклона прямой 3 x 1 + 2 x 2 = 15:
Решаем систему уравнений
получим координаты точки Е: х 1 = 51/13, x 2 = 21/13. Ответ. Глобальный максимум, равный 52, находится в точке O (0, 0). Глобальный минимум, равный 1053/169, находится в точке E (51/13, 21/13).
Задача с нелинейной целевой функцией и нелинейной системой ограничений
Пример 4. Найти глобальные экстремумы функции
при ограничениях:
Решение. Областью допустимых решений является окружность с радиусом 4, расположенная в первой четверти (рис. 1.4). Линиями уровня будут окружности с центром в точке O 1 (2, l). Глобальный минимум достигается в точке O 1. Глобальный максимум — в точке А (0, 4), при этом
Рис. 1.4
Ответ. Глобальныи минимум, равный нулю, достигается в точке O 1 (2, l), глобальный максимум, равный 13, находится в точке А (0, 4). Пример 5. Найти глобальные экстремумы
при ограничениях:
Решение. Область допустимых решений не является выпуклой и состоит из двух частей (рис. 1.5). Линиями уровня являются окружности с центром в точке O (0, 0).
Рис. 1.5
Найдем координаты точек А и В, решая систему
Получим А (1, 4), В (4, 1). В этих точках функция имеет глобальные минимумы, равные 17. Найдем координаты точек D и Е, решая системы
откуда получаем D (2/3, 6) и L(D) = 328/9, E (7, 4/7) и L(E) = 2417/49. Ответ. Целевая функция имеет два глобальных минимума, равных 17, в точках А (1, 4) и B (4, 1), глобальный максимум, равный 2417/49, достигается в точке E (7, 4/7). Рис. 1.6 Установим, как будет вести себя угловой коэффициент k при монотонном возрастании L. Найдем производную от k по L:
Знаменатель производной всегда положителен, а числитель от L не зависит. Следовательно, производная имеет постоянный знак и при увеличении L угловой коэффициент будет только возрастать или только убывать, а прямая будет поворачиваться в одну сторону. Если угловой коэффициент прямой имеет положительное значение, то прямая вращается против часовой стрелки, при отрицательном значении k — по часовой стрелке. Установив направление вращения, находим вершину или вершины многогранника, в которых функция принимает max(min) значение, либо устанавливаем неограниченность задачи. При этом возможны следующие случаи. 1. Область допустимых решений ограничена, максимум и минимум достигаются в ее угловых точках (рис. 1.7). 2. Область допустимых решений неограничена, однако существуют угловые точки, в которых целевая функция принимает максимальное и минимальное значения (рис. 1.8). 3. Область допустимых решений неограничена, имеется один из экстремумов. Например, минимум достигается в одной из вершин области и имеет так называемый асимптотический максимум (рис. 1.9). 4. Область допустимых решений неограничена. Максимум и минимум являются асимптотическими (рис. 1.10).
Алгоритм решения
1. Находим область допустимых решений. 2. Определяем угловой коэффициент k и устанавливаем направление поворота целевой функции. 3. Находим точку max(min) целевой функции или устанавливаем неразрешимость задачи.
Экономическая интерпретация задач дробно-линейного программирования
Математическая модель задачи дробно-линейного программирования может быть использована для определения рентабельности затрат на производство изделий, рентабельности продаж, затрат в расчете на рубль выпускаемой продукции, себестоимости изделий. Обозначим: rj — прибыль предприятия от реализации единицы изделия j -гo вида; xj — количество выпущенной продукции j- гo вида; sj — цена единицы продукции j- гo вида; cj — себестоимость производства единицы изделия j- гoвида; dj — затраты на производство одного изделия j -гo вида. Задача рентабельности (Р з) затрат на производство изделий имеет вид
Задача рентабельности (Рn) продаж имеет вид
Задача определения затрат (З р) в расчете на рубль товарной продукции записывается в виде
Задача нахождения себестоимости изделия записывается как
Указанные математические модели имеют системы ограничений в зависимости от условий задачи.
Применение дробно-линейного программирования для определения себестоимости изделий
Рассмотрим использование дробно-линейного программирования для нахождении себестоимости изделий. Пример 6. Для производства двух видов изделий А и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в табл. 1.1 Оборудование I и III типов предприятие может использовать не более 26 и 39 ч соответственно, оборудование II типа целесообразно использовать не менее 4 ч. Определить, сколько изделий каждого вида следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.
Таблица 1.1
Решение. Составим математическую модель задачи. Пусть x 1 — количество изделий вида А, которое следует изготовить предприятию, x 2 — количество изделий вида В. Общие затраты на их производство составят (2 х 1 + 3 x 2) тыс. р., а средняя себестоимость одного изделия будет равна
Математическая модель задачи примет вид
при ограничениях:
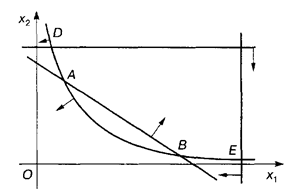
Δ АВС — область допустимых решений (рис. 1.11).
Рис. 1.11
Найдем x 2: L = (2 x 1 + 3 x 2) / (x 1 + x 2), 2 x 1 + 3 х 2 = Lx 1 + Lx 2, x 2 (3 - L) = x 1(L - 2),
Угловой коэффициент прямой равен k = (L - 2)/(3 — l), тогда
Так как dk/dL > 0, то функция k = (L - 2)/(3 - L) возрастает. Это соответствует вращению прямой против часовой стрелки. Следовательно, в точке С (рис. 1.11) целевая функция будет иметь наименьшее значение (глобальный минимум). Найдем координаты точки С. Решая систему
получим С (3, 1), Следовательно, предприятию следует выпускать 3 изделия вида А и 1 изделие вида В. При этом средняя себестоимость одного изделия будет минимальной и равной 2,25 тыс. р.
Сведение экономико-математической модели дробно-линейного программирования к задаче линейного программирования
Задачу дробно-линейного программирования можно свести к задаче линейного программирования и решить симплексным методом. Обозначим
при условии
и введем новые переменные уj = y 0 xj. Тогда задача примет вид
при ограничениях:
После нахождения оптимального решения полученной задачи, используя вышеуказанные соотношения, найдем оптимальное решение исходной задачи дробно-линейного программирования. Пример 7. Дана задача дробно-линейного программирования
при ограничениях:
Решение. Обозначим: x 1 + 2 x 2 + 1 = 1/ у 0, y 0 > 0, тогда L = 2 x 1 y 0 - x2y 0. Обозначим: x 1 y 0 = y 1, х 2 у 0 = у 2, х 3 у 0 = у 3, х 4 у 0 = y 4. Преобразуем систему ограничений, умножив обе части всех ограничений на у 0, и перейдем к переменным у 0, y 1, y 2, y 3, y 4. Задача примет вид
при ограничениях:
Таблица 1.2
Получили задачу линейного программирования, решаем ее симплексным методом (табл. 1.2). Получим
тогда
Ответ:
Метод множителей Лагранжа Постановка задачи
Дана задача нелинейного программирования
при ограничениях:
Предположим, что функции f (x 1, х 2 ,..., xп) и gi(x 1, x 2,..., xп) непрерывны вместе со своими первыми частными производными. Ограничения заданы в виде уравнений, поэтому для решения задачи воспользуемся методом отыскания условного экстремума функции нескольких переменных. Для решения задачи составляется функция Лагранжа
где λ i — множители Лагранжа. Затем определяются частные производные:
Приравняв к нулю частные производные, получим систему
Решая систему, получим множество точек, в которых целевая функция L может иметь экстремальные значения. Следует отметить, что условия рассмотренной системы являются необходимыми, но недостаточными. Поэтому не всякое полученное решение определяет точку экстремума целевой функции. Применение метода бывает оправданным, когда заранее предполагается существование глобального экстремума, совпадающего с единственным локальным максимумом или минимумом целевой функции. Пример 8. Найти точку условного экстремума функции
при ограничениях:
Решение. Составим функцию Лагранжа
Найдем частные производные функции Лагранжа по переменным x 1, x 2, x 3, λ1, λ2. Приравняв к нулю полученные выражения, решим систему
Откуда λ1 = - x 2, λ2 = - x 2/2, х 1 = -2, x 2 = -4, x 3 = 4, L = -8. Определим характер экстремума, изменяя полученные значения переменных. Измененные значения должны удовлетворять заданной системе ограничений. Возьмем х 1 > -2, например x 1 = -1, тогда из системы ограничений получим х 2 = -3, x 3 = 7/2, L = -15/2. Возьмем х 1 < -2, например х 1 = -3, тогда получим х 2 = -5, x 3 = 9/2, L = -15/2. Следовательно, L = -8 — минимальное значение функции. Ответ. Точка экстремума х 1 = -2, x 2 = -4, x 3 = 4, при этом максимальное значение функции L = -8.
Расчет экономико-математической модели при нелинейных реализациях продукции
Рассмотрим применение выше приведенных методов на примере решения задачи оптимальной реализации продукции. Пример 9. Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов. При продаже x 1 кг муки через магазин расходы на реализацию составляют х 12 ден. ед., а при продаже x 2 кг муки посредством торговых агентов — х 22 ден. ед. Определить, сколько килограммов муки следует продавать каждым способом, чтобы затраты на реализацию были минимальными, если в сутки выделяется для продажи 5 000 кг муки. Решение. Составим математическую модель задачи. Найдем минимум суммарных расходов
при ограничениях:
Для расчета модели используем метод множителей Лагранжа. Составим функцию Лагранжа
Найдем частные производные функции F по x 1, x 2 и λ, приравняем их к нулю, получим систему уравнений
откуда λ = -5 000, x 1 = 2 500, x 2 = 2 500, L = 12 500 000 ден. ед. Давая х 1 значения больше и меньше 2500, находим L и из определения экстремума функции получаем, что L при х 1 = x 2 = 2 500 достигает минимума. Таким образом, для получения минимальных расходов необходимо расходовать в сутки через магазин и торговых агентов по 2 500 кг муки, при этом расходы на реализацию составят 12 500 000 ден. ед.
Постановка задачи
Динамическое программирование — один из разделов оптимального программирования, в котором процесс принятия решения и управления может быть разбит на отдельные этапы (шаги). Экономический процесс является управляемым, если можно влиять на ход его развития. Под управлением понимается совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса. Например, выпуск продукции предприятием — управляемый процесс. Совокупность решений, принимаемых в начале года (квартала и т.д.) по обеспечению предприятия сырьем, замене оборудования, финансированию и т.д., является управлением. Необходимо организовать выпуск продукции так, чтобы принятые решения на отдельных этапах способствовали получению максимально возможного объема продукции или прибыли. Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения. В отличие от линейного программирования, в котором симплексный метод является универсальным методом решения, в динамическом программировании такого универсального метода не существует. Одним из основных методов динамического программирования является метод рекуррентных соотношений, который основывается на использовании принципа оптимальности, pазработанного американским математиком Р. Беллманом. Принцип состоит в том, что, каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага. Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом. В некоторых задачах, решаемых методом динамического программирования, процесс управления разбивается на шаги. При распределении на несколько лет ресурсов деятельности предприятия шагом целесообразно считать временной период; при распределении средств между предприятиями — номер очередного предприятия. В других задачах разбиение на шаги вводится искусственно. Например, непрерывный управляемый процесс можно рассматривать как дискретный, условно разбив его на временные отрезки (шаги). Исходя из условий каждой конкретной задачи, длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.
Рис. 2.1 Функциональные уравнения, основанные на принципе оптимальности, имеют вид:
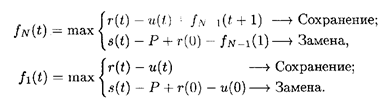
Уравнение (2.1) описывает N -стадийный процесс, а (2.2) — одностадийный. Оба уравнения состоят из двух частей: верхняя строка определяет доход, получаемый при сохранении оборудования; нижняя — доход, получаемый при замене оборудования и продолжении процесса работы на новом оборудовании. В уравнении (2.1) функция r(t) — u(t) есть разность между стоимостью произведенной продукции и эксплуатационными издержками на N- й стадии процесса. Функция fN- 1 (t + 1) характеризует суммарную прибыль от (N — 1) оставшихся стадий для оборудования, возраст которого в начале осуществления этих стадий составляет (t + 1) лет. Нижняя строка (2.1) характеризуется следующим образом: функция s(t) — Р представляет чистые издержки по замене оборудования, возраст которого t лет. Функция r (0) выражает доход, получаемый от нового оборудования возраста 0 лет. Предполагается, что переход от работы на оборудовании возраста t лет к работе на новом оборудовании совершается мгновенно, т.е. период замены старого оборудования и переход на работу на новом оборудовании укладываются в одну и ту же стадию. Последняя функция fN- 1 в (2.1) представляет собой доход от оставшихся N — 1 стадий, до начала осуществления которых возраст оборудования составляет один год. Аналогичная интерпретация может быть дана уравнению для одностадийного процесса. Здесь нет слагаемого вида f 0 (t + 1), так как N принимает значение 1, 2,..., N. Равенство f 0 (t) = 0 следует из определения функции fN(t). Уравнения (2.1) и (2.2) являются рекуррентными соотношениями, которые позволяют определить величину fN(t) в зависимости от fN -1(t + 1). Структура этих уравнений показывает, что при переходе от одной стадии процесса к следующей возраст оборудования увеличивается с t до (t + 1) лет, а число оставшихся стадий уменьшается с N до (N — 1). Расчет начинают с использования уравнения (2.1). Уравнения (2.1) и (2.2) позволяют оценить варианты замены и сохранения оборудования, с тем чтобы принять тот из них, который предполагает больший доход. Эти соотношения дают возможность не только выбрать линию поведения при решении вопроса о сохранении или замене оборудования, но и определить прибыль, получаемую при принятии каждого из этих решений. Пример 1. Определить оптимальный цикл замены оборудования при следующих исходных данных: Р = 10, S(t) = 0, f(t) = r(t) — u(t), представленных в табл. 2.1. Таблица 2.1
Решение. Уравнения (2.1) и (2.2) запишем в следующем виде:
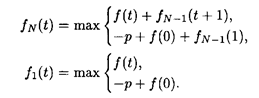
Для N = 1
Для N = 2
Вычисления продолжаем до тех пор, пока не будет выполнено условие f 1(1) > f 2(2), т.е. в данный момент оборудование необходимо заменить, так как величина прибыли, получаемая в результате замены оборудования, больше, чем в случае использования старого. Результаты расчетов помещаем в таблицу, момент замены отмечаем звездочкой, после чего дальнейшие вычисления по строчке прекращаем (табл. 2.2). Таблица 2.2
Можно не решать каждый раз уравнение (2.3), а вычисления проводить в таблице. Например, вычислим f 4 (t):
Дальнейшие расчеты для f 4 (t) прекращаем, так как f 4(4) = 23 < f 3(1) = 24. По результатам вычислений и по линии, разграничивающей области решений сохранения и замены оборудования, находим оптимальный цикл замены оборудования. Для данной задачи он составляет 4 года. Ответ. Для получения максимальной прибыли от использования оборудования в двенадцатиэтапном процессе оптимальный цикл состоит в замене оборудования через каждые 4 года.
Оптимальное распределение ресурсов
Пусть имеется некоторое количество ресурсов х, которое необходимо распределить между п различными предприятиями, объектами, работами и т.д. так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Введем обозначения: xi — количество ресурсов, выделенных i -му предприятию (i = gi(xi) — функция полезности, в данном случае это величина дохода от использования ресурса xi, полученного i- м предприятием; fk(x) — наибольший доход, который можно получить при использовании ресурсов х от первых k различных предприятий. Сформулированную задачу можно записать в математической форме:
при ограничениях:
Для решения задачи необходимо получить рекуррентное соотношение, связывающее fk(x) и fk- 1 (x). Обозначим через хk количество ресурса, используемого k- мспособом (0 ≤ xk ≤ х), тогда для (k — 1) способов остается величина ресурсов, равная (x — xk). Наибольший доход, который получается при использовании ресурса (x — xk) от первых (k — 1 ) способов, составит fk- 1 (x — xk). Для максимизации суммарного дохода от k- гo и первых (k — 1) способов необходимо выбрать xk таким образом, чтобы выполнялись соотношения
Рассмотрим конкретную задачу по распределению капиталовложений между предприятиями.
Распределение инвестиций для эффективного использования потенциала предприятия
Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме. Для расширения производства совет директоров выделяет средства в объеме 120 млн р. с дискретностью 20 млн р. Прирост выпуска продукции на предприятиях зависит от выделенной суммы, его значения представлены предприятиями и содержатся в табл. 2.3. Найти распределение средств между предприятиями, обеспечивающее максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить не более одной инвестиции.
Таблица 2.3
Решение. Разобьем решение задачи на четыре этапа по количеству предприятий, на которых предполагается осуществить инвестиции. Рекуррентные соотношения будут иметь вид: для предприятия № 1
для всех остальных предприятий
Решение будем проводить согласно рекуррентным соотношениям в четыре этапа. 1-й этап. Инвестиции производим только первому предприятию. Тогда
2-й этап. Инвестиции выделяем первому и второму предприятиям. Рекуррентное соотношение для 2-го этапа имеет вид
Тогда при х = 20 f 2(20) = max (8 + 0,0 + 10) = max (8, 10) = 10, при x = 40 f 2(40) = max (16,8 + 10,20) = max (16, 18, 20) =20, при х = 60 f 2(60) = max (25,16 + 10, 8 + 20,28) = max (25,26, 28,28) =28, при х = 80 f 2(80) = max (36,25 + 10,16 + 20,8 + 28,40) = max (36, 35, 36, 36, 40) = 40, при х = 100 f 2(100) = max (44,36 + 10,25 + 20,16 + 28,8 + 40,48) = max (44, 46, 45, 44, 48, 48) = 48, при х = 120 f 2(120) = max (62,44 + 10,36 +20,25 + 28,16 + 40,8 + 48,62) = max (62, 54, 56, 53, 56, 56, 62) = 62. 3-й этап. Финансируем 2-й этап и третье предприятие. Расчеты проводим по формуле
Тогда при х = 20 f 3(20) = mах (10, 12) = 12, при x = 40 f 3(40) = max (20,10 + 12,21) = max (20, 22, 21) = 22, при х = 60 f 3(60) = max (28,20 + 12,10 + 21,27) = max (28, 32, 31, 27) = 32, при х = 80 f 3(80) = max (40,28 + 12,20 + 21,10 + 27,38) = max (40, 40, 41, 37, 38) = 41, при x = 100 f 3(100) = max (48,40 + 12,28 + 21,20 + 27,10 + 38,50) = max (48, 52, 49, 47, 48, 50) = 52, при х = 120 f 3(120) = max (62,48 + 12,40 + 21,28 + 27,20 + 38,10 + 50,63) = max (62, 60, 61, 55, 58, 60, 63) = 63. 4-й этап. Инвестиции в объеме 120 млн р. распределяем между 3-м этапом и четвертым предприятием. При х = 120 f 4(120) = max (63,52 + 11,41 + 23,32 + 30,22 + 37,12 + 51,63) = max (63, 63, 64, 62, 59, 63, 63) = 64.
|
||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 6490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.193.166 (0.011 с.) |

 = (х 1, x 2, …, xn), удовлетворяющий системе ограничений
= (х 1, x 2, …, xn), удовлетворяющий системе ограничений
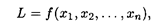
 ; L, f, gi — заданные функции от n переменных, bi — фиксированные значения.
; L, f, gi — заданные функции от n переменных, bi — фиксированные значения.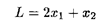
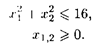
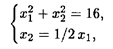
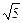 /5, x 2 = 4
/5, x 2 = 4