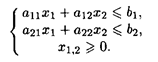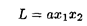Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение экономических задач с использованием моделей управления запасамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Решим задачу с применением основной модели управления запасами. Пример 1. Интенсивность равномерного спроса составляет 2000 телевизоров в год. Организационные издержки для одной партии составляют 20 тыс. р. Цена единицы товара равна 1 тыс. р., а издержки содержания телевизоров составляют 0,1 тыс. р. за один телевизор в год. Найти оптимальный размер партии, число поставок и продолжительность цикла. Решение. По условию задачи g = 2000, b = 20, s = 1, h = 0,1. Общие издержки в течение года:
Ответ. Оптимальный размер партии составляет 894 телевизора, число поставок — 2,24, продолжительность цикла — 163 дня. Рассмотрим задачу с применением модели производственных поставок. Пример 2. Интенсивность равномерного спроса выпускаемых фирмой видеомагнитофонов составляет 2000 шт. в год. Организационные издержки равны 20 тыс. р. Цена видеомагнитофона составляет 1 тыс. р., издержки хранения равны 0,1 тыс. р. в расчете на один видеомагнитофон в год. Запасы на складе пополняются со скоростью 4000 видеомагнитофонов в год. Производственная линия начинает действовать, как только уровень запасов на складе становится равным нулю, и продолжает работу до тех пор, пока не будет произведено q видеомагнитофонов. Найти размер партии, который минимизирует все затраты. Определить число поставок в течение года, время, в течение которого продолжается поставка, продолжительность цикла, максимальный уровень запасов и средний уровень запасов при условии, что размер поставки оптимален. Решение. Данная модель задачи является моделью производственных поставок со следующими параметрами:
График изменения запасов представлен на рис. 5.6.
Рис. 5.6 Число партий в течение года:
Продолжительность поставки:
Продолжительность цикла:
Максимальный уровень запасов:
Средний уровень запасов:
Уравнение издержек:
Решив уравнение dC/dq = 0, получим q опт = Найдем оптимальные значения поставок, продолжительность поставки, продолжительность цикла:
Ответ. За каждую поставку необходимо доставлять на склад 1265 видеомагнитофонов, оптимальное число поставок составляет 1,6, продолжительность поставки — 115 дней, продолжительность цикла — 230 дней.
СПИСОК ЛИТЕРАТУРЫ
1. Красс, М. С. Основы математики и ее приложения в экономическом образовании // учебник / М. С. Красс, Б. П. Чупрынов. - 4-е изд., испр.. - М.: Дело, 2003. - 688 с. - 5000 экз. - ISBN 5-7749-0186-6 (в пер.). 2. Павский, В. А. Теория массового обслуживания // учеб. пособие для студ. вузов / В. А. Павский. - Кемерово: КемТИПП, 2008. - 116 с. - 600 экз. - ISBN 978-5-89289-513-2. 3. Макаров С.И. Экономико-математические методы и модели. // Учебное пособие, 2009, КноРус, 241 c., ISBN: 978-5-390-00451-7. 4. Колокольцов В. Н., Малафеев О. А. Математическое моделирование многоагентных систем конкуренции и кооперации (Теория игр для всех) // 1-е изд., 2012. - 624 с. - ISBN 978-5-8114-1276-1. 5. Орлова И. В. Экономико-математическое моделирование. // практич. пособие, 2012, ISBN: 978-5-9558-0107-0. 6. Бережная, Е. В. Математические методы моделирования экономических систем // учеб. пособие для студ. вузов / Е. В. Бережная, В. И. Бережной. - 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2006. - 431 с. - 2000 экз. - ISBN 5-279-02940-8 7. Кудрявцев Е. М. Методы сетевого планирования и управления проектом. // Учебное пособие, 2008, ДМК Пресс, 239 c, ISBN: 5-94074-187-8. КОНТРОЛЬНЫЕ ЗАДАНИЯ
Выполняется одна контрольная работа (задания 1 - 12), вариант следует выбирать по последней цифре номера зачетной книжки. Если номер заканчивается 0, то он соответствует 10 варианту. Не следует приступать к выполнению контрольных работ, не изучив соответствующих разделов и не разобрав приведенных в них примеров. Возникшие вопросы можно задать связавшись с кафедрой (vm@kemtipp.ru). Контрольные работы оформляются в отдельной тетради, оставляя поля для замечаний рецензента, либо в отдельном файле (в названии файла должны быть указаны предмет, город, группа, ФИО студента), если Ваш населенный пункт расположен в ином городе, чем сам ВУЗ, в котором Вы обучаетесь. Условие задачи должно быть переписано полностью. Решение выполняется в логической последовательности с пояснениями и краткими формулировками производимых действий. Выполненные контрольные работы студентом доставляются в институт или отправляются по электронной почте на рецензирование (vm@kemtipp.ru). Получив проверенную работу, студенту необходимо исправить отмеченные ошибки и, если она не зачтена, выслать на повторное рецензирование. Контрольные работы, выполненные небрежно, без соблюдения предъявляемых требований или не своего варианта, не рассматриваются.
1. Задания по теме "Нелинейное программирование"
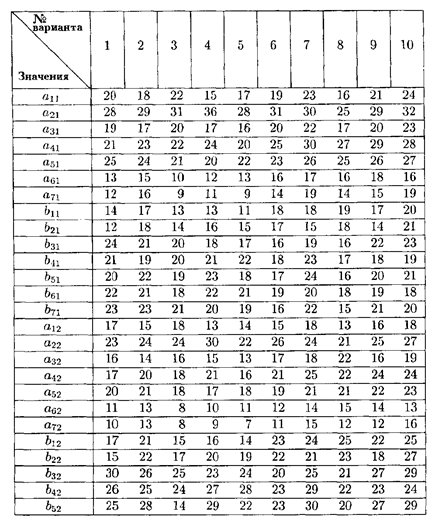
Задание 1. Дана задача с нелинейной целевой функцией и линейной системой ограничений. Используя графический метод, найти глобальные экстремумы функции
при ограничениях:
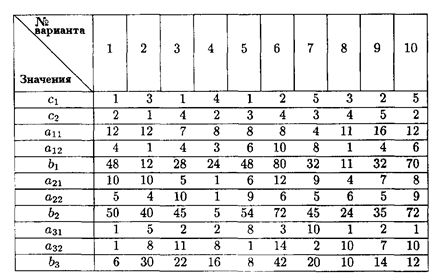
Значения коэффициентов целевой функции и системы ограничений
Задание 2. Решить задачу дробно-линейного программирования. Для производства двух изделий A и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на данном типе оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в таблице. Оборудование 1-го и 3-го типов предприятие может использовать не менее b 1 и b 3 ч соответственно, оборудование 2-го типа — не более b 2 ч. Определить, сколько изделий следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.
Значения коэффициентов условия задачи
Задание 3. Дана задача нелинейного программирования
при ограничении
Найти условный экстремум с использованием метода множителей Лагранжа.
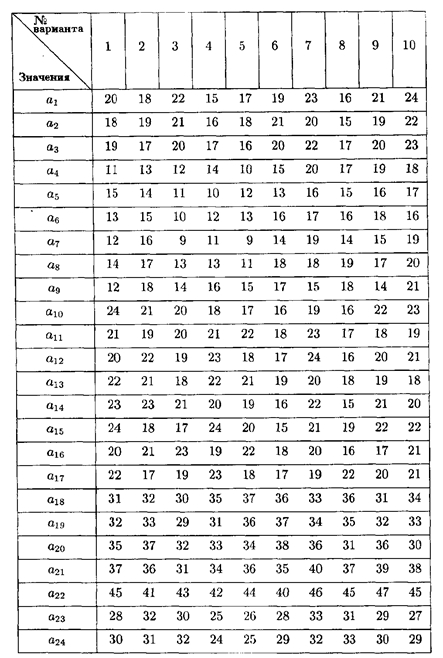
Значения коэффициентов целевой функции и системы ограничений
2. Задания по теме "Динамическое программирование"
Задание 4. Определить оптимальный цикл замены оборудования при следующих исходных данных: S(t) = 0, f(t) = r(t) — u(t).
Значения коэффициентов условия задачи
Задание 5. Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме. Для модернизации предприятий совет директоров инвестирует средства в объеме 250 млн р. с дискретностью 50 млн р. Прирост выпуска продукции зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таблице. Найти распределение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить только одну инвестицию.
Значения коэффициентов условия задачи
Задание 6. В трех районах города предприниматель планирует строительство пользующихся спросом одинаковых по площади мини-магазинов "Продукты". Известны места, в которых их можно построить. Подсчитаны затраты на их строительство и эксплуатацию. Необходимо так разместить мини-магазины, чтобы затраты на их строительство и эксплуатацию были минимальные.
Значения коэффициентов условия задачи
3. Задания по теме "Сетевые модели"
Задание 7. Районной администрацией принято решение о газификации одного из небольших сел района, имеющего 10 жилых домов. Расположение домов указано на рис. 1. Числа в кружках обозначают условный номер дома. Узел 11 является газопонижающей станцией.
Рис. 1
Разработать такой план газификации села, чтобы общая длина трубопроводов была наименьшей. Значения коэффициентов условия задачи
Задание 8. Транспортному предприятию требуется перевезти груз из пункта 1 в пункт 14. На рис. 2 показана сеть дорог и стоимость перевозки единицы груза между отдельными пунктами.
Рис. 2
Определить маршрут доставки груза, которому соответствуют наименьшие затраты. Значения коэффициентов условия задачи
Задание 9. Составить сетевой график выполнения работ и рассчитать временные параметры по данным, представленным в таблице.
Значения коэффициентов условия задачи
Задание 10. Постройте график работ, определите критический путь и стоимость работ до сжатия. Найдите критический путь и минимальную стоимость работ после сжатия.
Значения коэффициентов условия задачи
4. Задания по теме "Система массового обслуживания"
Задание 11. Приходная касса городского района с временем работы А часов в день проводит прием от населения коммунальных услуг и различных платежей в среднем от В человек в день. В приходной кассе работают С операторов-кассиров. Средняя продолжительность обслуживания одного клиента составляет D мин. Определить характеристики работы приходной кассы как объекта СМО.
Задание 12. Салон парикмахерских услуг имеет А мест для обслуживания клиентов. Среднее время обслуживания одного клиента - D мин. В среднем за рабочую смену (8 часов) салон посещает B потенциальных клиентов. Из них, в среднем, С клиентов отказывается от услуг из-за отсутствия свободных мастеров. 1. Требуется изучить, насколько эффективно работает салон-парикмахерская, рассчитать и проанализировать следующие показатели эффективности функционирования салона: - вероятность простоя салона; - среднее число занятых специалистов-парикмахеров; - среднее число свободных специалистов; - вероятность очереди, т.е. того, что клиентов больше чем специалистов; - среднее время ожидания клиентом обслуживания; - вероятность «потери» клиента, вследствие очереди; - среднее время незанятости (простоя) и занятости (загрузки) специалистов; 2. Рассчитать показатели эффективности функционирования салона для (А+1) и (А+2) рабочего места (результаты представить в виде таблицы). Проанализировать, является ли целесообразным увеличение числа рабочих мест в салоне. Сделать выводы.
Значения коэффициентов условия задачи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.009 с.) |




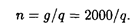

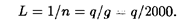



 = 1265 видеомагнитофонов.
= 1265 видеомагнитофонов.