
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель 5 (замкнутые системы, синтез).
Имеется непрерывно работающий прибор, состоящий из m модулей. В процессе работы прибора модули могут выходить из строя в случайные моменты времени. Время наработки машины на отказ является случайной величиной с экспоненциальной функцией распределения и параметром В случае выхода модуля из строя он мгновенно заменяется одним из n запасных, если таковой имеется, иначе прибор останавливается. Вышедший из строя модуль попадает в ремонт, где восстанавливается одним из r восстанавливающих устройств (операторов). Время восстановления является случайной величиной с экспоненциальной функцией распределения и интенсивностью восстановления Пусть
из которого получаем систему однородных алгебраических уравнений:
Условие нормировки, являющееся следствием модели, имеет вид:
Решая систему (с учетом условия нормировки), получаем:
Вычислим показатели эффективности, исходя из найденных вероятностей: 1)
2)
3)
4)
5)
6) M - среднее число модулей, ожидающих ремонта:
Для определения экономически целесообразного числа запасных модулей и числа восстанавливающих устройств (операторов) воспользуемся формулой, минимизирующей потери при эксплуатации прибора:
где
Если число восстанавливающих устройств фиксировано, то
определяет оптимальное число запасных модулей (обеспечивающих минимум потерь из-за простоя прибора и затрат на покупку запасных модулей). Модель может быть использована для анализа и синтеза ненадежных систем, состоящих из большого числа однотипных элементов: вычислительные системы; парк автобусов, трамваев; предприятия общественного питания и магазины бытовой техники (планирование необходимого количества запасных частей для продажи, сервисных центров и т.д.).
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.253.170 (0.004 с.) |
 ,
,  - среднее время работы машины до отказа.
- среднее время работы машины до отказа. ,
,  - среднее время восстановления одного модуля. Восстановленные модули возвращаются в резерв. Требуется оценить эффективность работы прибора.
- среднее время восстановления одного модуля. Восстановленные модули возвращаются в резерв. Требуется оценить эффективность работы прибора. - вероятность того, что в приборе k неисправных модулей (состояние
- вероятность того, что в приборе k неисправных модулей (состояние  ),
), 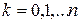 , а
, а  - вероятность того, что прибор не может работать (отсутствуют исправные модули для замены вновь вышедшего – состояние
- вероятность того, что прибор не может работать (отсутствуют исправные модули для замены вновь вышедшего – состояние  ). Построим размеченный граф возможных состояний прибора (рис. 4.9),
). Построим размеченный граф возможных состояний прибора (рис. 4.9), Рис. 4.9
Рис. 4.9 ,
, ,
,  ,
, ,
,  ,
, .
. .
. ;
; ,
,  ;
; ,
,  .
. - вероятность того, что все n занятых модулей прибора в исправном состоянии;
- вероятность того, что все n занятых модулей прибора в исправном состоянии; - вероятность того, что прибор не будет работать;
- вероятность того, что прибор не будет работать;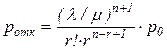 ;
; – среднее число модулей, находящихся в ремонте, при бесперебойной работе прибора:
– среднее число модулей, находящихся в ремонте, при бесперебойной работе прибора: ;
; - среднее число операторов занятых восстановлением модулей:
- среднее число операторов занятых восстановлением модулей: ;
; - коэффициент загрузки операторов:
- коэффициент загрузки операторов: ;
; .
. ,
, - стоимость запасных модулей;
- стоимость запасных модулей; - стоимость содержания одного восстанавливающего устройства в единицу времени;
- стоимость содержания одного восстанавливающего устройства в единицу времени; - стоимость простоя прибора в единицу времени;
- стоимость простоя прибора в единицу времени; - среднее время работы запасного модуля.
- среднее время работы запасного модуля. . Тогда формула
. Тогда формула



