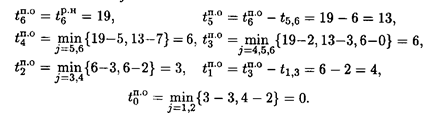Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые экономические задачи, решаемые методами динамичес-кого программированияСодержание книги
Поиск на нашем сайте
Оптимальная стратегия замены оборудования
Одной из важных экономических проблем является определение оптимальной стратегии в замене старых станков, агрегатов, машин на новые. Старение оборудования включает его физический и моральный износ, в результате чего растут производственные затраты по выпуску продукции на старом оборудовании, увеличиваются затраты на его ремонт и обслуживание, снижаются производительность и ликвидная стоимость. Наступает время, когда старое оборудование выгоднее продать, заменить новым, чем эксплуатировать ценой больших затрат; причем его можно заменить новым оборудованием того же вида или новым, более совершенным. Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены. Критерием оптимальности при этом может служить прибыль от эксплуатации оборудования, которую следует оптимизировать, или суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации. Введем обозначения: r(t) — стоимость продукции, производимой за один год на единице оборудования возраста t лет; u(t) — ежегодные затраты на обслуживание оборудования возраста t лет; s(t) — остаточная стоимость оборудования возраста t лет; Р — покупная цена оборудования. Рассмотрим период N лет, в пределах которого требуется определить оптимальный цикл замены оборудования. Обозначим через fN(t) максимальный доход, получаемый от оборудования возраста t лет за оставшиеся N лет цикла использования оборудования при условии оптимальной стратегии. Возраст оборудования отсчитывается в направлении течения процесса. Так, t = 0 соответствует случаю использования нового оборудования. Временные же стадии процесса нумеруются в обратном направлении по отношению к ходу процесса. Так, N = 1 относится к одной временной стадии, остающейся до завершения процесса, а N = N — к началу процесса (рис. 2.1). На каждом этапе N -стадийного процесса должно быть принято решение о сохранении или замене оборудования. Выбранный вариант должен обеспечивать получение максимальной прибыли.
Рис. 2.1 Функциональные уравнения, основанные на принципе оптимальности, имеют вид:
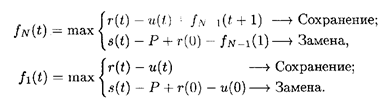
Уравнение (2.1) описывает N -стадийный процесс, а (2.2) — одностадийный. Оба уравнения состоят из двух частей: верхняя строка определяет доход, получаемый при сохранении оборудования; нижняя — доход, получаемый при замене оборудования и продолжении процесса работы на новом оборудовании. В уравнении (2.1) функция r(t) — u(t) есть разность между стоимостью произведенной продукции и эксплуатационными издержками на N- й стадии процесса. Функция fN- 1 (t + 1) характеризует суммарную прибыль от (N — 1) оставшихся стадий для оборудования, возраст которого в начале осуществления этих стадий составляет (t + 1) лет. Нижняя строка (2.1) характеризуется следующим образом: функция s(t) — Р представляет чистые издержки по замене оборудования, возраст которого t лет. Функция r (0) выражает доход, получаемый от нового оборудования возраста 0 лет. Предполагается, что переход от работы на оборудовании возраста t лет к работе на новом оборудовании совершается мгновенно, т.е. период замены старого оборудования и переход на работу на новом оборудовании укладываются в одну и ту же стадию. Последняя функция fN- 1 в (2.1) представляет собой доход от оставшихся N — 1 стадий, до начала осуществления которых возраст оборудования составляет один год. Аналогичная интерпретация может быть дана уравнению для одностадийного процесса. Здесь нет слагаемого вида f 0 (t + 1), так как N принимает значение 1, 2,..., N. Равенство f 0 (t) = 0 следует из определения функции fN(t). Уравнения (2.1) и (2.2) являются рекуррентными соотношениями, которые позволяют определить величину fN(t) в зависимости от fN -1(t + 1). Структура этих уравнений показывает, что при переходе от одной стадии процесса к следующей возраст оборудования увеличивается с t до (t + 1) лет, а число оставшихся стадий уменьшается с N до (N — 1). Расчет начинают с использования уравнения (2.1). Уравнения (2.1) и (2.2) позволяют оценить варианты замены и сохранения оборудования, с тем чтобы принять тот из них, который предполагает больший доход. Эти соотношения дают возможность не только выбрать линию поведения при решении вопроса о сохранении или замене оборудования, но и определить прибыль, получаемую при принятии каждого из этих решений. Пример 1. Определить оптимальный цикл замены оборудования при следующих исходных данных: Р = 10, S(t) = 0, f(t) = r(t) — u(t), представленных в табл. 2.1.
Таблица 2.1
Решение. Уравнения (2.1) и (2.2) запишем в следующем виде:
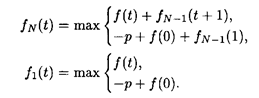
Для N = 1
Для N = 2
Вычисления продолжаем до тех пор, пока не будет выполнено условие f 1(1) > f 2(2), т.е. в данный момент оборудование необходимо заменить, так как величина прибыли, получаемая в результате замены оборудования, больше, чем в случае использования старого. Результаты расчетов помещаем в таблицу, момент замены отмечаем звездочкой, после чего дальнейшие вычисления по строчке прекращаем (табл. 2.2). Таблица 2.2
Можно не решать каждый раз уравнение (2.3), а вычисления проводить в таблице. Например, вычислим f 4 (t):
Дальнейшие расчеты для f 4 (t) прекращаем, так как f 4(4) = 23 < f 3(1) = 24. По результатам вычислений и по линии, разграничивающей области решений сохранения и замены оборудования, находим оптимальный цикл замены оборудования. Для данной задачи он составляет 4 года. Ответ. Для получения максимальной прибыли от использования оборудования в двенадцатиэтапном процессе оптимальный цикл состоит в замене оборудования через каждые 4 года.
Оптимальное распределение ресурсов
Пусть имеется некоторое количество ресурсов х, которое необходимо распределить между п различными предприятиями, объектами, работами и т.д. так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Введем обозначения: xi — количество ресурсов, выделенных i -му предприятию (i = gi(xi) — функция полезности, в данном случае это величина дохода от использования ресурса xi, полученного i- м предприятием; fk(x) — наибольший доход, который можно получить при использовании ресурсов х от первых k различных предприятий. Сформулированную задачу можно записать в математической форме:
при ограничениях:
Для решения задачи необходимо получить рекуррентное соотношение, связывающее fk(x) и fk- 1 (x). Обозначим через хk количество ресурса, используемого k- мспособом (0 ≤ xk ≤ х), тогда для (k — 1) способов остается величина ресурсов, равная (x — xk). Наибольший доход, который получается при использовании ресурса (x — xk) от первых (k — 1 ) способов, составит fk- 1 (x — xk). Для максимизации суммарного дохода от k- гo и первых (k — 1) способов необходимо выбрать xk таким образом, чтобы выполнялись соотношения
Рассмотрим конкретную задачу по распределению капиталовложений между предприятиями.
Распределение инвестиций для эффективного использования потенциала предприятия
Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме. Для расширения производства совет директоров выделяет средства в объеме 120 млн р. с дискретностью 20 млн р. Прирост выпуска продукции на предприятиях зависит от выделенной суммы, его значения представлены предприятиями и содержатся в табл. 2.3. Найти распределение средств между предприятиями, обеспечивающее максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить не более одной инвестиции.
Таблица 2.3
Решение. Разобьем решение задачи на четыре этапа по количеству предприятий, на которых предполагается осуществить инвестиции.
Рекуррентные соотношения будут иметь вид: для предприятия № 1
для всех остальных предприятий
Решение будем проводить согласно рекуррентным соотношениям в четыре этапа. 1-й этап. Инвестиции производим только первому предприятию. Тогда
2-й этап. Инвестиции выделяем первому и второму предприятиям. Рекуррентное соотношение для 2-го этапа имеет вид
Тогда при х = 20 f 2(20) = max (8 + 0,0 + 10) = max (8, 10) = 10, при x = 40 f 2(40) = max (16,8 + 10,20) = max (16, 18, 20) =20, при х = 60 f 2(60) = max (25,16 + 10, 8 + 20,28) = max (25,26, 28,28) =28, при х = 80 f 2(80) = max (36,25 + 10,16 + 20,8 + 28,40) = max (36, 35, 36, 36, 40) = 40, при х = 100 f 2(100) = max (44,36 + 10,25 + 20,16 + 28,8 + 40,48) = max (44, 46, 45, 44, 48, 48) = 48, при х = 120 f 2(120) = max (62,44 + 10,36 +20,25 + 28,16 + 40,8 + 48,62) = max (62, 54, 56, 53, 56, 56, 62) = 62. 3-й этап. Финансируем 2-й этап и третье предприятие. Расчеты проводим по формуле
Тогда при х = 20 f 3(20) = mах (10, 12) = 12, при x = 40 f 3(40) = max (20,10 + 12,21) = max (20, 22, 21) = 22, при х = 60 f 3(60) = max (28,20 + 12,10 + 21,27) = max (28, 32, 31, 27) = 32, при х = 80 f 3(80) = max (40,28 + 12,20 + 21,10 + 27,38) = max (40, 40, 41, 37, 38) = 41, при x = 100 f 3(100) = max (48,40 + 12,28 + 21,20 + 27,10 + 38,50) = max (48, 52, 49, 47, 48, 50) = 52, при х = 120 f 3(120) = max (62,48 + 12,40 + 21,28 + 27,20 + 38,10 + 50,63) = max (62, 60, 61, 55, 58, 60, 63) = 63. 4-й этап. Инвестиции в объеме 120 млн р. распределяем между 3-м этапом и четвертым предприятием. При х = 120 f 4(120) = max (63,52 + 11,41 + 23,32 + 30,22 + 37,12 + 51,63) = max (63, 63, 64, 62, 59, 63, 63) = 64. Получены условия управления от 1-го до 4-го этапа. Вернемся от 4-го к 1-му этапу. Максимальный прирост выпуска продукции в 64 млн р. получен на 4-м этапе как 41 + 23, т.е. 23 млн р. соответствуют выделению 40 млн р. четвертому предприятию (см. табл. 2.3). Согласно 3-му этапу 41 млн р. получен как 20 + 21, т.е. 21 млн р. соответствует выделеник 40 млн р. третьему предприятию. Согласно 2-этапу 20 млн р. получено при выделении 40 млн р. второму предприятию. Таким образом, инвестиции в объеме 120 млн р. целесообразно выделить второму, третьему и четвертому предприятиям по 40 млн р. каждому, при этом прирост продукции будет максимальным и составит 64 млн р.
Минимизация затрат на строительство и эксплуатацию предприятий
Задача по оптимальному размещению производственных предприятий может быть сведена к задаче распределения ресурсов согласно критерию минимизации с учетом условий целочисленности, накладываемых на переменные. Пусть задана потребность в пользующемся спросом продукте на определенной территории. Известны пункты, в которых можно построить предприятия, выпускающие данный продукт. Подсчитаны затраты на строительство и эксплуатацию таких предприятий.
Необходимо так разместить предприятия, чтобы затраты на их строительство и эксплуатацию были минимальные. Введем обозначения: х — количество распределяемого ресурса, которое можно использовать п различными способами, xi — количество ресурса, используемого по i -му способу (i = gi(xi) — функция расходов, равная, например, величине затрат на производство при использовании ресурса xi по i -му способу; φk(x) — наименьшие затраты, которые нужно произвести при использовании ресурса х первыми k способами. Необходимо минимизировать общую величину затрат при освоении ресурса x всеми способами:
при ограничениях
Экономический смысл переменных xi состоит в нахождении количества предприятий, рекомендуемого для строительства в i- м пункте. Для удобства расчетов будем считать, что планируется строительство предприятий одинаковой мощности. Рассмотрим конкретную задачу по размещению предприятий. Пример. В трех районах города предприниматель планирует построить пять предприятий одинаковой мощности по выпуску хлебобулочных изделий, пользующихся спросом. Необходимо разместить предприятия таким образом, чтобы обеспечить минимальные суммарные затраты на их строительство и эксплуатацию. Значения функции затрат gi (x) приведены в табл. 2.4.
Таблица 2.4
В данном примере gi(х) — функция расходов в млн р., характеризующая величину затрат на строительство и эксплуатацию в зависимости от количества размещаемых предприятий в i -м районе; φk (x) — наименьшая величина затрат в млн. р., которые нужно произвести при строительстве и эксплуатации предприятий в первых k районах. Решение. Решение задачи проводим с использованием рекуррентных соотношений: для первого района
для остальных районов
Задачу будем решать в три этапа. 1-й этап. Если все предприятия построить только в первом районе, то
минимально возможные затраты при х = 5 составляют 76 млн р. 2-й этап. Определим оптимальную стратегию при размещении предприятий только в первых двух районах по формуле
Найдем φ 2(l): g 2(1) + φ 1(0) = 10 + 0 = 10, g 2(0) + φ 1(l)= 0 +11 = 11, φ 2(l) = min (10, 11) = 10.
Вычислим φ 2(2): g 2(2) + φ 1(0) = 19 + 0 = 19, g 2(l) + φ 1(l) = 10 + 11 = 21, g 2(0) + φ 1 (2) = 0 + 18 = 18, φ 2(2) = min (19, 21, 18) = 18.
Найдем φ 2(3): g 2(3) + φ 1 (0) = 34 + 0 = 34, g 2(2) + φ 1(l) = 19 + 11 = 30, g 2(1) + φ 1(2) = 10 + 18 = 28, g 2(0) + φ 1(3) = 0 + 35 = 35, φ 2(3) = min (34, 30, 28, 35) = 28.
Определим φ 2(4):
g 2(4) + φ 1(0) = 53 + 0 = 53, g 2(3) + φ 1(l) = 34 + 11 = 45, g 2(2) + φ1 (2) = 19 + 18 = 37, g 2(l) + φ 1(3) = 10 + 35 = 45, g 2(0) + φ 1(4) = 0 + 51 = 51, φ 2(4) = min (53, 45, 37, 45, 51) = 37.
Вычислим φ 2(5): g 2(5) + φ 1(0) = 75 + 0 = 75, g 2(4) + φ 1(l) = 53 + 11 = 64, g 2(3) + φ 1(2) = 34 + 18 = 52, g 2(2) + φ 1(3) = 19 + 35 = 54, g 2(1) + φ 1(4) = 10 + 51 = 61, g 2(0) + φ 1(5) = 0 + 76 = 76, φ 2(5) = min (75, 64, 52, 54, 61, 76) = 52. 3-й этап. Определим оптимальную стратегию при размещении пяти предприятий в трех районах по формуле φ 3 (x) = min{ g 3(x 3) + φ 2(x – х 3)}. Найдем φ 3(5): g 3(5) + φ 2(0) = 74 + 0 = 74, g 3(4) + φ 2(1) = 54 + 10 = 64, g 3(3) + φ 2(2) = 36 + 18 = 54, g 3(2) + φ 2(3) = 20 + 28 = 48, g 3(1) + φ 2(4) = 9 + 37 = 46, g 3(0) + φ 2(5) = 0 + 52 = 52,
φ 3(5) = min (74, 64, 54, 48, 46, 52) = 46.
Минимально возможные затраты при х = 5 составляют 46 млн р. Определены затраты на строительство предприятий от 1-го до 3-го этапа. Вернемся 3-го к 1-му этапу. Минимальные затраты в 46 млн р. на 3-м этапе получены как 9 + 37, т.е. 9 млн р. соответствуют строительству одного предприятия в третьем районе (см. табл. 2.4). Согласно 2-му этапу 37 млн р. получены как 19 + 18, т.е. 19 млн р. соответствуют строительству двух предприятий во втором районе. Согласно 1-му этапу 18 млн р. соответствуют строительству двух предприятий в первом районе. Ответ. Оптимальная стратегия состоит в строительстве одного предприятия в третьем районе, по два предприятия во втором и первом районах, при этом минимальная стоимость строительства и эксплуатации составит 46 ден. ед.
Нахождение рациональных затрат при строительстве трубопроводов и транспортных артерий
Требуется проложить путь (трубопровод, шоссе) между двумя пунктами А и В таким образом, чтобы суммарные затраты на его сооружение были минимальные. Решение. Разделим расстояние между пунктами А и В на шаги (отрезки). На каждом шаге можем двигаться либо строго на восток (по оси X), либо строго на север (по оси Y). Тогда путь от А в В представляет ступенчатую ломаную линию, отрезки которой параллельны одной из координатных осей. Затраты на сооружение каждого из отрезков известны (рис. 2.2) в млн р.
Рис. 2.2 Разделим расстояние от А до В в восточном направлении на 4 части, в северном – на 3 части. Путь можно рассматривать как управляемую систему, перемещающуюся под влиянием управления из начального состояния А в конечное В. Состояние этой системы перед началом каждого шага будет характеризоваться двумя целочисленными координатами х и у. Для каждого из состояний системы (узловой точки) найдем условное оптимальное управление. Оно выбирается так, чтобы стоимость всех оставшихся шагов до конца процесса была минимальна. Процедуру условной оптимизации проводим в обратном направлении, т.е. от точки В к точке А. Найдем условную оптимизацию последнего шага (рис. 2.3).
Рис. 2.3 В точку В можно попасть из B 1 или В 2. В узлах запишем стоимость пути. Стрелкой покажем минимальный путь. Рассмотрим предпоследний шаг (рис. 2.4).
Рис. 2.4 Для точки В 3 условное управление — по оси X, а для точки B 5 — по оси Y. Управление для точки В 4 выбираем как
т.е. по оси Y. Условную оптимизацию проводим для всех остальных узловых точек (рис. 2.5).
Рис. 2.5 Получим
где с — север, в — восток. Минимальные затраты составляют
Если решать задачу исходя из оптимальности на каждом этапе, то решение будет следующим:
Затраты составят 10 +12 + 11 + 10 + 9 + 13 +10 = 75 > 71. Ответ. Прокладывать путь целесообразно по схеме: с, с, в, с, в, в, в, при этом затраты будут минимальные и составят 71 млн р. Глава 3. СЕТЕВЫЕ МОДЕЛИ
До появления сетевых методов планирование работ, проектов осуществлялось в небольшом объеме. Наиболее известным средством такого планирования был ленточный график Ганта, недостаток которого состоит в том, что он не позволяет установить зависимости между различными операциями. Современное сетевое планирование начинается с разбиения программы работ на операции. Определяются оценки продолжительности операций, и строится сетевая модель (график). Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала ее реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями графика. Календарный график выявляет критические операции, которым надо уделять особое внимание, чтобы закончить все работы в директивный срок. Что касается некритических операций, то календарный план позволяет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффективном применении как трудовых, так и финансовых ресурсов.
Основные понятия сетевой модели
Сетевая модель — графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа. Граф — схема, состоящая из заданных точек (вершин), соединенных системой линий. Отрезки, соединяющие вершины, называются ребрами (дугами) графа. Ориентированным называется такой граф, на котором стрелкой указаны направления всех его ребер (дуг), что позволяет определить, какая из двух его граничных вершин является начальной, а какая — конечной. Исследование таких сетей проводится методами теории графов. Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график — это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента — работа и событие. Работа — это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата. Фиктивная работа — это связь между результатами работ (событиями), не требующая затрат времени и ресурсов. Событие — это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ. Путь — это любая непрерывная последовательность (цепь) работ и событий. Критический путь — это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называют критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ. При построении сетевых моделей необходимо соблюдать следующие правила. 1. Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 3.1). 3. В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рис. 3.2).
4. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 3.3). 5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 3.4). Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычеркивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Пример нумерации сетевого графика показан на рис. 3.5.
Рис. 3.5 Продолжительность выполнения работ устанавливается на основании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором — стохастическими (вероятностными). Рассмотрим в качестве примера программу создания нового бытового прибора, пользующегося спросом у населения. Необходимые данные приведены в табл. 3.1. На основании данных таблицы построим сетевой график создания прибора с учетом вышеизложенных рекомендаций (рис. 3.6).
Рис. 3.6 Таблица 3.1
Расчет временных параметров сетевого графика
Основным временным параметром сетевого графика является продолжительность критического пути. Расчет критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного события и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события определяется одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления. Рассмотрим прямой проход:
ti р.н. — ранний срок начала всех операций, выходящих из события i. Если i = 0, то t 0р.н. = 0; tj р.н. — ранний срок начала всех операций, входящих в j. Тогда
где tij — продолжительность операции (i,j);
Прямой проход закончился, начинаем обратный: ti п.o — поздний срок окончания всех операций, входящих в событие i. Если i = п, где п — завершающее событие сети, то tn п.o = tn р.н. и является отправной точкой обратного прохода;
ti п.о =
Используя результаты вычислений при прямом и обратном проходах, можно определить операции критического пути. Операция (i, j) принадлежит критическому пути, если она удовлетворяет условиям:
Для рассматриваемого примера критический путь включает операции (0,2), (2,3), (3,4), (4,5), (5,6). Операции связаны еще с двумя сроками: tij п.н. — поздний срок начала работы. Он является наиболее поздним (максимальным) из допустимых моментов начала данной работы, при котором еще возможно выполнение всех последующих работ в установленный срок:
tij р.o — ранний срок окончания работы. Он является наиболее ранним (минимальным) из возможных моментов окончания работы при заданной продолжительности работ:
Различают два вида резервов времени: полный резерв (r п) и свободный резерв (r св). Полный резерв времени показывает, на сколько может быть увеличена сумма продолжительности всех работ относительно критического пути. Он представляет собой разность между максимальным отрезком времени, в течение которого может быть выполнена операция, и ее продолжительностью (tij) и определяется как
Свободный резерв времени — максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы при условии, что все события наступают в ранние сроки:
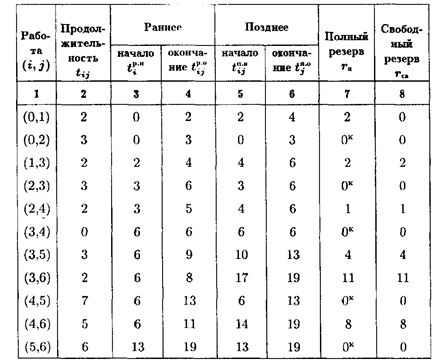
Результаты расчета критического пути и резервов времени некритических операций представлены в нижеследующей таблице. Следует отметить, что критические операции должны иметь нулевой полный резерв времени, при этом свободный резерв также должен быть равен нулю.
Построение сетевого графика и распределение ресурсов
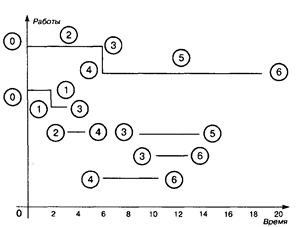
Конечным результатом выполняемых на сетевой модели расчетов является сетевой график (план). При построении сетевого графика необходимо учитывать наличие ресурсов, так как одновременное выполнение некоторых операций из-за ограничений, связанных с рабочей силой, оборудованием и другими видами ресурсов, иногда оказывается невозможным. Именно в этом отношении представляют ценность полные резервы времени некритических операций. Сдвигая некритическую операцию в том или ином направлении, но в пределах ее полного резерва времени, можно добиться снижения максимальной потребности в ресурсах. Оданако даже при отсутствии ограничений на ресурсы полные резервы времени обычно используются для выравнивания потребностей в ресурсах на протяжении всего срока реализации программы работ. Это означает, что работы удастся выполнить более или менее постоянным составом рабочей силы. Таблица 3.2
Рис. 3.7
На рис. 3.8 показана потребность в рабочей силе при условии выбора в качестве календарных сроков некритических операций начала их ранних сроков, на рис. 3.9 — потребность в рабочей силе при выборе наиболее поздних сроков. Пунктирной линией представлена потребность критических операций, которая должна быть удовлетворена, если нужно выполнить все работы в минимально возможный срок. Оптимальное решение задачи равномерного использования ресурсов (минимизация максимальной потребности в ресурсах) представлено на рис. 3.10, уточненный график выполнения работ указан на рис. 3.11.
Рис. 3.8 Рис. 3.9
Рис. 3.10 Рис. 3.11 Учет стоимостных факторов при реализации сетевого графика
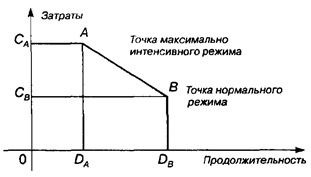
Стоимостные факторы при реализации сетевого графика учитываются путем определения зависимости "затраты-продолжительность" для каждой операции. При этом рассматриваются прямые затраты, а косвенные типа административных или управленческих расходов не принимаются во внимание. На рис. 3.12 показана линейная зависимость стоимости операции от ее продолжительности. Точка (DB, СB), где DB — продолжительность операции, а СB — ее стоимость, соответствует нормальному режиму выполнения операции. Продолжительность операции можно уменьшить (сжать), увеличив интенсивность использования ресурсов, а следовательно, увеличив стоимость операции. Однако существует предел, называемый минимальной продолжительностью операции. За точкой, соответствующей этому пределу (точка максимально интенсивного режима), дальнейшее увеличение интенсивности использования ресурсов ведет лишь к увеличению затрат без сокращения продолжительности операции. Этот предел обозначен на рис. 3.12 точкой А с координатами (DA,СA). Линейная зависимость "затраты-продолжительность" принимается из соображений удобства, так как ее можно определить для любой операции по двум точкам нормального и максимально интенсивного режимов, т.е. по точкам А и В. Использование нелинейной зависимости "затраты-продолжительность" существенно усложняет вычисления. Поэтому иногда нелинейную зависимость можно аппроксимировать кусочно-линейной (рис. 3.13), когда операция разбивается на части, каждая из которых соответствует одному линейному отрезку. Следует отметить, что наклоны этих отрезков при переходе от точки нормального режима к точке максимально интенсивного режима возрастают. Если это условие не выполняется, то аппроксимация не имеет смысла.
Рис. 3.12 Рис. 3.13
Определив зависимость "затраты-продолжительность", для всех операций сети принимают нормальную продолжительность. Далее рассчитывается сумма затрат на все операции сети при этой продолжительности работ. На следующем этапе рассматривается возможность сокращения продолжительности работ. Этого можно достичь за счет уменьшения продолжительности какой-либо критической операции, только критические операции и следует подвергать анализу. Чтобы добиться сокращения продолжительности выполнения работ при минимально возможных затратах, необходимо в максимально допустимой степени сжать ту критическую операцию, у которой наклон кривой "затраты-продолжительность" наименьший. В результате сжатия критической операции получают новый календарный график, возможно, с новым критическим путем. Стоимость работ при новом календарном графике будет выше стоимости работ по предшествующему графику. На следующем этапе этот новый график вновь подвергается сжатию за счет следующей критической операции с минимальным наклоном кривой "затраты-продолжительность" при условии, что продолжительность этой операции не достигла минимального значения. Подобная процедура повторяется, пока все критические операции не будут находиться в режиме максимальной интенсивности. Полученный таким образом оптимальный календарный график соответствует минимуму прямых затрат.
Обоснование привлекательности проекта по выпуску продукции
Для финансирования проектов по строительству и наладке изготовления конкурентоспособной продукции в большинстве случаев фирмам требуются инвестиции. Включение в проект материалов с оптимизацией сетевых моделей в части обоснования сроков возврата инвестиций делает проект более привлекательным и способствует принятию инвестором положительного решения. Пример 1. Предприятие решило для улучшения финансового состояния наладить выпуск конкурентоспособной продукции (мороженого). Для переоборудования цеха (участка) под выпуск этой продукции необходимо выполнить: 1) подготовку технического задания на переоборудование участка (30 дн.); 2) заказ и поставку нового
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 645; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.49.19 (0.021 с.) |







 );
);




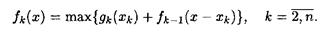



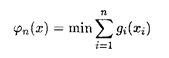













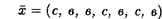







 (tj п.о - ti,j) для всех операций (i,j);
(tj п.о - ti,j) для всех операций (i,j);