Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель 1 (системы с ожиданием)Содержание книги
Поиск на нашем сайте
На СМО, состоящую из n приборов, поступает пуассоновский поток требований на обслуживание интенсивностью a. Время обслуживания каждого требования случайное с экспоненциальной функцией распределения и интенсивностью обслуживания b. Если требование, поступившее в систему, застает все приборы занятыми, то оно встает в очередь и ждет до тех пор, пока прибор не освободится. В каждый момент времени любой прибор может обслуживать не более одного требования. Требуется проанализировать СМО. Обозначим через В соответствие с моделью имеем размеченный граф состояний СМО:
Рис. 4.5 Замечание. Для данной модели необходимо выполнение следующего условия:
то есть, входящий поток меньше, чем суммарный выходящий, иначе система не будет функционировать. Определим показатели эффективности функционирования СМО: 1)
2)
3) Õ - вероятность того, что все приборы заняты (
4)
5)
6) вероятность того, что время ожидания в очереди больше среднего
7) A – средняя длина очереди:
8) B - среднее число требований, находящихся в системе:
9) À 0 – среднее число свободных приборов
10) À з - среднее число приборов, занятых обслуживанием:
11) R – среднее число обслуживаемых требований:
12)
13)
14)
Пример 1. Станция «Железная дорога» в мегаполисе принимает составы для разгрузки угля на
Решение. Условие существования решения 1). Вероятность того, что станция свободна 2). Вероятность того, что все платформы заняты 3). Время ожидания разгрузки для каждого состава в среднем составляет 4). Вероятность того, что время ожидания в очереди больше среднего 5). Средняя длина очереди 6). Среднее число занятых платформ 7). Среднее число составов на станции 8). Среднее время нахождение состава на станции 9). Коэффициент загрузки станции 10). Коэффициент простоя В среднем каждая платформа простаивает 20% времени. Для изменения времени простоев будем варьировать число платформ
Таблица 4.1
Из табл. 4.1 следует, что при числе платформ Дальнейшее увеличение числа платформ хотя и улучшает показатели, но для окончательного ответа проведем экономические расчеты. Определим суммарные потери за сутки. За лучший (суб-оптимальный) вариант примем тот, для которого издержки наименьшие. Имеем из (3.46) Результаты расчетов приведены в табл. 4.2.
Таблица 4.2
Из таблицы следует, что наиболее экономичным оказался вариант с Замечание. При применении экономического показателя важно правильно оценить реальные издержки, которые могут изменяться, например, от времени года, от объема запасов угля и пр. Приведенные исходные данные демонстрируют скорее метод анализа, чем претензии на соответствие реально существующим издержкам.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 657; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.006 с.) |

 - вероятность того, что в СМО находится k требований (состояние
- вероятность того, что в СМО находится k требований (состояние  ),
),  .
.

 - вероятность того, что все приборы свободны:
- вероятность того, что все приборы свободны: ;
;
 ):
): ;
; - вероятность того, что все приборы заняты обслуживанием и s требований в очереди:
- вероятность того, что все приборы заняты обслуживанием и s требований в очереди: ,
,  ;
; - среднее время, в течение которого требование ждет начала обслуживания:
- среднее время, в течение которого требование ждет начала обслуживания: ;
; ;
; ;
; ;
; ;
; ;
; ;
; - коэффициент простоя приборов:
- коэффициент простоя приборов: ;
; - коэффициент загрузки приборов:
- коэффициент загрузки приборов: ;
; - суммарные потери за отчетный период T:
- суммарные потери за отчетный период T: ,
, - стоимость потерь, связанных с простаиванием требований в очереди, в единицу времени;
- стоимость потерь, связанных с простаиванием требований в очереди, в единицу времени; - стоимость потерь за простой обслуживающего устройства в единицу времени;
- стоимость потерь за простой обслуживающего устройства в единицу времени; - стоимость эксплуатации прибора при обслуживании требований в единицу времени.
- стоимость эксплуатации прибора при обслуживании требований в единицу времени. платформах. В среднем за сутки на станцию прибывают 16 составов с углем. Поступление носит случайный характер. Плотность прихода составов показала, что поступление на разгрузку удовлетворяет пуассоновскому потоку с параметром
платформах. В среднем за сутки на станцию прибывают 16 составов с углем. Поступление носит случайный характер. Плотность прихода составов показала, что поступление на разгрузку удовлетворяет пуассоновскому потоку с параметром 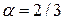 состава в час. Время разгрузки состава является случайной величиной, удовлетворяющей экспоненциальному закону со средним временем разгрузки
состава в час. Время разгрузки состава является случайной величиной, удовлетворяющей экспоненциальному закону со средним временем разгрузки 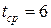 час. Простой состава в сутки составляет
час. Простой состава в сутки составляет  y.e; простой платформы в сутки за опоздание прихода состава -
y.e; простой платформы в сутки за опоздание прихода состава - 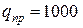 y.e; стоимость эксплуатации платформы в сутки -
y.e; стоимость эксплуатации платформы в сутки -  y.e. Издержки подсчитать за сутки. Требуется провести анализ эффективности функционирования станции.
y.e. Издержки подсчитать за сутки. Требуется провести анализ эффективности функционирования станции. выполнено. Имеем
выполнено. Имеем  1/сутки,
1/сутки, 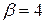 1/сутки. В соответствие с моделью показателями эффективности являются:
1/сутки. В соответствие с моделью показателями эффективности являются: . Это означает, что в течение суток станция свободна»19 мин.
. Это означает, что в течение суток станция свободна»19 мин. . То есть, около 13 ч 20 мин. все платформы заняты.
. То есть, около 13 ч 20 мин. все платформы заняты. ч.
ч. , то есть, каждый третий состав ожидает больше 3-х часов.
, то есть, каждый третий состав ожидает больше 3-х часов.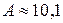 . Очередь велика. Подъездные пути необходимо дублировать.
. Очередь велика. Подъездные пути необходимо дублировать. .
. .
. .
. .
.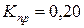 .
. . Результаты расчетов сведем в табл. 4.1.
. Результаты расчетов сведем в табл. 4.1. , ч
, ч
 почти в 4 раза снижается время ожидания разгрузки, а число составов, ожидающих разгрузки
почти в 4 раза снижается время ожидания разгрузки, а число составов, ожидающих разгрузки  , то есть, почти в 6 раз.
, то есть, почти в 6 раз. .
.