
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест №1. Имитационная модель системы массового обслуживанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тесты для магистрантов по дисциплинам цикла Математическое моделирование Перечень тестов: Тест №1. Имитационная модель системы массового обслуживания Тест№2. Классическая система массового обслуживания с очередями Тест № 3 – Классическая система массового обслуживания отказами. Тест№4. Теория расписаний. Задача упорядочения. Тест№5. Теория расписаний. Задача распределения. Тест№6. Моделирование оптимального управления порожними вагонами различных форм собственности. Тест № 7 – Сети Петри. Тест № 8 – Оптимизация распила входного материала при изготовлении металлопластиковых окон. Тест №1. Имитационная модель системы массового обслуживания В соответствии с блок-схемой алгоритма имитационного моделирования системы массового обслуживания с отказами, приведенной ниже,
составить программу функционирования модели СМО с отказами. Для всех вариантов: число опытов N (число рабочих дней, например) взять равным N = 200, продолжительность опыта Tкон (продолжительность рабочего дня) взять равным Tкон = 8 часов = 480 минут, число линий обслуживания (число занятых обслуживанием устройств) «n» взять равным n = 5. В соответствии с номером варианта и данными таблицы, запрограммировать моделирование случайных величин Таблица
Запрограммировать накопление числа выполненных заявок и числа отказов в соответствующих счетчиках. После «проигрывания» модели 200 раз запрограммировать вычисление и вывод на печать (на экран) следующих характеристик СМО с отказами: - среднее число выполненных заявок и оценку вероятности выполнения заявки; - среднее число отказов и оценку вероятности отказа. Аналогично предыдущему разработать модель СМО с очередью с теми же исходными данными, что и в предыдущем разделе и с помощью этой модели получить следующие характеристики: - среднюю длину очереди; - оценку вероятности отсутствия очереди; - оценку вероятности того, что все устройства обслуживания будут заняты.
При определенных условиях, накладываемых на систему массового обслуживания с отказами (стационарность, ординарность и отсутствие последействия для потока заявок и для времени выполнения заявок и т. д.) для характеристик системы могут быть получены аналитические выражения. Будем называть такие системы классическими. Вероятность k – того состояния системы pk вычисляется по формуле pk = где Вероятность отказа pотк = pn, то - есть она вычисляется по формуле (1) при k = n. Среднее число занятых устройств m вычисляется по формуле m = Задание: зная параметры системы массового обслуживания (СМО) с отказами:
Найти ответ на вопрос: сколько должно быть устройств обслуживания, чтобы вероятность отказа была не более 0,1?
Задание Построить оптимальное по быстродействию расписание выполнения совокупности работ A=(a1, a2, a3, a4, a5) на ресурсах A, B, C. Времена выполнения каждой работы на каждом ресурсе приведены в таблице для каждого варианта.
Задания В таблицах по каждому варианту представлены: запасы вагонов в пунктах Ai – в последнем столбике таблицы (в правом верхнем углу клетки-вагоны перевозчика, в левом нижнем углу клетки-вагоны других форм собственности), заявки на вагоны от пунктов Bj – в последней строке таблицы, в правом верхнем углу остальных клеток транспортные расходы по перемещению одного вагона из Ai в Bj - Cij для вагонов перевозчика, а в левом нижнем углу - Cij* для вагонов других форм собственности. Составить оптимальный план распределения вагонов. №1
№2
№3
№4
№5
№6
№7
№8
№9
№10
№11
№12
№13
№14
№15
№16
№17
№18
|


 k
k
 (интервал между заявками) и tзан (время выполнения заявок) по их плотностям вероятности f1(
(интервал между заявками) и tзан (время выполнения заявок) по их плотностям вероятности f1( ) и f2(t) из таблицы.
) и f2(t) из таблицы. )
)
 0
0 


 0
0 

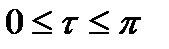
 e -
e -  /2,
/2, 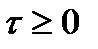

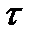 3,
3, 
 , 0
, 0 
 , 0
, 0 
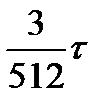 2, 0
2, 0 

 2,
2,  , 0
, 0 


 2 ,
2 , 
 e-x/3,
e-x/3, 

 0
0  k
k  / k! (1)
/ k! (1) ,
,  =
=  -1, k = 0, 1, 2, …, n (2)
-1, k = 0, 1, 2, …, n (2) (1 - pn) (3)
(1 - pn) (3) - интенсивность потока заявок,
- интенсивность потока заявок,  - интенсивность обслуживания, n – число каналов обслуживания, найти характеристики СМО: вероятности состояний p0, p1, p2, … pn; среднее число занятых устройств и вероятность отказа (в стационарном режиме). Значения параметров СМО для различных вариантов задания приведены в таблице:
- интенсивность обслуживания, n – число каналов обслуживания, найти характеристики СМО: вероятности состояний p0, p1, p2, … pn; среднее число занятых устройств и вероятность отказа (в стационарном режиме). Значения параметров СМО для различных вариантов задания приведены в таблице: k
k
 1
1
 Ak
Ak



