
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Cистемы массового обслуживания.Содержание книги
Поиск на нашем сайте Теория массового обслуживания – область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно, например, на предприятиях бытового обслуживания; в системах приема, переработки и передачи информации; автоматических линиях производства и др. На первичное развитие теории массового обслуживания оказали особое влияние работы датского ученого А.К. Эрланга (1878-1929). (Решение задачи обслуживания звонков, поступающих на телефонную станцию.) Система массового обслуживания считается заданной, если известны: 1) поток требований, его характер; 2) множество обслуживающих приборов; 3) дисциплина обслуживания (совокупность правил, задающих процесс обслуживания). Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (или прихода новой заявки, или окончания обслуживания, или момента, когда заявка, которой надоело ждать, покидает очередь). Классификация СМО
Рис.1: Классификация систем массового обслуживания. . К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на подналадку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно. Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и др. Для этих систем поступающий поток требований можно считать неограниченным. Под дисциплиной подключения каналов к обслуживанию понимают правила, по которым обслуживающие приборы подключаются к обслуживанию поступающих заявок, при этом все заявки считаются равноценными, с этой точки зрения различают две разновидности СМО: системы со взаимопомощью между каналами обслуживания и системы без взаимопомощи. Встречаются СМО, в которых для ускорения процесса обслуживания допускается подключение нескольких каналов к работе над одной заявкой. Например, два или несколько рабочих могут одновременно ремонтировать один станок или автомашину, по одному самолету может стрелять несколько зенитных орудий, вычисления для одной задачи могут быть, распараллелены между несколькими ЭВМ Многофазными называются СМО, которые состоят из нескольких последовательно соединенных отдельных подсистем массового обслуживания, причем входящий поток каждой последующей подсистемы является выходящим потоком предыдущей. Характеристики СМО. 1. Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступления требований иопределяется следующим соотношением: 2. Интенсивность обслуживания среднее число требований, обслуженных системой за единицу времени 3. Коэффициент загрузки: 4. Вероятность того, что поступающее в систему требование откажется присоединяться к очереди и теряется, Ротк. Этот показатель для системы массового обслуживания с отказами равен вероятности того, что в системе находится столько требований, сколько она содержит каналов обслуживания: Ротк = Pm, где т — число каналов обслуживания. Для системы с ограниченной длиной очереди Ротк равно вероятности того, что в системе находится т +l требований: Ротк = Pm+l, где l — допустимая длина очереди. Противоположным показателем является вероятность обслуживания требования Робсл = 1- Pотк. 5. Среднее количество требований, ожидающих начала обслуживания (средняя длина очереди): 6. Относительная (q) и абсолютная (А) пропускные способности системы. Эти величины находят соответственно по формулам: q = 1 - Ротк, A = λ. 7. Среднее число занятых обслуживанием приборов mз. Для системы массового обслуживания с отказами mз можно найти по формуле 8. Общее количество требований, находящихся в системе (М). Эту величину определяют следующим образом. Для систем массового обслуживания с отказами М = mз. Для систем массового обслуживания с ограниченной длиной очереди и ожиданием М = mз + Мож. 9. Среднее время ожидания требованиям начала обслуживания (Тож). Если известна функция распределения вероятности времени ожидания требованиям начала обслуживания Показатели, характеризующие экономические особенности, формируют обычно в соответствии с конкретным видом системы и ее назначением. Одним из общих экономических показателей является экономическая эффективность
где с — средний экономический эффект, полученный при обслуживании одного требования, t — рассматриваемый интервал времени, G п — величина потерь в системе. Для системы с отказами
Входящий поток требований. Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Поток событий называется регулярным, если события следуют одно за другим через одинаковые, строго фиксированные промежутки времени. Для многих реальных процессов поток требований достаточно хорошо описывается законом распределения Пуассона, согласно которому вероятность
Где λ — среднее число требований, поступивших на обслуживание в единицу времени. Такой поток является простейшим. Простейший поток обладает такими важными свойствами: 1. Свойство стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку, в среднем в сутки должно быть одинаковым для различных периодов времени, к примеру, в начале и в конце декады. 2. Отсутствие последействия, которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени. Например, число автомобилей, прибывших за материалами в десятый день месяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца. 3. Свойство ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю). На практике условия простейшего потока не всегда строго выполняются. Часто имеет место нестационарность процесса (в различные часы дня и различные дни месяца поток требований может меняться, он может быть интенсивнее утром или в последние дни месяца). Существует также наличие последействия, когда количество требований на отпуск товаров в конце месяца зависит от их удовлетворения в начале месяца. Наблюдается и явление неоднородности, когда несколько клиентов одновременно пребывают на склад за материалами. Однако в целом пуассоновский закон распределения с достаточно высоким приближением отражает многие процессы массового обслуживания. Почему такое предположение в ряде важных случаев оказывается верным, дает ответ теорема А.Я.Хинчина. Эта теорема имеет место в случае, когда входящий поток можно представить в виде суммы большого числа независимых потоков, ни один из которых не является сравнимым по интенсивности со всем суммарным потоком. Приведем “не строгую” формулировку этой теоремы. Теорема (А.Я.Хинчин) Если входящий поток представляет собой сумму большого числа независимых между собой стационарных и ординарных потоков, каждый из которых вносит малый вклад в общую сумму, то при одном дополнительном условии аналитического характера (которое обычно выполняется на практике) поток близок к простейшему. Применение этой теоремы на практике можно продемонстрировать, на следующем примере: поток судов дальнего плавания в данный грузовой порт, связанный со многими портами мира, можно считать близким к простейшему. Это дает нам право считать поток прибытия судов в порт распределенным согласно процесса Пуассона. Кроме того, наличие пуассоновского потока требований можно определить статистической обработкой данных о поступлении требований на обслуживание. Известно, что для него распределение промежутков времени между соседними событиями подчиняется экспоненциальному закону:
Интегрируя по частям, получим:
Потоки Пальма или потоки с ограниченным последействием являются обобщением потоков элементарных событий. Потоком Пальма называется поток, в котором промежутки времени между двумя соседними событиями представляют собой независимые случайные величины, распределенные по одному и тому же закону. Частным случаем потоков Пальма являются простейшие потоки, в которых интервалы между соседними событиями распределены по показательному закону. Если интервалы между событиями подчиняются гауссовскому распределению, то такие потоки называются нормальными. Очевидно, что для регулярного потока закон распределения выражается d -функцией. В теории массового обслуживания широко используются потоки Эрланга. Они образуются из простейших потоков путем применения к ним операции "просеивания". Эта операция заключается в том, что из простейшего потока удаляется некоторое число точек по определенному правилу. Если удаляются точки через одну, т.е. остается каждая 2-я точка, то поток Эрланга называется потоком 2-го порядка (Э2). Если удаляются две точки подряд и остается каждая 3-я точка, то получается поток Эрланга 3-го порядка (Э3). Если удаляются (k -l) точек подряд, а остается каждая k -я точка, то поток Эрланга называется потоком k -го порядка (Э k). Очевидно, что простейший поток является потоком Эрланга 1-го порядка. Можно показать, что функция распределение промежутков времени между соседними событиями имеет вид
Это так называемый закон Эрланга. При k =1 он вырождается в показательное распределение. Каждый интервал в потоке Э k равен: Т = STi, где Ti - независимые случайные величины, распределенные по показательному закону с первыми двумя моментами, определяемыми выражениями (7.1). Применяя теоремы о сложении математических ожиданий и дисперсий для суммы независимых случайных величин, получим
Время обслуживания. Время обслуживания одного требования τ — случайная величина, которая может изменятся в большом диапазоне. Она зависит как от стабильности работы обслуживающих устройств, так и от различных параметров, поступающих в систему, требований (к примеру, различной грузоподъемности транспортных средств, поступающих под погрузку или выгрузку). Случайная величина τ полностью характеризуется законом распределения, который определяется на основе статистических испытаний. На практике чаще всего принимают гипотезу о показательном законе распределения времени обслуживания. Он имеет место тогда, когда плотность распределения резко убывает с возрастанием времени t. Например, когда основная масса требований обслуживается быстро, а продолжительное обслуживание встречается редко. Наличие показательного закона распределения времени обслуживания устанавливается на основе статистических наблюдений. При показательном законе распределения времени обслуживания вероятность Fτ того, что время обслуживания продлиться не более чем t, равна:
где μ — интенсивность обслуживания одного требования одним обслуживающим устройством. Следует заметить, что если закон распределения времени обслуживания показательный, то при наличии нескольких обслуживающих устройств одинаковой мощности закон распределения времени обслуживания несколькими устройствами будет также показательным:
где m — количество обслуживающих устройств. При показательном распределении длительности обслуживания распределение длительности оставшейся части работы по обслуживанию не зависит от того, сколько оно уже продолжалось. Действительно, пусть
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |


 , где Т — среднее значение интервала между поступлением очередных требований.
, где Т — среднее значение интервала между поступлением очередных требований. , tобс — среднее время обслуживания.
, tобс — среднее время обслуживания.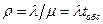 .
. , где Pn — вероятность того, что в системе находятся п требований.
, где Pn — вероятность того, что в системе находятся п требований.
 , то среднее время ожидания находится как математическое ожидание случайной величины Тож:
, то среднее время ожидания находится как математическое ожидание случайной величины Тож:  .
.
 , где qэ — стоимость эксплуатации одного прибора в единицу времени, qy — стоимость убытков в результате ухода требований из системы в единицу времени, qпр — стоимость единицы времени простоя прибора системы, тсв = т – т3. Для систем с ожиданием
, где qэ — стоимость эксплуатации одного прибора в единицу времени, qy — стоимость убытков в результате ухода требований из системы в единицу времени, qпр — стоимость единицы времени простоя прибора системы, тсв = т – т3. Для систем с ожиданием  , qож — стоимость потерь, связанных с простоем требований в очереди в единицу времени.
, qож — стоимость потерь, связанных с простоем требований в очереди в единицу времени. того, что в обслуживающую систему за промежуток время Δ t поступит именно k требований, равна
того, что в обслуживающую систему за промежуток время Δ t поступит именно k требований, равна .
. , для которого математическое ожидание и корень из дисперсии равны
, для которого математическое ожидание и корень из дисперсии равны ,
,  .
. . (7.1)
. (7.1) .
.



 означает вероятность того, что обслуживание, которое уже продолжается время а, продлится еще не менее чем t. Если длительность обслуживания распределена показательно, то
означает вероятность того, что обслуживание, которое уже продолжается время а, продлится еще не менее чем t. Если длительность обслуживания распределена показательно, то  ,
, 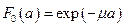 и
и  . Tак как
. Tак как  , то
, то  и, следовательно,
и, следовательно,  . Требуемое доказано.
. Требуемое доказано.


