Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограниченность дерева достижимости.Содержание книги
Поиск на нашем сайте
Дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, а также для определения возможной последовательности запусков. Решение этих задач ограничено существованием символа Матричные уравнения. Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Представим сеть Петри в виде двух матриц
Пусть e [ j ] — m -вектор, содержащий нули везде, за исключением j -й компоненты. Переход tj представляется m -вектором e [ j ] (строка), а маркировка m — n -вектором (столбец). Теперь переход tj в маркировке m разрешен, если m
где D = Для последовательности запусков переходов
Вектор Сохранение. Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть w — n - вектор-столбец. Тогда, если m — начальная маркировка, а m ' — произвольная достижимая маркировка, необходимо, чтобы m • w = m ' • w. Теперь, поскольку m ' достижима, существует последовательность запусков переходов
Следовательно, m • w = m ' • w = (m + Достижимость. Предположим, что маркировка m ' достижима из маркировки m. Тогда существует последовательность (возможно, пустая) запусков переходов
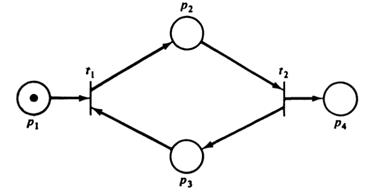
Пример. Рассмотрим маркированную сеть Петри на рис. 5.1. Матрицы
Рис 5.1: Примерсети Петри (решение задачи достижимости).
Для определения того, является ли маркировка (1, 8, 0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение
которое имеет решение х = (0, 4, 5). Это соответствует, например, последовательности Матричный подход к анализу сетей Петри очень перспективен, но имеет и некоторые трудности. Заметим прежде всего, что матрица D сама по себе не полностью отражает структуру сети Петри. Переходы, имеющие как входы, так и выходы из одной позиции (петли), представляются соответствующими элементами матриц Другая проблема — это отсутствие информации о последовательности запусков. Еще одна трудность заключается в том, что наличие целочисленного решения уравнения (5.6) является необходимым для достижимости, но недостаточным. Рассмотрим простую сеть Петри, приведенную на рис. 5.2. Если мы хотим определить, является ли маркировка (0, 0, 0, 1) достижимой из маркировки (1, 0, 0, 0), необходимо решить уравнение
Это уравнение имеет решение (1, 1), соответствующее двум последовательностям:
Рис 5.2: Сеть Петри, показывающая, что решение матричного уравнения — Необходимое, но недостаточное условие для решения задачи достижимости.
ЯЗЫКИ СЕТЕЙ ПЕТРИ. Лекция 6. Сети Петри для моделирования.
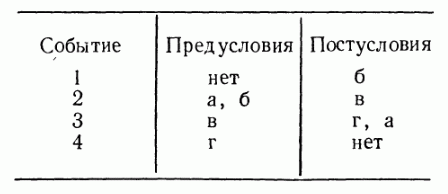
События и условия. Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. События — это действия, имеющие место в системе. Возникновением событий управляет состояние системы Состояние системы может быть описано множеством условий. Условие может принимать либо значение «истина», либо значение «ложь». Для того чтобы событие произошло, необходимо выполнение соответствующих условий. Эти условия называются предусловиями события. Возникновение события может вызвать нарушение предусловий и может привести к выполнению других условий, постусловий. В качестве примера рассмотрим задачу моделирования простого автомата-продавца. Автомат-продавец находится в состоянии ожидания до тех пор, пока не появится заказ, который он выполняет и посылает на доставку. Условиями для такой системы являются: а) автомат-продавец ждет; б) заказ прибыл и ждет; в) автомат-продавец выполняет заказ; г) заказ выполнен. Событиями будут: 1. Заказ поступил. 2. Автомат-продавец начинает выполнение заказа. 3 Автомат-продавец заканчивает выполнение заказа. 4. Заказ посылается на доставку. Таблица предусловий и постусловий:
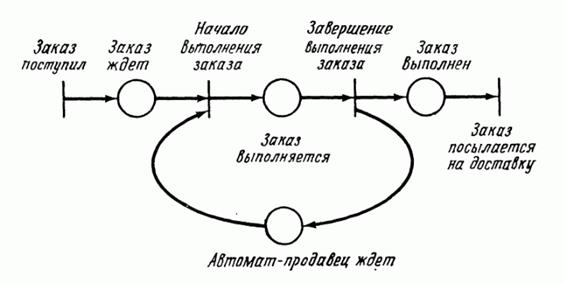
В сети Петри условия моделируются позициями, события — переходами. При этом входы перехода являются предусловиями соответствующего события; выходы — постусловиями. Возникновение события равносильно запуску соответствующего перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие фишки, представляющие выполнение предусловий и образует новые фишки, которые представляют выполнение постусловий. Сеть Петри на рис.6.1 иллюстрирует модель приведенного выше автомата-продавца.
Рис 6.1: Сеть Петри для простого автомата-продавца.
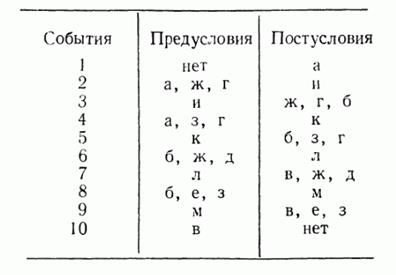
Более сложная система. Система автоавтомат-продавец состоит из трех различных автоматов M1, М2 и М3 и двух операторов F1 и F2. Оператор F1 воздействует на автоматы М1 и М2, а оператор F2 — на М1 и М3. Заказы требуют двух стадий обработки. Сначала они должны быть обработаны автоматом М1, затем либо автоматом М2 либо М3. Эта система будет иметь следующие условия: а) заказ прибыл и ждет обработки автоматом М1. б) заказ обработан автоматом М1 и ждет обработки либо автоматом М2, либо М3; в) заказ выполнен; г) автомат M1 незанят; д) автомат М2 незанят; е) автомат М3 незанят; ж) оператор F1 незанят; з) оператор F2 незанят; и) автомат М1 находится под воздействием оператора F1; к) автомат М1 находится под воздействием оператора F2, л) автомат М2 находится под воздействием оператора F1, м) автомат М3 находится под воздействием оператора F2. При этом могут происходить следующие события: 1. Поступление заказа. 2. Оператор F1 начинает выполнение заказа на автомате M1 3. Оператор F1 закончил выполнение заказа на автомате М1. 4. Оператор F2 начинает выполнение заказа на автомате М1. 5. Оператор F2 закончил выполнение заказа на автомате М1. 6. Оператор F1 начинает выполнение заказа на М2. 7. Оператор F1 закончил выполнение заказа на М2. 8. Оператор F2 начинает выполнение заказа на М3. 9. Оператор F2 закончил выполнение заказа на М3. 10. Заказ посылается на доставку. Таблица предусловий и постусловий:
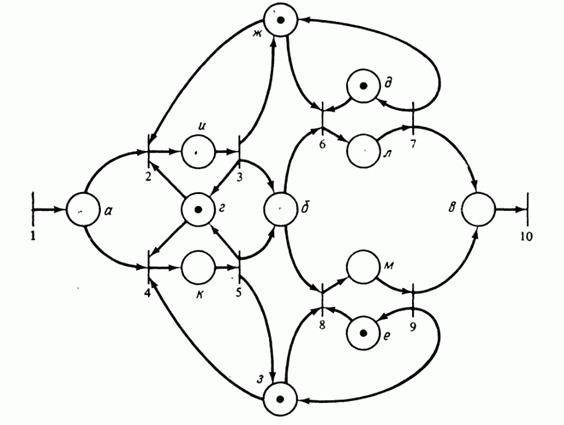
Рис 6.2: Сеть Петри для сложного автомата-продавца.
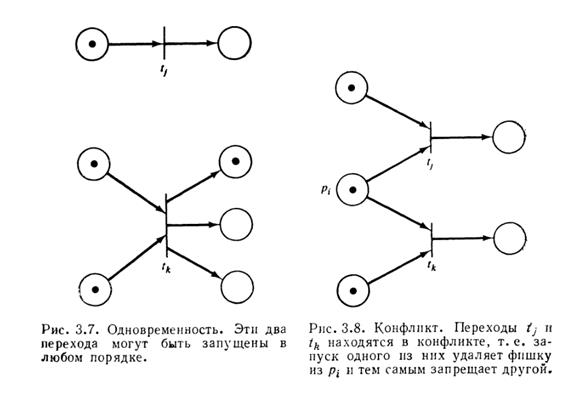
Одновременность и конфликт. В сети Петри два разрешенных невзаимодействующих события могут происходить независимо друг от друга. Сети Петри представляются идеальными для моделирования систем с распределенным управлением, в которых несколько процессов выполняются одновременно. В сети Петри отсутствует измерение времени или течение времени. Выполнение сети Петри (или поведение моделируемой системы) рассматривается как последовательность дискретных событий. Порядок появления событий является одним из возможных, допускаемых основной структурой. Это приводит к явной недетерминированности в выполнении сети Петри. Если в какой-то момент времени разрешено более одного перехода, то любой из нескольких возможных переходов может стать «следующим» запускаемым. Выбор запускаемого перехода осуществляется недетерминированным образом, т. е. случайно. Эта особенность сети Петри отражает тот факт, что в реальной жизненной ситуации, где несколько действий происходит одновременно, возникающий порядок появления событий — не однозначен; может возникнуть любая из множества последовательностей событий. Однако частичный порядок появления события — единственен. Для простоты обычно вводят следующее ограничение. Запуск перехода (и соответствующего события) рассматривается как мгновенное событие, занимающее нулевое время, и возникновение двух событий одновременно невозможно. Моделируемое таким образом событие называется примитивным; примитивные события мгновенны и неодновременны.
Рис 6.3: Понятие одновременности и конфликта в Сетях Петри.
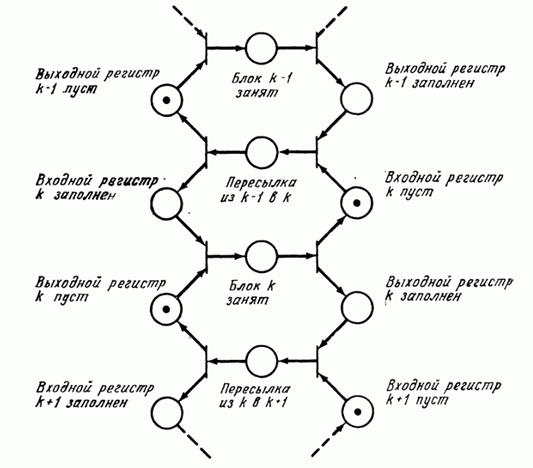
Аппаратное обеспечение ЭВМ. ЭВМ с конвейерной обработкой. Конвейер состоит из набора операций, которые могут выполняться одновременно. Когда операция k завершается, она передает свой результат операции (k + 1) и ожидает от операции (k — 1) нового задания. Для управления блоком k асинхронного конвейера необходимо знать, когда выполняются следующие условия: • входной регистр заполнен; • входной регистр пуст; • выходной регистр заполнен; • выходной регистр пуст; • блок занят; • блок свободен; • пересылка осуществлена.
Рис 6.4: Модель сети Петри устройства управления асинхронной ЭВМ с конвейерной обработкой.
Кратные функциональные блоки. Каждому функциональному блоку и каждому регистру поставим в соответствие позицию: если блок или регистр свободен — в позицию будет помещена фишка, если нет — фишки в позиции не будет. Кратные идентичные функциональные блоки показываются соответствующим числом фишек в позициях. На рис. 6.5 изображена часть сети Петри, которая может быть использована для моделирования выполнения инструкции, использующей блок u и регистры i, j и k.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.101.75 (0.01 с.) |

 . Символ
. Символ 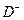 и
и 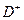 , представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим
, представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим (5.2)
(5.2) e [ j ] •
e [ j ] • 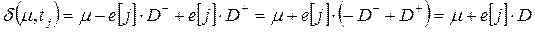 . (5.3)
. (5.3)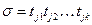 имеем
имеем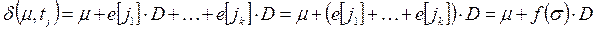 . (5.4)
. (5.4)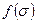 называется вектором запусков последовательности
называется вектором запусков последовательности 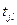 в последовательности
в последовательности 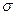 , которая переводит сеть из m в m '. Поэтому
, которая переводит сеть из m в m '. Поэтому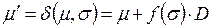 . (5.5)
. (5.5)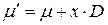 . (5.6)
. (5.6)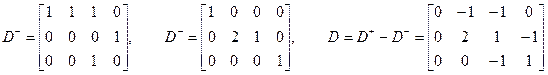 . (5.7)
. (5.7)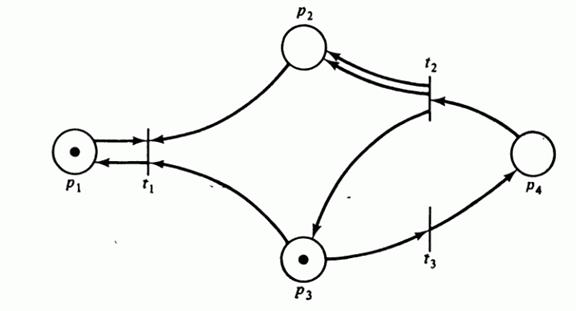
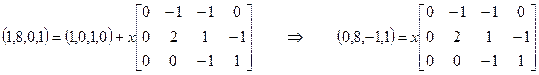 . (5.8)
. (5.8)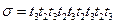 . (В принципе, может быть и другая последовательность.)
. (В принципе, может быть и другая последовательность.)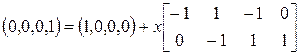 . (5.9)
. (5.9)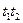 и
и 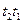 . Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни
. Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни 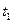 ни
ни 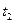 не разрешены.
не разрешены.