
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест№6. Моделирование оптимального управления порожними вагонами различных форм собственности.Содержание книги
Поиск на нашем сайте
Справочный материал Пусть в пунктах A1,A2,...,Am находятся порожние вагоны, причем в пункте Ai находится, соответственно, ai вагонов перевозчика и a*i вагонов других форм собственности (фирм, иностранных и т. д.). Эти вагоны должны быть поданы под погрузку в пункты B1,B2,..., Bn, причем заявки этих пунктов составляют, соответственно, b1,b2,..., bn вагонов. В общем случае исходными данными являются: m – число пунктов отправления (ПО); n – число пунктов назначения (ПН); C ij – транспортные расходы по перемещению одного вагона из пункта i в пункт j, " ij; при этом для вагонов других форм собственности эти расходы Cij* - это и собственно транспортные расходы и арендная плата и другие финансовые выплаты, которые перевозчик платит владельцам вагонов. Критерием задачи являются суммарные затраты на перемещение вагонов. Элементы модели:
C и С*– матрицы транспортных затрат; a=(a1, a2,..., am), a* =( a1*,a2*,..., am*) – вектора возможностей ПО; b=(b1, b2,..., bn) – вектор потребностей ПН. Удобно задачу представить в табличном виде:
Задача, отображающая таблицу, не является классической транспортной задачей и не может быть решена методами решения транспортных задач из-за наличия в пунктах отправления принципиально разных вагонов с точки зрения затрат на перемещение этих вагонов в пункты назначения. Однако, эта задача может быть преобразована в другую, которая уже будет классической транспортной задачей. Идея преобразования состоит в том, чтобы реальным пунктам A1, A2,..., Am поставить в соответствие эти пункты, но с запасами a1,a2,…,am и, якобы другие, но по существу те же пункты с другими индексами Am+1, Am+2, …, Am+m с запасами a1*,a2*,…,am* и соответствующими стоимостями перемещений вагонов. Тогда вышеприведенная таблица преобразуется в таблицу
Задача, соответствующая этой таблице, уже может быть решена методами решения транспортной задачи. Пример. Решить задачу оптимального управления порожними вагонами, заданную следующей таблицей:
Здесь, как и выше, в правом верхнем углу каждой клетки, соответствующей перевозкам из Ai в Bj, стоят стоимости Cij, а в левом нижнем углу – стоимости Cij*. В столбике для запасов в каждой клетке первое слагаемое соответствует количеству имеющихся в запасе в этом пункте порожних вагонов перевозчика, а второе слагаемое – количество вагонов других форм собственности. В заявках, естественно, нет разделения по формам собственности. В соответствии с предложенным выше алгоритмом для вагонов других форм собственности из пункта A1 вводим фиктивный пункт A3, а для соответствующих вагонов из пункта A2 – фиктивный пункт A4. Кроме того, так как суммарное число заявок (140) меньше суммарного числа запасов (160), то для приведения задачи к классической транспортной задаче вводим фиктивный пункт назначения B4 с заявкой 20 (160-140=20) и с нулевыми стоимостями перевозок. Тогда задача преобразуется в задачу, представленную таблицей:
Эта задача является классической сбалансированной транспортной задачей и она может быть решена методами решения этой задачи. Начальный базисный план можем получить по методу наименьшей стоимости по строчкам. Этот план представлен нижеприведенной таблицей:
Значение критерия (стоимость перевозок) для этого базисного плана будет равно: f(Xб)=80×35+110×05+90×20+100×45+260×30+220×05+00×20=18550. Чтобы улучшить этот базисный план или убедиться, что план оптимальный, применим метод потенциалов. Выберем для пунктов отправления Ai потенциалы - ui, а для пунктов назначения Bj, соответственно, потенциалы vj. Составим систему уравнений для потенциалов, основываясь на базисных клетках предыдущей таблицы: v2 – u1 = 80, v1 – u2 = 110, v2 – u2 = 90, v3 – u2 =100, v1 – u3 =260, v1 – u4 = 220, v4 – u4 = 0.
Полагая u1 = 0, для остальных значений потенциалов из этой системы получим: v2 = 80, v1 = 100, u2 = - 10, v3 = 90, u3 = - 160, u4 = - 120, v4 = - 120. Вычислим теперь значения псевдостоимостей Ĉij = vj – ui для свободных клеток: Ĉ11 = 100, Ĉ13 = 90, Ĉ14 = - 120, Ĉ24 = - 110, Ĉ32 = 240, Ĉ33 = 250, Ĉ34 = 40, Ĉ42 = 200, Ĉ43 = 210, Ĉ44 = 0. Для всех свободных клеток, кроме трех, выполняются неравенства Ĉij ≤Cij. Для клеток (3,2), (3,3) и (3,4) имеет место противоположный знак. На основе клетки (3,2) осуществим циклическое перемещение перевозок с целью получения лучшего базисного плана. Переместим 20 единиц груза (20 вагонов) из базисной клетки (2,2) в свободную клетку (3,2), затем для соблюдения баланса из 30 вагонов клетки (3,1) 20 вагонов переместим в клетку (2,1). Цикл замкнулся. Новый базисный план, соответствующий этим перемещениям в таблице, представлен в новой таблице:
Значение критерия для этого базисного плана равно: f(Xб) = 80×35+110×25+100×45+260×10+190×20+220×05+00×20 = 17550. Как видно из значения критерия полученный базисный план лучше предыдущего плана. Проделав еще несколько итераций в методе потенциалов, получим базисный план, соответствующий таблице:
Составляя систему уравнений для потенциалов базисных клеток этой таблицы, получим: v2 – u1 = 80, v3 – u1 =90, v3 – u2 = 100, v1 – u2 = 110, v2 – u3 = 190, v1 – u4 =220, v4 – u4 = 00.
Решая эту систему, для потенциалов получим следующие значения: u1 = 0, v2 = 80, v3 =90, v1 = 100, u2 = - 10, u3 = - 110, u4 = - 120, v4 = - 120. Отсюда для псевдостоимостей свободных клеток получим: Ĉ11 = 100, Ĉ14 = - 120, Ĉ22 = 90, Ĉ24 = - 110, Ĉ31 = 220, Ĉ33 = 200, Ĉ34 = - 10, Ĉ42 = 200, Ĉ43 = 210. Нетрудно убедиться, что для всех клеток выполняются неравенства Ĉij ≤ Сij, а это означает, что полученный базисный план является оптимальным. Итак, 40вагонов, необходимых для пункта B1, доставляются в этот пункт следующим образом – 35вагонов перевозчика из пункта A2 и 5вагонов других форм собственности из этого же пункта; соответственно, 55вагонов для B2 доставляются – 25вагонов перевозчика из пункта A1 и 30вагонов других форм собственности из этого же пункта; аналогично, 45вагонов для B3 доставляются – 10вагонов перевозчика из пункта A1 и 35вагонов перевозчика из пункта A2. В фиктивный пункт назначения из-за нулевой стоимости перевозок ничего не направляется, 20 вагонов других форм собственности остаются в пункте A2. Задания В таблицах по каждому варианту представлены: запасы вагонов в пунктах Ai – в последнем столбике таблицы (в правом верхнем углу клетки-вагоны перевозчика, в левом нижнем углу клетки-вагоны других форм собственности), заявки на вагоны от пунктов Bj – в последней строке таблицы, в правом верхнем углу остальных клеток транспортные расходы по перемещению одного вагона из Ai в Bj - Cij для вагонов перевозчика, а в левом нижнем углу - Cij* для вагонов других форм собственности. Составить оптимальный план распределения вагонов. №1
№2
№3
№4
№5
№6
№7
№8
№9
№10
№11
№12
№13
№14
№15
№16
№17
№18
№19
№20
№21
№22
№23
№24
№25
Тест № 7 – Сети Петри. Справочный материал.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.200.16 (0.006 с.) |

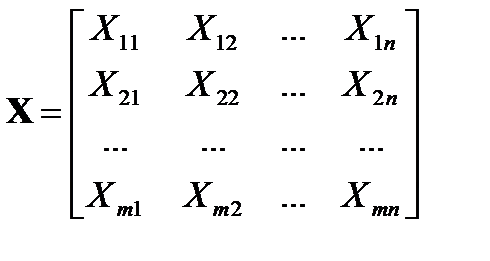 – матрица перевозок;
– матрица перевозок;


