
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное пространство. Базис.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Векторным пространством называется любое множество векторов, для элементов которого а) определена операция сложения (т.е. для каждой пары векторов b) определена операция умножения вектора на действительное число (т.е. для каждого вектора c) эти операции обладают установленными в пункте Линейные операции над векторами свойствами: 1.Для любых векторов 2. Для любых векторов 3. Для любого вектора 4. Для любого вектора
5. Для любого вектора 6. Для любого вектора 7. Для любых векторов 8. Для любого вектора
Примеры векторных пространств: V1 – множество векторов, расположенных на прямой; V2 – множество векторов, расположенных на плоскости; V3 – множество векторов, расположенных в пространстве. Базисом векторного пространства называется линейно независимая упорядоченная совокупность векторов такая, что любой вектор пространства является линейной комбинацией векторов этой системы. Размерностью векторного пространства называется количество векторов в любом его базисе. Замечание. Базисом пространства V1 векторов, расположенных на прямой, является любой ненулевой вектор этого пространства. Размерность пространства V1 равна 1. Базисом пространства V2 векторов, расположенных на плоскости, является любая пара некомпланарных векторов этого пространства. Размерность пространства V2 равна 2. Базисом пространства V3 векторов, расположенных в пространстве, является любая тройка некомпланарных векторов. Размерность пространства V3 равна 3. Пусть
называется разложением вектора Теорема. (О разложении вектора по базису). Всякий вектор может быть разложен по некоторому базису векторного пространства единственным образом. Доказательство: От противного. Рассмотрим разложение некоторого вектора
Вычитая равенства, получим Из определения 1.5.2 вытекает линейная независимость векторов Замечание. Из доказанной теоремы следует, что координаты данного вектора в заданном базисе определяются однозначно. Теорема. (Линейные операции с векторами в координатной форме). При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это же число. Доказательство: 1. Докажем первую часть теоремы, касающуюся сложения векторов. Пусть разложения векторов
Тогда
2. Аналогично получим
Следствие. Критерий коллинеарности векторов. Для того, чтобы два геометрических вектора были коллинеарными, необходимо и достаточно, чтобы их соответствующие координаты в некотором базисе были пропорциональными. Базис векторного пространства, состоящий из попарно перпендикулярных векторов единичной длины, называется ортонормированным. Замечание. Ортонормированный базис в пространстве V2 обычно обозначается
|
|||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.82.168 (0.007 с.) |

 и
и  определен третий вектор
определен третий вектор  , являющийся их суммой:
, являющийся их суммой:  определен вектор
определен вектор 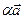 ;
; (коммутативность);
(коммутативность); (ассоциативность);
(ассоциативность); ;
; такой, что
такой, что .
. (ассоциативность);
(ассоциативность); (дистрибутивность относительно суммы скаляров);
(дистрибутивность относительно суммы скаляров); (дистрибутивность относительно суммы векторов);
(дистрибутивность относительно суммы векторов); ;
; - базис пространства V3. Представление геометрического вектора
- базис пространства V3. Представление геометрического вектора 
 называются координатами вектора
называются координатами вектора 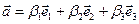 .
. .
.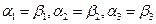 , что и требовалось доказать.
, что и требовалось доказать. .
. .
. .
. , в пространстве V3 -
, в пространстве V3 -  .
.


