
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С) Неполные уравнения плоскости.Содержание книги
Поиск на нашем сайте
Общее уравнение называется полным, если все коэффициенты его A, B, C, D отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, то уравнение называется неполным. Рассмотрим возможные виды неполных уравнений. 1) D = 0; уравнение 2) A = 0; уравнение Аналогично уравнение 3) Аналогично уравнение 4) Аналогично уравнение d) Уравнение плоскости в отрезках на осях. Рассмотрим полное уравнение. Так как в таком уравнении ни один из коэффициентов A, B, C, D не равен нулю, то его можно переписать в виде
Полагая для краткости
получаем:
e) Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой. Пусть искомая плоскость проходит через три различные точки М 1 (х 1; у 1; z 1 ), М 2 (х 2; у 2; z 2 ) и М 3 (х 3; у 3; z 3 ), не лежащие на одной прямой. Тогда векторы
Используя выражение смешанного произведения трех векторов в координатной форме, получим уравнение искомой плоскости в виде определителя
|
|||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.90 (0.01 с.) |

 определяет плоскость, проходящую через начало координат (поскольку координаты
определяет плоскость, проходящую через начало координат (поскольку координаты  начала О удовлетворяют этому уравнению).
начала О удовлетворяют этому уравнению). определяет плоскость, параллельную оси Ox (поскольку нормальный вектор этой плоскости
определяет плоскость, параллельную оси Ox (поскольку нормальный вектор этой плоскости  перпендикулярен оси Ox).
перпендикулярен оси Ox).
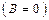 определяет плоскость, параллельную оси Oy, а уравнение
определяет плоскость, параллельную оси Oy, а уравнение 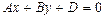
 – плоскость, параллельную оси Oz.
– плоскость, параллельную оси Oz.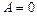 ,
,  ; уравнение
; уравнение  определяет плоскость, параллельную координатной плоскости Oxy (ибо эта плоскость параллельна осям Ox и Oy).
определяет плоскость, параллельную координатной плоскости Oxy (ибо эта плоскость параллельна осям Ox и Oy). (
( ) определяет плоскость, параллельную координатной плоскости Oxz, а уравнение
) определяет плоскость, параллельную координатной плоскости Oxz, а уравнение  (
( ; уравнение
; уравнение  , или
, или  , определяет координатную плоскость Oxy (так как плоскость
, определяет координатную плоскость Oxy (так как плоскость  (
( (
(
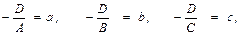

 - уравнение плоскости в отрезках на осях, так как знаменатели a, b, c есть величины отрезков, которые отсекает плоскость на осях Ox, Oy и Oz соответственно (отрезки отсчитываются от начала координат, см. рис. 11). В самом деле, точка пересечения плоскости с осью Ox определяется из уравнения этой плоскости при дополнительном условии
- уравнение плоскости в отрезках на осях, так как знаменатели a, b, c есть величины отрезков, которые отсекает плоскость на осях Ox, Oy и Oz соответственно (отрезки отсчитываются от начала координат, см. рис. 11). В самом деле, точка пересечения плоскости с осью Ox определяется из уравнения этой плоскости при дополнительном условии  , и, таким образом, величина отрезка, отсекаемого плоскостью на оси Ox, равна a. Аналогично устанавливается, что отрезки, отсекаемые плоскостью на осях Oy и Oz, имеют величины, равные соответственно b и c.
, и, таким образом, величина отрезка, отсекаемого плоскостью на оси Ox, равна a. Аналогично устанавливается, что отрезки, отсекаемые плоскостью на осях Oy и Oz, имеют величины, равные соответственно b и c.
 и
и 
 не коллинеарны, а поэтому произвольная точка M (x; y; z) лежит в одной плоскости с точками М 1, М 2 и М 3 тогда и только тогда, когда векторы
не коллинеарны, а поэтому произвольная точка M (x; y; z) лежит в одной плоскости с точками М 1, М 2 и М 3 тогда и только тогда, когда векторы  ,
, 
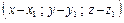 компланарны, т. е. тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю.
компланарны, т. е. тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю.



