
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных уравнений общего вида.
Если система оказалась совместной, т. е. матрицы A и`A имеют один и тот же ранг, то могут представиться две возможности: a) r = n; б) r < n. а) если r = n, то имеем n независимых уравнений с n неизвестными, причем определитель D этой системы отличен от нуля. Такая система имеет единственное решение, получаемое по формулам Крамера; б) если r < n, то число независимых уравнений меньше числа неизвестных. Перенесем лишние неизвестные x r+1, x r+2,..., x n, которые принято называть свободными, в правые части; наша система линейных уравнений примет вид: a11 x1 + a12 x2 +... + a1r xr = b1 - a1,r+1 xr+1 -... - a1nxn, a21 x1 + a22 x2 +... + a2r xr = b2 - a2,r+1 xr+1 -... - a2nxn, .............................. ar1 x1 + ar2 x2 +... + arr xr = br - ar,r+1 xr+1 -... - arnxn. Ее можно решить относительно x 1, x 2,..., x r, так как определитель этой системы (r-го порядка) отличен от нуля. Придавая свободным неизвестным произвольные числовые значения, получим по формулам Крамера соответствующие числовые значения для x 1, x 2,..., x r. Таким образом, при r < n имеем бесчисленное множество решений. Если система однородна и имеет вид: a 11 x1 + a12 x2 +... + a1n xn = 0, a21 x1 + a22 x2 +... + a2n xn = 0, .................. am1 x1 + am1 x2 +... + amn xn = 0. Из теоремы Кронекера-Капелли следует, что она всегда совместна, так как добавление столбца из нулей не может повысить ранга матрицы. Это, впрочем, видно и непосредственно – однородная система заведомо обладает нулевым, или тривиальным, решением x 1 = x2 =... = x n = 0. Пусть матрица А системы имеет ранг r. Если r = n, то нулевое решение будет единственным решением однородной системы; при r < n система обладает решениями, отличными от нулевого, и для их разыскания применяют тот же прием, как и в случае произвольной системы уравнений. Пример. Исследовать систему уравнений и решить ее, если она совместна. x1 + x2 - 2x3 - x4 + x5 =1, 3x1 - x2 + x3 + 4x4 + 3x5 =4, x1 + 5x2 - 9x3 - 8x4 + x5 =0. Решение. Будем находить ранги матриц A и `A методом элементарных преобразований, приводя одновременно систему к ступенчатому виду:
Очевидно, что r(A) = r(`A) = 2. Исходная система равносильна следующей, приведенной к ступенчатому виду: x1 + x2 - 2x3 - x4 + x5 = 1, - 4x2 + 7x3 + 7x4 = 1. Поскольку определитель при неизвестных x1 и x2 отличен от нуля, то их можно принять в качестве главных и переписать систему в виде: x1 + x2 = 2x3 + x4 - x5 + 1, - 4x2 = - 7x3 - 7x4 + 1, откуда x2 = 7/4 x3 + 7/4 x4 -1/4, x1 = 1/4 x3 -3/4 x4 - x5 + 5/4 - общее решение системы, имеющей бесчисленное множество решений. Придавая свободным неизвестным x3, x4, x5 конкретные числовые значения, будем получать частные решения. Например, при x3 = x4 = x5 = 0 x1= 5/4, x2 = - 1/4. Вектор C(5/4, - 1/4, 0, 0, 0) является частным решением данной системы.
Пример. Исследовать систему уравнений и найти общее решение в зависимости от значения параметра а. 2x1 - x2 + x3 + x4 = 1, x1 + 2x2 - x3 + 4x4 = 2, x1 + 7x2 - 4x3 + 11x4 = a. Решение. Данной системе соответствует матрица`А= x1 + 2x2 - x3 + 4x4 = 2, 5x2 - 3x3 + 7x4 = a-2, 0 = a-5. Отсюда видно, что система совместна только при a=5. Общее решение в этом случае имеет вид: x2 = 3/5 + 3/5x3 - 7/5x4, x1 = 4/5 - 1/5x3 - 6/5x4. Вопросы для самоконтроля: 1. Какая система называется однородной? 2. Какая система называется совместной? 3. Какая система называется определенной? 4. Что называется решением системы? 5. Какие системы называются равносильными? 6. Сформулируйте теоремуКронекера-Капели. 7. Перечислите основные методы решения системы линейных уравнений. 8. Укажите формулы Крамера. 9. В чем заключается матричный метод решения системы линейных уравнений? Рекомендуемая литература: 1. Михалев, А.А. Линейная алгебра и аналитическая геометрия: учебное пособие для студентов учреждений высшего проф. образования. / А.А.Михалев, И.Х.Сабитов –М.: Издательский центр «Академия», 2013 г.- 256 с. 2. Кремер, Н.Ш., Фридман, М.Н. Линейная алгебра [Электронный ресурс]: учебник и практикум / Н.Ш. Кремер, М.Н. Фридман - 2-е изд., испр. и доп. - М.: Издательство Юрайт, 2015. - URL: http://biblio-online.ru/book/EB3E86F3-26C5-43FD-BA7E-C55EA66646CA
|
|||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.253.170 (0.01 с.) |
 ~
~  ~
~  .
. . Имеем `А ~
. Имеем `А ~  ~
~ 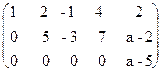 , следовательно, исходная система равносильна такой:
, следовательно, исходная система равносильна такой:


