
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные виды уравнения прямой.
а) Уравнение прямой, проходящей через данную точку в данном направлении. Пусть прямая проходит через точку М 1(х 1; у 1) и образует с осью Ох угол
Отсюда (вспоминая, что
Если бы для той же прямой мы взяли точку М (х; у) не в первом квадранте или рассмотрели бы другую прямую, у которой угол α был бы тупым, то рассуждение, естественно, усложнилось бы. Мы не будем рассматривать всех возникающих здесь возможностей. Отметим лишь, что во всех случаях получится то же уравнение. b) Уравнение прямой с угловым коэффициентом. Если мы теперь обозначим через «b» постоянную b = y 1 – kx 1, то уравнение прямой примет вид
Это уравнение называется уравнением прямой с угловым коэффициентом. В нем «b»представляет собой величину отрезка, отсекаемого данной прямой на оси Оу, начиная от начала координат. Чтобы убедиться в этом, достаточно найти координаты точки пересечения оси Оу и прямой: х = 0, у = b. Величина «b» носит название начальной ординаты прямой. Если b = 0, то получаем уравнение прямой, проходящей через начало координат
с)Уравнение пучка прямых с центром в данной точке. Совокупность лежащих на плоскости прямых, проходящих через некоторую точку этой плоскости, принято называть пучком прямых с центром в данной точке. Если в уравнении прямой угловой коэффициент k – произвольное число, то это уравнение определяет пучок прямых с центром в точке М 1(х 1; у 1), кроме прямой, перпендикулярной оси Ох и не имеющей углового коэффициента. d) Уравнение прямой, проходящей через две данные точки. Пусть даны две точки М 1(х 1; у 1), М 2(х 2; у 2) и х 1 ≠ х 2, у 1 ≠ у 2. Для составления уравнения прямой М 1 М 2 запишем уравнение пучка прямых с центром в точке М 1 в виде равенства Отсюда находим угловой коэффициент прямой по двум ее точкам:
Подставляя найденное значение k в
Записывая это же уравнение в форме
нетрудно установить, что если у 1 = у 2, то уравнение искомой прямой, параллельной оси Ох, будет
Если х 2 = х 1, то прямая параллельна оси Оу и ее уравнение
Используя в виде
или после преобразований
Это уравнение называется уравнением прямой в отрезках на осях. В этом уравнении х и у – текущие координаты, а и b – параметры. Заметим, что это уравнение удобно использовать для геометрического построения прямой. f) Уравнение прямой в полярных координатах. Зададим на плоскости согласованные декартову и полярную системы координат. Начало О декартовой системы координат поместим в полюсе, а положительную полуось Ох примем за полярную ось.
Выведем уравнение данной прямой, считая известными величины α и р. Пусть М (r; j) – произвольная точка данной прямой. Из прямоугольного треугольника ONM имеем:
g) Нормальное уравнение прямой. Перепишем уравнение
Отсюда, учитывая зависимость между декартовыми и полярными координатами точки, получим
h) Общее уравнение прямой. В предыдущих пунктах было показано, что любая прямая на плоскости в заданной декартовой прямоугольной системе координат определяется уравнением первой степени относительно переменных x и y. Установим теперь общий факт, что любую прямую без каких-либо ограничений можно задать алгебраическим уравнением первой степени. Теорема. Каждое уравнение первой степени относительно x и y вида
где А и В – коэффициенты, одновременно не равные нулю, определяет в декартовой прямоугольной системе координат некоторую прямую.
Доказательство. Рассмотрим возможные случаи. 1) А ≠ 0, В ≠ 0, С ≠ 0. Разделив все члены уравнения на В и определяя из него y, запишем уравнение в виде
Обозначая 2) В ≠ 0, С ≠ 0, А = 0. В этом случае уравнение принимает вид 3) А ≠ 0, С ≠ 0, В = 0. Уравнение принимает вид 4) А ≠ 0, В ≠ 0, С = 0. Уравнение имеет вид 5) А ≠ 0, В = 0, С = 0. Уравнение имеет вид 6) В ≠ 0, А = 0, С = 0. Уравнение имеет вид Таким образом, во всех случаях уравнение Уравнение прямой, где А и В одновременно не равны нулю, называется общим уравнением прямой.
|
||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.171.180 (0.01 с.) |
 (рис. 4). Возьмем на прямой произвольную точку М (х; у). Если провести прямые
(рис. 4). Возьмем на прямой произвольную точку М (х; у). Если провести прямые  и
и  , параллельные осям, то образуется прямоугольный треугольник
, параллельные осям, то образуется прямоугольный треугольник  .
. Ясно, что
Ясно, что 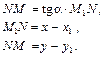
 = k) получим искомое уравнение
= k) получим искомое уравнение



 .
. , после очевидного преобразования получим уравнение прямой, проходящей через две данные точки М 1 и М 2 в виде
, после очевидного преобразования получим уравнение прямой, проходящей через две данные точки М 1 и М 2 в виде


 .
. e) Уравнение прямой в отрезках. Найдем уравнение прямой, отсекающей на оси Ох отрезок величины а (а ≠ 0), а на оси Оу – отрезок величины b, b ≠ 0.
e) Уравнение прямой в отрезках. Найдем уравнение прямой, отсекающей на оси Ох отрезок величины а (а ≠ 0), а на оси Оу – отрезок величины b, b ≠ 0. , уравнение прямой, проходящей через точки А (а; 0) и В (0; b) (рис. 5), запишем
, уравнение прямой, проходящей через точки А (а; 0) и В (0; b) (рис. 5), запишем

 Пусть дана какая-нибудь прямая, не проходящая через полюс О (рис. 6). Проведем из полюса луч ON,перпендикулярный данной прямой. Пусть α – угол между полярной осью Ох и лучом ON, p – расстояние от полюса О до данной прямой, р = | ON |.
Пусть дана какая-нибудь прямая, не проходящая через полюс О (рис. 6). Проведем из полюса луч ON,перпендикулярный данной прямой. Пусть α – угол между полярной осью Ох и лучом ON, p – расстояние от полюса О до данной прямой, р = | ON |. - уравнение прямой в полярных координатах.
- уравнение прямой в полярных координатах.
 - нормальное уравнение прямой. Числа р и α, где р – расстояние от начала О до заданной прямой, а α – угол наклона нормали ON к оси абсцисс, являются параметрами уравнения.
- нормальное уравнение прямой. Числа р и α, где р – расстояние от начала О до заданной прямой, а α – угол наклона нормали ON к оси абсцисс, являются параметрами уравнения.
 .
. ,
,  , получим уравнение
, получим уравнение  . Это уравнение прямой с угловым коэффициентом.
. Это уравнение прямой с угловым коэффициентом. , или
, или  . Это уравнение прямой, параллельной оси
. Это уравнение прямой, параллельной оси  , отсекающей на оси ординат отрезок, величина которого равна
, отсекающей на оси ординат отрезок, величина которого равна  , где
, где  , или
, или  . Это уравнение прямой, параллельной оси
. Это уравнение прямой, параллельной оси  , отсекающей от оси абсцисс отрезок, величина которого равна
, отсекающей от оси абсцисс отрезок, величина которого равна  , где
, где  .
. , или
, или  , где
, где  . Это уравнение прямой, проходящей через начало координат.
. Это уравнение прямой, проходящей через начало координат. . Это – уравнение оси ординат.
. Это – уравнение оси ординат. . Это уравнение является уравнением оси абсцисс.
. Это уравнение является уравнением оси абсцисс. является уравнением прямой линии. Тем самым теорема доказана.
является уравнением прямой линии. Тем самым теорема доказана.


