
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение матрицы и её элементов.Стр 1 из 10Следующая ⇒
Костанайский филиал Кафедра социально-гуманитарных и естественнонаучных дисциплин
УТВЕРЖДЕНО заседанием кафедры СГЕНД Протокол №__ от «__» ______ 2016 г.
КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ по дисциплине «Линейная алгебра»
Костанай, 2016 г.
Краткий конспект лекций по дисциплине «Линейная алгебра» составлен: Сизовой О.А., магистром математики, старшим преподавателем кафедры социально-гуманитарных и естественнонаучных дисциплин________________________
Краткий конспект лекций по дисциплине «Линейная алгебра» обсужден на заседании методической комиссии кафедры социально-гуманитарных и естественнонаучных дисциплин
Протокол №___ от «__» __________2016 г.
Председатель метод. комиссии __________________ И.А.Волошина
Цель: рассмотреть понятие матрицы и ее элементов, разобрать на конкретных примерах действия над матрицами; дать понятие определителя, сформулировать основные свойства определителей, рассмотреть способы вычисления определителей; сформулировать определение ранга матрицы, разобрать элементарные преобразования над матрицами, рассмотреть формулу для вычисления обратной матрицы. Ключевые слова: матрица, квадратная матрица, диагональная матрица, единичная матрица, транспонирование, определитель, минор, алгебраическое дополнение, ранг матрицы, обратная матрица. Вопросы: 1. Определение матрицы и её элементов. 2. Действия над матрицами. 3. Определитель квадратной матрицы. 4. Свойства определителей. 5. Определение ранга матрицы. 6. Элементарные преобразования матрицы. 7. Обратная матрица.
Действия над матрицами. Матрицы A и B называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны между собой. Например, матрицы Произведением матрицы A на некоторое действительное число α называется матрица αA составленная из элементов матрицы A, умноженных на число α. Из определения вытекает, что, во-первых, матрицы A и αA имеют одинаковый порядок и, во-вторых, что если все элементы некоторой матрицы имеют общий множитель, то его можно вынести за матричные скобки.
Например, 1) αA= Aα; 2) (αβ)A = α(βA) = β(αA); 3) 0A = O; 4) (αA)Т = αAТ. Пример.
Суммой двух матриц A и B одного и того же порядка называется матрица C, каждый элемент которой равен сумме соответствующих элементов матриц A и B, т.е.
Операция сложения матриц обладает следующими свойствами: 2) (A+B)+C= A+ (B + C)(ассоциативность); 3) α(A + B) = αA + αB (дистрибутивность по отношению к умножению на действительное число); 4) O + A = A; 5) (A + B)Т = AТ + BТ. Пример. Пусть Тогда А + В = Аналогично определяется вычитание матриц: А – В = Последней операцией над матрицами, которую мы рассмотрим, будет умножение матриц. Вначале сформулируем предварительное понятие. Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, если порядок матрицы A равен m × n, то порядок согласованной с ней матрицы B должен быть равен n × k (отметим, что квадратные матрицы одного порядка всегда согласованы). Перемножать можно только согласованные матрицы. Произведением двух согласованных матриц A и B называется матрица C, элементы которой рассчитываются по формуле Например, если требуется получить элемент
Число столбцов матрицы A и число строк матрицы B равны 2, значит, A и B согласованы. Тогда Пусть A - матрица - строка из 3-х элементов, а B - матрица - столбец из 3-х элементов. Тогда A и B согласованы и, в результате умножения A на B получится число. Матрицы B и A также согласованы, но в результате их умножения получится квадратная матрица 3-го порядка.
Отметим другие свойства умножения матриц. 1) Умножение матриц ассоциативно: (AB) C = A (BC). 2) Умножение матриц дистрибутивно относительно сложения: (A + B) C= AC + BC. 3) Умножение матриц коммутативно относительно умножения на действительное число: α(AB) = (αA) B = A (αB). 4) Произведение двух матриц может быть нуль - матрицей, хотя ни один из сомножителей нуль - матрицей не является. Например,
Свойства определителей. 1. Определитель не меняется при транспонировании. 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю. 3. Если в определителе переставить две строки, определитель поменяет знак. 4. Определитель, содержащий две одинаковые строки, равен нулю. 5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k. 6. Определитель, содержащий две пропорциональные строки, равен нулю. 7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j= 8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число. Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы. Определение ранга матрицы. Рассмотрим прямоугольную матрицу m x n. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k -го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение 0 £ r(A) £ min (m, n). Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k. Пример. Найти методом окаймления миноров ранг матрицы Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M2 =
6. Элементарные преобразования матрицы. Элементарными называются следующие преобразования матрицы: 1) перестановка двух любых строк (или столбцов), 2) умножение строки (или столбца) на отличное от нуля число, 3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число. Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований. Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B. Канонической матрицей называется матрица, у которой в начале При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали. Пример. Найти ранг матрицы А=
Решение. Из второй строки вычтем первую и переставим эти строки: Обратная матрица. Рассмотрим квадратную матрицу A = Обозначим D =det A. Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А·В = В·А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле А-1 = 1/D где А ij - алгебраические дополнения элементов a ij. Вычисление обратной матрицы по формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы. Пример. Для матрицы А = Решение. Находим сначала детерминант матрицы А D = det А =
Пример. Методом элементарных преобразований найти обратную матрицу для матрицы: А= Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй: Прибавим третий столбец к первому и второму: Умножим последний столбец на -1: Итак, А-1 = Вопросы для самоконтроля: 1. Дайте определение матрицы. 2. Какая матрица называется диагональной? 3. Сформулируйте понятие единичной матрицы. 4. Какие операции над матрицами вы знаете? 5. Дайте понятие квадратной матрицы. 6. Какие матрицы называются согласованными? 7. Дайте определение определителя квадратной матрицы. 8. Укажите формулы для вычисления определителей второго и третьего порядков. 9. Сформулируйте основные свойства определителя. 10. Перечислите способы вычисления определителя? 11. Дайте определение ранга матрицы. 12. Какая матрица называется канонической?
13. Сформулируйте понятие эквивалентной матрицы. 14. Какие элементарные преобразования матрицы вы знаете? 15. Укажите необходимое и достаточное условие для существования обратной матрицы. 16. Запишите формулу для вычисления обратной матрицы. Рекомендуемая литература: 1. Михалев, А.А. Линейная алгебра и аналитическая геометрия: учебное пособие для студентов учреждений высшего проф. образования. / А.А.Михалев, И.Х.Сабитов –М.: Издательский центр «Академия», 2013 г.- 256 с. 2. Кремер, Н.Ш., Фридман, М.Н. Линейная алгебра [Электронный ресурс]: учебник и практикум / Н.Ш. Кремер, М.Н. Фридман - 2-е изд., испр. и доп. - М.: Издательство Юрайт, 2015. - URL: http://biblio-online.ru/book/EB3E86F3-26C5-43FD-BA7E-C55EA66646CA Метод Гаусса. Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Теорема Кронекера-Капели. Для того, чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы. Следствие: Если ранги основной и расширенной матриц линейной системы совпадают с количеством переменных, то система имеет единственное решение. Пример. Решить систему уравнений методом Гаусса: x + y - 3z = 2, 3x - 2y + z = - 1, 2x + y - 2z = 0. Решение. Выпишем расширенную матрицу данной системы
и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13. Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим Формулы Крамера. Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель матрицы системы не равнялся 0: det A ¹ 0. Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю. Теорема. Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
Пример. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5, x1 + 2x2 - x3 + 4x4 = -2, 2x1 - 3x2 - x3 - 5x4 = -2, 3x1 + x2 +2x3 + 11 x4 = 0.
Решение. Главный определитель этой системы D = значит, система имеет единственное решение. Вычислим вспомогательные определители Di (i = D 1 = D 3 = Отсюда Матричный метод. Если матрица А системы линейных уравнений невырожденная, т.е. Пример. Решить матричным способом систему уравнений x1 - x2 + x3 = 6, 2x1 + x2 + x3 = 3, x1 + x2 +2x3 = 5. Решение. Обозначим A = Тогда данная система уравнений запишется матричным уравнением A·X=B. Поскольку D = det А-1 = 1/D Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A-1B. В данном случае A-1 = и, следовательно,
Выполняя действия над матрицами, получим:
x1 = 1/5(1×6+3×3-2×5) = 1/5 (6+9-10) = 1, x2 = 1/5 (-3×6 +1×3 - 1×5) = 1/5 (- 18 + 3 + 5) = -2, x3 = 1/5 (1×6 - 2×3 + 3×5) = 1/5 (6 -6 + 15) = 3.
Итак, С = (1, -2, 3)T. Ч.т.д. Разностью Правило вычитания векторов. Разностью векторов
Замечание. Очевидно, что
Теорема. (Критерий коллинеарности двух векторов). Для того, чтобы два вектора Доказательство: Необходимость. Пусть Достаточность. Если Ч.т.д.
Угловой коэффициент прямой. Рассмотрим любую прямую, не параллельную оси Ох (рис. 3). Обозначим через α наименьший положительный угол Если прямая параллельна оси Ох или совпадает с ней, то ее угол наклона будем считать равным нулю. Тангенс угла наклона прямой к оси Ох назовем угловым коэффициентом этой прямой и обозначим буквой k: Заметим, что если угол наклона прямой к оси Ох острый, то k > 0, если тупой, то k < 0. Для прямой, параллельной оси Ох, k = 0, а для прямой, перпендикулярной оси Ох, угловой коэффициент не существует. В последнем случае формально говорят, что угловой коэффициент равен бесконечности. В дальнейшем мы увидим, что угловой коэффициент прямой играет очень важную роль. Костанайский филиал Кафедра социально-гуманитарных и естественнонаучных дисциплин
УТВЕРЖДЕНО заседанием кафедры СГЕНД Протокол №__ от «__» ______ 2016 г.
КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ по дисциплине «Линейная алгебра»
Костанай, 2016 г.
Краткий конспект лекций по дисциплине «Линейная алгебра» составлен: Сизовой О.А., магистром математики, старшим преподавателем кафедры социально-гуманитарных и естественнонаучных дисциплин________________________
Краткий конспект лекций по дисциплине «Линейная алгебра» обсужден на заседании методической комиссии кафедры социально-гуманитарных и естественнонаучных дисциплин
Протокол №___ от «__» __________2016 г.
Председатель метод. комиссии __________________ И.А.Волошина
Цель: рассмотреть понятие матрицы и ее элементов, разобрать на конкретных примерах действия над матрицами; дать понятие определителя, сформулировать основные свойства определителей, рассмотреть способы вычисления определителей; сформулировать определение ранга матрицы, разобрать элементарные преобразования над матрицами, рассмотреть формулу для вычисления обратной матрицы. Ключевые слова: матрица, квадратная матрица, диагональная матрица, единичная матрица, транспонирование, определитель, минор, алгебраическое дополнение, ранг матрицы, обратная матрица. Вопросы: 1. Определение матрицы и её элементов. 2. Действия над матрицами. 3. Определитель квадратной матрицы. 4. Свойства определителей. 5. Определение ранга матрицы. 6. Элементарные преобразования матрицы. 7. Обратная матрица.
Определение матрицы и её элементов. Матрицы появились в середине XIX века в связи с практической потребностью решения различного рода задач, прежде всего связанных с исследованием систем линейных уравнений. Матрицей называется прямоугольная таблица вида
Матричные элементы обычно обозначаются той же буквой (только строчной), что и сама матрица, а индексы показывают место элемента матрицы в матрице: первый индекс указывает номер строки, а второй – номер столбца, на пересечении которых находится данный матричный элемент. Например, для матрицы А = Различают несколько особых случаев: 1) m =1, n >1. Матрица в этом случае называется матрицей - строкой и имеет вид
3) Если m = n, то матрица называется квадратной (порядка n).
В квадратной матрице выделяют главную диагональ (элементы, расположенные "на диагонали", проведенной из левого верхнего в правый нижний угол) и побочную диагональ (элементы, расположенные "на диагонали", проведенной из правого верхнего в левый нижний угол); 4) Если все элементы матрицы равны 0, то такая матрица называется нуль - матрицей и обозначается О.
5) Квадратная матрица порядка n называется диагональной, если все ее элементы, кроме, может быть, элементов главной диагонали равны нулю. Таким образом, матрица
6) Диагональная матрица называется единичной, если все ее диагональные элементы равны 1, т.е.
Квадратная матрица, сохраняющая свой вид при транспонировании, называется симметрической. Для симметрической матрицы справедливо соотношение AТ=A. В симметрической матрице элементы, расположенные симметрично относительно главной диагонали одинаковы. Симметрической будет, например, любая диагональная матрица. Действия над матрицами. Матрицы A и B называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны между собой. Например, матрицы Произведением матрицы A на некоторое действительное число α называется матрица αA составленная из элементов матрицы A, умноженных на число α. Из определения вытекает, что, во-первых, матрицы A и αA имеют одинаковый порядок и, во-вторых, что если все элементы некоторой матрицы имеют общий множитель, то его можно вынести за матричные скобки. Например, 1) αA= Aα; 2) (αβ)A = α(βA) = β(αA); 3) 0A = O; 4) (αA)Т = αAТ. Пример.
Суммой двух матриц A и B одного и того же порядка называется матрица C, каждый элемент которой равен сумме соответствующих элементов матриц A и B, т.е.
Операция сложения матриц обладает следующими свойствами: 2) (A+B)+C= A+ (B + C)(ассоциативность); 3) α(A + B) = αA + αB (дистрибутивность по отношению к умножению на действительное число); 4) O + A = A; 5) (A + B)Т = AТ + BТ. Пример. Пусть Тогда А + В = Аналогично определяется вычитание матриц: А – В = Последней операцией над матрицами, которую мы рассмотрим, будет умножение матриц. Вначале сформулируем предварительное понятие. Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, если порядок матрицы A равен m × n, то порядок согласованной с ней матрицы B должен быть равен n × k (отметим, что квадратные матрицы одного порядка всегда согласованы).
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.60.166 (0.199 с.) |
 и
и  отвечают данному определению и являются равными A = B. Матрица
отвечают данному определению и являются равными A = B. Матрица  не равна ни матрице A, ни матрице B, хотя она имеет те же размеры, что и A и B и состоит из тех же элементов.
не равна ни матрице A, ни матрице B, хотя она имеет те же размеры, что и A и B и состоит из тех же элементов.
 , тогда
, тогда 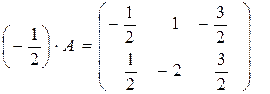

 .
. +
+  =
= 
 =
=  .
.
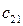 , то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы
, то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы ,
,  .
. .
. .
. ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj. .
. , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
, отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
= 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум. .
. и привести ее к каноническому виду.
и привести ее к каноническому виду. .Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
.Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:  ; из третьей строки вычтем вторую; получим матрицу В =
; из третьей строки вычтем вторую; получим матрицу В =  , которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
, которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:  .
.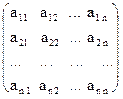 .
. ,
, найти обратную.
найти обратную. = 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D
= 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D 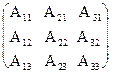 , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем:
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем:

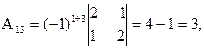





 откуда А-1 =
откуда А-1 =  .
. .
. .
. .
. .
. .
. .
. . Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А.
. Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. .
.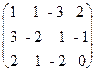
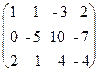 ;
; .
.
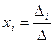 , где D = det A, а D i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
, где D = det A, а D i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
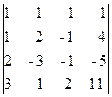 = -142 ¹ 0,
= -142 ¹ 0,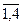 ), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при xi , столбцом из свободных членов:
), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при xi , столбцом из свободных членов: = - 142, D 2 =
= - 142, D 2 = 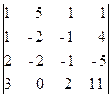 = - 284,
= - 284, = - 426, D 4 =
= - 426, D 4 = 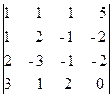 = 142.
= 142. , решение системы - вектор С=(1, 2, 3, -1)T.
, решение системы - вектор С=(1, 2, 3, -1)T.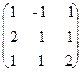 , X = (x1, x2, x3)T, B = (6, 3, 5) T.
, X = (x1, x2, x3)T, B = (6, 3, 5) T.
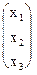 =
= 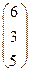 .
. двух векторов
двух векторов  и
и  назовем вектор
назовем вектор  , для которого
, для которого  .
. .
. Произведением вектора
Произведением вектора  называется вектор
называется вектор  ;
; ;
; при
при 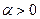 и
и  при
при  .
. , что
, что  .
. . Рассмотрим вектор
. Рассмотрим вектор  , где число
, где число  , то
, то  ; если
; если  ,то
,то  . Очевидно,
. Очевидно,  , так как
, так как  и
и  . Таким образом, мы указали число
. Таким образом, мы указали число  α
α 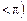 , на который надо повернуть против часовой стрелки ось Ох до совмещения с прямой, и назовем его углом наклона прямой к оси Ох.
, на который надо повернуть против часовой стрелки ось Ох до совмещения с прямой, и назовем его углом наклона прямой к оси Ох. .
.
 , составляющие матрицу, называются элементами матрицы. Матрицы обозначаются прописными буквами А, В, С, …. Для краткой записи матрицы употребляют обозначение
, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются прописными буквами А, В, С, …. Для краткой записи матрицы употребляют обозначение 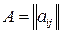

 элементы
элементы  ,
,  ….
….
 и называется матрицей - столбцом;
и называется матрицей - столбцом;

 будет диагональной.
будет диагональной.
 то транспонированной к A матрицей будет матрица
то транспонированной к A матрицей будет матрица  .
.


