
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определитель квадратной матрицы.
Для каждой квадратной матрицы вводится важная ее числовая характеристика, называемая определителем этой матрицы. Правило, по которому по элементам данной квадратной матрицы произвольного порядка вычисляется ее определитель, достаточно сложно, поэтому будем вводить это правило «постепенно», повышая порядок определителя. Пока же ограничимся таким неконструктивным определением. Каждой квадратной матрице можно по некоторому правилу поставить в соответствие число, которое называется определителем (или детерминантом) данной матрицы. Для определителя квадратной матрицы A, общий вид которой
Укажем наиболее употребительные: det A, D, D(А) или развернутое, в котором перечисляются все элементы данной матрицы
Прямые черты, заменяющие круглые (матричные) скобки, указывают на то, что имеется в виду именно определитель матрицы, т.е. единственное число, а не сама матрица A. Будем подходить к строгому определению определителя, рассмотрев это правило последовательно для определителей матриц 1-го, 2-го и 3-го порядков. Определителем матрицы 1-го порядка называется число, равное единственному имеющемуся матричному элементу этой матрицы. Определение настолько простое, что нет необходимости иллюстрировать его примером. Определитель матрицы 2-го порядка: если А= Например, Рассмотрим определитель матрицы 3-го порядка А = Для вычисления определителя именнотретьего порядка есть упрощенная формула
которая схематически (для запоминания) записывается так:
– первые три слагаемые (берутся со знаком +)
– последние 3 слагаемые (берутся со знаком −)
Пример. Найдем по упрощенной схеме определитель матрицы.
Для того чтобы определить правило вычисления определителей порядка выше, чем 3, введем сначала некоторые новые объекты. Минором элемента матрицы aij (обозначается Мij) называется значение определителя матрицы, получающейся из данной матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент (т.е. вычеркиванием i -ой строки и j -го столбца). Алгебраическим дополнением элемента матрицы aij (обозначается Аij) называется число, определяемое по формуле
Поскольку (–1) в целой степени принимает всего два значения (1 – если показатель степени есть четное число и (–1) – если нечетное), то алгебраическое дополнение элемента матрицы либо ничем не отличается от минора этого элемента (если сумма его нижних индексов – т.е. сумма номеров строки и столбца – есть четное число) или отличается от минора только знаком (если сумма нижних индексов нечетна).
Пример. Найти миноры и алгебраические дополнения всех элементов матриц А = Сначала ищем миноры всех элементов. М11= М21= М31= Учитывая формулу А11=7, А12= –13, А13=5, А21= –3, А22=5, А23= –1, А31= –5, А32=7, А33= –3 Определителем квадратной матрицы (любого порядка!) называется число, равное сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения. Для вычисления определителей матриц более высокого (чем третьего) порядка упрощенной схемы нет, поэтому используется только метод, данный в определении: выбирается строка или столбец матрицы и вычисляется сумма попарных произведений соответствующих элементов матрицы на их алгебраические дополнения. При этом вычисление алгебраических дополнений – самый трудоёмкий этап. Но поскольку строку (или столбец) можно выбирать произвольно (результат от этого не зависит), то проще выбрать ту, среди элементов которой как можно больше нулевых. При этом алгебраические дополнения нулевых элементов можно не считать, так как при составлении упомянутой выше суммы попарных произведений соответствующие слагаемые все равно обратятся в ноль. Пример. Вычислить определитель 4-го порядка: Решение. Самое большое количество нулей в любой из строк или столбцов равно 2. Поэтому для вычисления определителя выбираем любую строку или столбец с двумя нулями. Выберем, например, первый столбец (при этом говорят, что определитель будет разлагаться по первому столбцу):
Появившиеся два определителя 3-го порядка можно считать по приведенной выше упрощенной схеме. Если среди элементов матрицы нулей мало (или нет вовсе), то можно специальными действиями привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. После этого определитель легко вычисляется разложением по этой строке (столбцу). Привести определитель к такому виду помогают свойства определителей, рассмотренные ниже.
Свойства определителей. 1. Определитель не меняется при транспонировании. 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю. 3. Если в определителе переставить две строки, определитель поменяет знак. 4. Определитель, содержащий две одинаковые строки, равен нулю. 5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k. 6. Определитель, содержащий две пропорциональные строки, равен нулю. 7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j= 8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число. Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы. Определение ранга матрицы. Рассмотрим прямоугольную матрицу m x n. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k -го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение 0 £ r(A) £ min (m, n). Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k. Пример. Найти методом окаймления миноров ранг матрицы Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M2 = 6. Элементарные преобразования матрицы.
Элементарными называются следующие преобразования матрицы: 1) перестановка двух любых строк (или столбцов), 2) умножение строки (или столбца) на отличное от нуля число, 3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число. Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований. Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B. Канонической матрицей называется матрица, у которой в начале При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали. Пример. Найти ранг матрицы А=
Решение. Из второй строки вычтем первую и переставим эти строки: Обратная матрица. Рассмотрим квадратную матрицу A = Обозначим D =det A. Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0. Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А·В = В·А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В. Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле
А-1 = 1/D где А ij - алгебраические дополнения элементов a ij. Вычисление обратной матрицы по формуле для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы. Пример. Для матрицы А = Решение. Находим сначала детерминант матрицы А D = det А =
Пример. Методом элементарных преобразований найти обратную матрицу для матрицы: А= Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй: Прибавим третий столбец к первому и второму: Умножим последний столбец на -1: Итак, А-1 = Вопросы для самоконтроля: 1. Дайте определение матрицы. 2. Какая матрица называется диагональной? 3. Сформулируйте понятие единичной матрицы. 4. Какие операции над матрицами вы знаете? 5. Дайте понятие квадратной матрицы. 6. Какие матрицы называются согласованными? 7. Дайте определение определителя квадратной матрицы. 8. Укажите формулы для вычисления определителей второго и третьего порядков. 9. Сформулируйте основные свойства определителя. 10. Перечислите способы вычисления определителя? 11. Дайте определение ранга матрицы. 12. Какая матрица называется канонической? 13. Сформулируйте понятие эквивалентной матрицы. 14. Какие элементарные преобразования матрицы вы знаете? 15. Укажите необходимое и достаточное условие для существования обратной матрицы. 16. Запишите формулу для вычисления обратной матрицы. Рекомендуемая литература: 1. Михалев, А.А. Линейная алгебра и аналитическая геометрия: учебное пособие для студентов учреждений высшего проф. образования. / А.А.Михалев, И.Х.Сабитов –М.: Издательский центр «Академия», 2013 г.- 256 с.
2. Кремер, Н.Ш., Фридман, М.Н. Линейная алгебра [Электронный ресурс]: учебник и практикум / Н.Ш. Кремер, М.Н. Фридман - 2-е изд., испр. и доп. - М.: Издательство Юрайт, 2015. - URL: http://biblio-online.ru/book/EB3E86F3-26C5-43FD-BA7E-C55EA66646CA
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 1021; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.233.58 (0.046 с.) |
 применяются различные обозначения.
применяются различные обозначения.

 , то
, то 
 .
. .
. ,
,

 .
.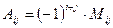
 .
. , М12=
, М12=  , М13=
, М13=  ,
, , М22=
, М22=  , М23=
, М23=  ,
, , М32=
, М32=  , М33=
, М33=  .
. .
. .
. ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj. .
. , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно
, отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М2. Их всего два (можно = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
= 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум. .
. и привести ее к каноническому виду.
и привести ее к каноническому виду. .Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
.Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:  ; из третьей строки вычтем вторую; получим матрицу В =
; из третьей строки вычтем вторую; получим матрицу В =  , которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
, которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:  .
.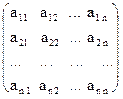 .
. ,
, найти обратную.
найти обратную. = 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D
= 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D 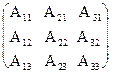 , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем:
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем:

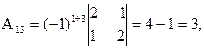





 откуда А-1 =
откуда А-1 =  .
. .
. .
. .
. .
. .
. .
. . Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А.
. Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. .
.


