
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон пуассона – закон редких событий
Пусть требуется найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность осуществления события В этом случае ни формула Бернулли, ни асимптотическая формула Лапласа не могут быть практически использованы для решения поставленной задачи. При больших
Формула Пуассона широко используется в теории массового обслуживания. Простейший поток событий Определение. Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени (в предельном случае, если события следуют через определенные интервалы). Вероятность появления
Примеры решения задач: Задача 1. Из ящика, где было 4 лопнувших и 12 целых пробирок, вынуто наугад 3 пробирки. Какова вероятность того, что две из них целые? Решение: Число способов, которыми можно извлечь Найдем число исходов, благоприятствующих интересующему нас событию: среди
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов
Вычисления:
Ответ: вероятность того, что из 3 наудачу взятых пробирок 2 целые равна Задача 2. Центральная городская аптека закреплена за тремя больницами. Вероятность того, что в течение рабочего дня придется отпустить медикаменты первой больнице, равна 0,6, второй больнице – 0,2, третьей – 0,4. Какова вероятность того, что в течение рабочего дня придется отпустить медикаменты: 1) одной больнице? 2) по крайней мере, двум больницам?
Решение: Пусть событие
вероятность противоположного события
событие
вероятность противоположного события
событие
вероятность противоположного события
1) Событие
Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий:
2) Событие
Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий:
Ответ: 1) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты одной больнице, равна Задача 3. В цехе установлено 5 датчиков предельно допустимой концентрации пыли в воздухе, каждый из которых может включать систему сигнализации. Вероятность срабатывания первого датчика равна 0,8, второго – 0,9, третьего – 0,85, четвертого – 0,7, пятого – 0,75. 1) Найти вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает? 2) Сигнализация сработала. Какова вероятность того, что сигнализацию включил третий датчик? Решение: Пусть событие
Известны условные вероятности события
1) Вероятность события
3) Событие
Ответ: 1) вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает, равна Задача 4. Вероятность заражения желудочно-кишечными заболеваниями при однократном приеме внутрь 250 мл не кипяченой речной воды составляет 0,1. Какова вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, если все они выпили по 250 мл не кипяченой речной воды? Решение: События – заражение желудочно-кишечными заболеваниями относятся к повторным независимым испытаниям. Вероятность того, что некоторое событие
По условию: Известно, что сумма вероятностей событий, составляющих полную систему, равна 1, т.е. тогда получаем, что Вычислим
Ответ: вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, равна Задача 5. Какова вероятность того, что в партии таблеток, насчитывающей 10000 штук, 1) не более 20 окажутся нестандартными, если вероятность того, что отдельная таблетка окажется нестандартной, составляет 0,0012? 2) ровно 12 штук окажутся нестандартными? Решение: События – нестандартная таблетка – относятся к повторным независимым испытаниям. Число испытаний ( 1) Для ответа на первый вопрос используем формулу, позволяющую приближённо определять вероятность По условию: Анализ условия показывает, что
здесь
По таблице значений функции
2) Для ответа на второй вопрос используем формулу, позволяющую приближённо определять вероятность По условию: Вычисляем
По таблице значений функции Тогда Ответ: 1) вероятность того, что в партии таблеток из 10000 штук, не более 20 окажутся нестандартными, равна Задача 6. Среднее число самолетов, прибывших в аэропорт за 1 минуту, равно 3. Найти вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов; б) не более 2; в) 4 самолета. Решение: События – прибытия самолетов в аэропорт – представляют собой простейший поток событий. Вероятность появления
По условию: а) Или в данном случае: Вычисляем:
б) в) Ответ: вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов, равна
|
|||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.4.65 (0.043 с.) |
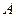 очень мала, событие
очень мала, событие  раз.
раз.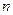 , малых
, малых  и если выполняется условие
и если выполняется условие  , то для вычисления искомой вероятности применяют формулу Пуассона (закон Пуассона):
, то для вычисления искомой вероятности применяют формулу Пуассона (закон Пуассона): , где
, где  .
. определяется формулой Пуассона:
определяется формулой Пуассона: , где
, где – интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени.
– интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени. пробирки из их общего числа
пробирки из их общего числа  , равно
, равно  – числу сочетаний из
– числу сочетаний из  элементов по
элементов по  целые.
целые.  целых
целых  различными способами; при этом
различными способами; при этом  пробирок должны быть лопнувшими, взять же
пробирок должны быть лопнувшими, взять же  имеющихся можно
имеющихся можно  различными способами. Следовательно, число благоприятствующих исходов равно
различными способами. Следовательно, число благоприятствующих исходов равно .
. :
: .
. ,
, ,
, ,
, .
. .
. ,
, – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна ;
; состоит в том, что аптеке придется отпустить медикаменты второй больнице; вероятность этого события по условию равна
состоит в том, что аптеке придется отпустить медикаменты второй больнице; вероятность этого события по условию равна ,
, – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна ;
; состоит в том, что аптеке придется отпустить медикаменты третьей больнице; вероятность этого события по условию равна
состоит в том, что аптеке придется отпустить медикаменты третьей больнице; вероятность этого события по условию равна ,
, – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна .
. – аптеке придется отпустить медикаменты одной аптеке – реализуется следующим образом:
– аптеке придется отпустить медикаменты одной аптеке – реализуется следующим образом: .
.

 – аптеке придется отпустить лекарство, по крайней мере, двум (т.е. двум или трем) больницам – включает в себя следующие события:
– аптеке придется отпустить лекарство, по крайней мере, двум (т.е. двум или трем) больницам – включает в себя следующие события: .
. , или
, или .
. ; 2) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты, по крайней мере, двум больницам, равна
; 2) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты, по крайней мере, двум больницам, равна  .
. – включение
– включение  датчиком сигнализации. Вероятности событий
датчиком сигнализации. Вероятности событий  по условию одинаковы и равны
по условию одинаковы и равны  . События
. События  .
. – вероятности срабатывания
– вероятности срабатывания  датчика:
датчика:
 ,
,  ,
,  ,
,  ,
,  .
. , или
, или  .
. ) найдем по формуле Байеса:
) найдем по формуле Байеса: , или
, или .
. ; 2) вероятность того, что сигнализацию при этом включил третий датчик, равна
; 2) вероятность того, что сигнализацию при этом включил третий датчик, равна  .
. .
.
 ,
, 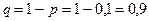 ,
,  (событие – «хотя бы один» – означает «один и более»), т.е.
(событие – «хотя бы один» – означает «один и более»), т.е.  .
. . Для данного случая имеем:
. Для данного случая имеем:  или
или  ,
, .
. :
: .
. .
. ) в данном случае велико, поэтому использование формулы Бернулли для нахождения вероятности
) в данном случае велико, поэтому использование формулы Бернулли для нахождения вероятности  приводит к вычислительным трудностям.
приводит к вычислительным трудностям. , с которой происходит событие
, с которой происходит событие  ,
,  ,
,  ,
,  .
. , значит, для вычисления вероятности
, значит, для вычисления вероятности  используем интегральную теорему Лапласа:
используем интегральную теорему Лапласа: ,
, – стандартный интеграл вероятностей (функция Лапласа),
– стандартный интеграл вероятностей (функция Лапласа),  ,
,  , причем
, причем  . Таким образом, получаем:
. Таким образом, получаем: .
. находим (Приложение 2), что
находим (Приложение 2), что  , тогда вероятность
, тогда вероятность .
. , где
, где  ,
,  (локальная теорема Лапласа).
(локальная теорема Лапласа). ,
,  :
: .
. находим (Приложение 1), что
находим (Приложение 1), что  .
. .
. ; 2) вероятность того, что в партии таблеток из 10000 штук, ровно 12 окажутся нестандартными, равна
; 2) вероятность того, что в партии таблеток из 10000 штук, ровно 12 окажутся нестандартными, равна  .
. , где
, где ,
,  :
: , т.е.
, т.е.  . Для полной системы событий имеем:
. Для полной системы событий имеем:  . Тогда интересующая нас вероятность
. Тогда интересующая нас вероятность  .
. ,
,  ,
,  ,
, 
 ;
; , т.е.
, т.е.  . Согласно теореме сложения вероятностей получаем, что
. Согласно теореме сложения вероятностей получаем, что  . Воспользуемся вычислениями, сделанными в предыдущем пункте, и получим, что
. Воспользуемся вычислениями, сделанными в предыдущем пункте, и получим, что  ;
; . В данном случае искомая вероятность
. В данном случае искомая вероятность  вычисляется по формуле Пуассона:
вычисляется по формуле Пуассона:  .
. ; б) не более 2, равна
; б) не более 2, равна  ; в) 4 самолета, равна
; в) 4 самолета, равна  .
.


