
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З. А. Филимонова, Е. О. ПлешаковаСтр 1 из 13Следующая ⇒
З.А.Филимонова, Е.О.Плешакова ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Контрольные задания и методические указания для студентов заочной формы обучения направления подготовки Менеджмент
Учебно-методическое пособие
Волгоград 2016 УДК 519.2 (075.8) ББК 22.171 я73 Ф 53
Авторы: З.А.Филимонова – заведующая кафедрой математики и информатики ВолгГМУ Е.О.Плешакова – доцент кафедры математики и информатики ВолгГМУ
Рецензенты: зав.кафедрой физики ГБОУ ВПО «Волгоградский государственный медицинский университет», к.п.н., доцент С.А.Коробкова, профессор кафедры информатики и математики ЧОУ ВО «Волгоградский институт бизнеса», д.ф.-м.н., профессор М.Б.Белоненко
Печатается по решению ЦМС ГБОУ ВПО ВолгГМУ (протокол №___ от ____________)
Филимонова З.А. Ф53 Теория вероятностей и математическая статистика. Контрольные задания и методические указания для студентов заочной формы обучения направления подготовки Менеджмент: Учебно-методическое пособие. / З.А.Филимонова, Е.О.Плешакова – Волгоград: Изд-во ВолгГМУ, 2016. – 87 с.
Пособие содержит справочный теоретический материал по таким разделам как теория вероятностей случайных события, теория вероятностей случайных величин, элементы математической статистики, статистическая проверка статистических гипотез, статистические методы анализа, основы теории временных рядов и теории оптимизации, методический материал по изучению данных разделов, а также достаточно большой объем типовых задач, приводимых с решениями. Учебно-методическое пособие подготовлено для студентов заочной формы обучения направления подготовки «Менеджмент» и разработано в соответствии с курсом «Теория вероятностей и математическая статистика» и с учетом требований ФГОС ВО.
© Изд-во ВолгГМУ, 2016 © З.А.Филимонова – 2016 ОГЛАВЛЕНИЕ
ТАБЛИЦА ВАРИАНТОВ КОНТРОЛЬНОЙ РАБОТЫ
НЕОБХОДИМЫЕ СВЕДЕНИЯ И РЕКОМЕНДАЦИИ ВВЕДЕНИЕ Настоящие методические указания предназначены в помощь студентам-заочникам при изучении дисциплины «Теория вероятностей и математическая статистика». В них приведены основные теоретические вопросы курса. По каждому вопросу даются подробные разъяснения, и приводится достаточное количество разобранных задач, иллюстрирующих применение теории к решению типовых задач, а также указана учебная литература для самостоятельного изучения. В соответствии с учебным планом студенты-заочники слушают лекции (4 часа), выполняют лабораторные и практические задания (2+2 час), самостоятельно выполняют контрольную работу по Теории вероятностей и математической статистике (119 час), и сдают экзамен.
Студента 2 курса заочного отделения направления подготовки Менеджмент Волгоградского государственного медицинского университета Фамилия, имя, отчество (полностью) № зачётной книжки ____________ Домашний адрес: _________________________ Дата отправки ________
Прорецензированную зачтённую контрольную работу вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, студент должен представить при сдаче экзамена. В противном случае студент к сдаче экзамена не допускается. При сдаче экзамена студент должен показать: а) чёткое знание математических определений и формул, предусмотренных программой, и умение обосновать их (доказательство теорем, вывод формул);
б) умение точно и сжато выражать математическую мысль (в особенности при формулировке теорем и определений); в) умение применять приобретенные навыки по дисциплине к решению задач (при оценке решения учитывается, насколько быстро приводят к цели применяемые средства, и в какой мере автор решения умеет его обосновывать). 2 Основные теоретические вопросы курса 1. Множество элементарных событий. Случайные события и их классификация. Полная группа событий. Частота событий и ее свойство статистической устойчивости. Классическое и статистическое определения вероятности случайного события. Аксиомы теории вероятностей и следствие из них. 2. Основные теоремы теории вероятностей. 3. Случайная величина как математическая модель вероятностного явления. Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины, многоугольник распределения. Функции распределения и функции плотности распределения вероятностей случайных величин и их свойства. 4. Распределение Бернулли, распределение Пуассона. Локальная и интегральная теоремы Муавра-Лапласса. 5. Числовые характеристики дискретной случайной величины и их свойства. 6. Функция распределения и плотность вероятности НСВ. Числовые характеристики непрерывной случайной величины. Нормальный закон распределения. Вероятность попадания значения нормально распределенной СВ в заданный интервал. Правило «трех сигм». 7. Неравенство Чебышева. Дисперсионная и корреляционная матрицы случайного вектора. Ковариация и коэффициент корреляции двух случайных величин. 8. Предельные теоремы в теории вероятностей. Закон больших чисел, теорема Чебышева. Центральная предельная теорема для одинаково распределенных независимых случайных величин, центральная теорема Муавра-Лапласа, как ее следствие. 9. Оценивание скорости сходимости частоты к вероятности в схеме независимых испытаний Бернулли, сравнение результатов использования неравенства Чебышева и интегральной теоремы Муавра-Лапласа. 11. Основные задачи математической статистики. Генеральная и выборочная совокупности. Репрезентативность выборки. Статистическое распределение выборки, дискретные и интервальные вариационные ряды, полигон, гистограмма. Эмпирическая функция распределения вероятностей. 12. Оценки числовых характеристик распределения по данным распределения. Точечные оценки параметров распределения. Генеральная средняя и выборочная средняя. Генеральная дисперсия и выборочная дисперсия. 13. Несмещенная и смещенная оценки генеральной дисперсии: выборочная и исправленная выборочная дисперсии. Доверительный интервал и доверительная вероятность. Нахождение границ доверительного интервала для оценки математического ожидания нормально распределенной случайной величины по данным выборки малого объема. Распределение Стьюдента. Статистическая проверка статистических гипотез. Нулевая и конкурирующая гипотезы. 14. Критерии согласия, критерии однородности, критерии независимости, критерии значимости, знаковый анализ, ранговый анализ в задачах анализа данных. 15. Коэффициенты ранговой корреляции Спирмена и Кендалла, коэффициент конкордации.
16. Модели и методы непараметрической статистики. 17. Элементы дисперсионного и корреляционного анализов. Понятие кластер-анализа 18. Элементы теории временных (динамических) рядов. 19. Задачи оптимизации в здравоохранении (оптимизация планов обследования, перевозок и т.д.). Понятие о линейном программировании. Понятие о целевой функции. Испытание и событие В природе и повседневной жизни часто приходится сталкиваться со случайными явлениями, т. е. с ситуациями, исход которых нельзя точно предвидеть. Процесс познания действительности в этом случае осуществляется в результате наблюдений или испытаний (экспериментов). Определение. Под испытанием (наблюдением) понимается любой доступный частому повторению процесс, протекающий при реализации заданного комплекса условий. Определение. Результат, или исход испытания называется событием. Виды событий Различают три вида событий: случайные, достоверные и невозможные. Определение. Событие, которое при реализации заданного комплекса условий может произойти, а может и не произойти, называется случайным. Определение. Событие, которое неизбежно происходит при каждой реализации заданного комплекса условий, называется достоверным. Определение. Событие, которое заведомо не может произойти при реализации заданного комплекса условий, называется невозможным. Виды случайных событий Случайные события подразделяются на следующие виды: равновозможные, несовместные и совместные, зависимые и независимые. Определение. Два или несколько случайных событий называются равновозможными, если условия их появления одинаковы и нет основания утверждать, что какое-либо из них в результате испытания имеет больше шансов осуществиться, чем другие. Определение. События называются несовместными, если в результате испытания осуществление одного из них исключает осуществление остальных. Определение. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Определение. Два события называются независимыми, если появление одного из них не влияет на шансы появления другого. Определение. Два события называются зависимыми, если появление одного из них влияет на шансы появления другого. Полная группа событий Определение. Если в результате испытания обязательно осуществится одно и только одно из несовместных событий
Определение. Два несовместных события, образующие полную группу событий, называются противоположными. Исходы испытания Определение. Несовместные события, имеющие одинаковую возможность осуществиться, называются исходами испытания. Определение. Исходы Операции над событиями Определение. Если при каждом осуществлении заданного комплекса условий, при котором происходит событие Определение. Если Определение. Событие, состоящее в наступлении обоих событий Определение. Событие, состоящее в наступлении хотя бы одного из событий Событие, противоположное событию Определение суммы и произведения двух событий обобщается на любое число событий. Понятие вероятности Вычисление вероятностей Формула полной вероятности Пусть событие Пусть известны вероятности Теорема. Вероятность события Данную формулу называют формулой полной вероятности. Формула Бейеса Пусть событие
Таким образом, вероятность гипотезы после опыта равна дроби, числителем которой является произведение вероятности этой гипотезы до опыта на вероятность события по этой гипотезе, а знаменателем – сумма таких же произведений для всех возможных в данном случае гипотез (или полная вероятность события
Локальная теорема Лапласа Теорема. Вероятность того, что в
Таблица для положительных значений функции Гаусса Простейший поток событий Определение. Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени (в предельном случае, если события следуют через определенные интервалы). Вероятность появления
Примеры решения задач: Задача 1. Из ящика, где было 4 лопнувших и 12 целых пробирок, вынуто наугад 3 пробирки. Какова вероятность того, что две из них целые? Решение: Число способов, которыми можно извлечь Найдем число исходов, благоприятствующих интересующему нас событию: среди
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов
Вычисления:
Ответ: вероятность того, что из 3 наудачу взятых пробирок 2 целые равна Задача 2. Центральная городская аптека закреплена за тремя больницами. Вероятность того, что в течение рабочего дня придется отпустить медикаменты первой больнице, равна 0,6, второй больнице – 0,2, третьей – 0,4. Какова вероятность того, что в течение рабочего дня придется отпустить медикаменты: 1) одной больнице? 2) по крайней мере, двум больницам? Решение: Пусть событие
вероятность противоположного события
событие
вероятность противоположного события
событие
вероятность противоположного события
1) Событие
Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий:
2) Событие
Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий:
Ответ: 1) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты одной больнице, равна Задача 3. В цехе установлено 5 датчиков предельно допустимой концентрации пыли в воздухе, каждый из которых может включать систему сигнализации. Вероятность срабатывания первого датчика равна 0,8, второго – 0,9, третьего – 0,85, четвертого – 0,7, пятого – 0,75. 1) Найти вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает? 2) Сигнализация сработала. Какова вероятность того, что сигнализацию включил третий датчик? Решение: Пусть событие Известны условные вероятности события
1) Вероятность события
3) Событие
Ответ: 1) вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает, равна Задача 4. Вероятность заражения желудочно-кишечными заболеваниями при однократном приеме внутрь 250 мл не кипяченой речной воды составляет 0,1. Какова вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, если все они выпили по 250 мл не кипяченой речной воды? Решение: События – заражение желудочно-кишечными заболеваниями относятся к повторным независимым испытаниям. Вероятность того, что некоторое событие
По условию: Известно, что сумма вероятностей событий, составляющих полную систему, равна 1, т.е. тогда получаем, что Вычислим
Ответ: вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, равна Задача 5. Какова вероятность того, что в партии таблеток, насчитывающей 10000 штук, 1) не более 20 окажутся нестандартными, если вероятность того, что отдельная таблетка окажется нестандартной, составляет 0,0012? 2) ровно 12 штук окажутся нестандартными? Решение: События – нестандартная таблетка – относятся к повторным независимым испытаниям. Число испытаний ( 1) Для ответа на первый вопрос используем формулу, позволяющую приближённо определять вероятность По условию: Анализ условия показывает, что
здесь
По таблице значений функции
2) Для ответа на второй вопрос используем формулу, позволяющую приближённо определять вероятность По условию: Вычисляем
По таблице значений функции Тогда Ответ: 1) вероятность того, что в партии таблеток из 10000 штук, не более 20 окажутся нестандартными, равна Задача 6. Среднее число самолетов, прибывших в аэропорт за 1 минуту, равно 3. Найти вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов; б) не более 2; в) 4 самолета. Решение: События – прибытия самолетов в аэропорт – представляют собой простейший поток событий. Вероятность появления
По условию: а) Или в данном случае: Вычисляем:
б) в) Ответ: вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов, равна
Решение 1) По известной вероятности попадания
или или
или
По таблице значений функции следовательно, 2) Вероятность попадания
По таблице значений функции Выборочные характеристики Характеристики положения Определение. Выборочной средней называется среднее арифметическое значение вариант статистического ряда. Вычисляется по формуле:
Определение. Модой В дискретном вариационном ряду мода – варианта, встречающая с наибольшей частотой.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.81.206 (0.16 с.) |

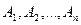 , то эти события называются полной группой событий.
, то эти события называются полной группой событий. называются благоприятными для события
называются благоприятными для события 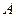 , если осуществление любого из исходов
, если осуществление любого из исходов  , то говорят, что
, то говорят, что 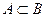 или
или  .
. .
.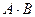 или
или  .
. или
или 
 .
.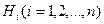 из полной группы несовместных событий
из полной группы несовместных событий 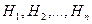 . Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.
. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. этих гипотез и условные вероятности
этих гипотез и условные вероятности 
 события А. Требуется найти вероятность события
события А. Требуется найти вероятность события  , равна сумме произведений вероятностей каждой из этих гипотез на соответствующую условную вероятность события
, равна сумме произведений вероятностей каждой из этих гипотез на соответствующую условную вероятность события  .
. )
) 
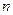 независимых испытаниях, в каждом из которых вероятность осуществления события
независимых испытаниях, в каждом из которых вероятность осуществления события  , событие
, событие  раз, приближённо равна (тем точнее, чем больше
раз, приближённо равна (тем точнее, чем больше  , где
, где  ,
,  .
. приведена в Приложение 1 данного пособия. Поскольку функция
приведена в Приложение 1 данного пособия. Поскольку функция  , то для отрицательных значений аргумента пользуются этой же таблицей.
, то для отрицательных значений аргумента пользуются этой же таблицей. определяется формулой Пуассона:
определяется формулой Пуассона: , где
, где – интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени.
– интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени. пробирки из их общего числа
пробирки из их общего числа  , равно
, равно  – числу сочетаний из
– числу сочетаний из  элементов по
элементов по  целые.
целые.  целых
целых  различными способами; при этом
различными способами; при этом  пробирок должны быть лопнувшими, взять же
пробирок должны быть лопнувшими, взять же  имеющихся можно
имеющихся можно  различными способами. Следовательно, число благоприятствующих исходов равно
различными способами. Следовательно, число благоприятствующих исходов равно .
. :
: .
. ,
, ,
, ,
, .
. .
. ,
, – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна ;
; состоит в том, что аптеке придется отпустить медикаменты второй больнице; вероятность этого события по условию равна
состоит в том, что аптеке придется отпустить медикаменты второй больнице; вероятность этого события по условию равна ,
, – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна ;
; состоит в том, что аптеке придется отпустить медикаменты третьей больнице; вероятность этого события по условию равна
состоит в том, что аптеке придется отпустить медикаменты третьей больнице; вероятность этого события по условию равна ,
, – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна .
. – аптеке придется отпустить медикаменты одной аптеке – реализуется следующим образом:
– аптеке придется отпустить медикаменты одной аптеке – реализуется следующим образом: .
.

 – аптеке придется отпустить лекарство, по крайней мере, двум (т.е. двум или трем) больницам – включает в себя следующие события:
– аптеке придется отпустить лекарство, по крайней мере, двум (т.е. двум или трем) больницам – включает в себя следующие события: .
. , или
, или .
. ; 2) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты, по крайней мере, двум больницам, равна
; 2) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты, по крайней мере, двум больницам, равна  .
. – включение
– включение  датчиком сигнализации. Вероятности событий
датчиком сигнализации. Вероятности событий  по условию одинаковы и равны
по условию одинаковы и равны  . События
. События  .
. – вероятности срабатывания
– вероятности срабатывания  датчика:
датчика: ,
,  ,
,  ,
,  ,
,  .
. .
. ) найдем по формуле Байеса:
) найдем по формуле Байеса: , или
, или .
. ; 2) вероятность того, что сигнализацию при этом включил третий датчик, равна
; 2) вероятность того, что сигнализацию при этом включил третий датчик, равна  .
. .
.
 ,
, 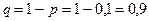 ,
,  (событие – «хотя бы один» – означает «один и более»), т.е.
(событие – «хотя бы один» – означает «один и более»), т.е.  .
. . Для данного случая имеем:
. Для данного случая имеем:  или
или  ,
, .
. :
: .
. .
. ) в данном случае велико, поэтому использование формулы Бернулли для нахождения вероятности
) в данном случае велико, поэтому использование формулы Бернулли для нахождения вероятности  приводит к вычислительным трудностям.
приводит к вычислительным трудностям. , с которой происходит событие
, с которой происходит событие  ,
,  ,
,  ,
,  .
. , значит, для вычисления вероятности
, значит, для вычисления вероятности  используем интегральную теорему Лапласа:
используем интегральную теорему Лапласа: ,
, – стандартный интеграл вероятностей (функция Лапласа),
– стандартный интеграл вероятностей (функция Лапласа),  ,
,  , причем
, причем  . Таким образом, получаем:
. Таким образом, получаем: .
. находим (Приложение 2), что
находим (Приложение 2), что  , тогда вероятность
, тогда вероятность .
. ,
,  :
: .
. находим (Приложение 1), что
находим (Приложение 1), что  .
. .
. ; 2) вероятность того, что в партии таблеток из 10000 штук, ровно 12 окажутся нестандартными, равна
; 2) вероятность того, что в партии таблеток из 10000 штук, ровно 12 окажутся нестандартными, равна  .
. , где
, где ,
,  :
: , т.е.
, т.е.  . Для полной системы событий имеем:
. Для полной системы событий имеем:  . Тогда интересующая нас вероятность
. Тогда интересующая нас вероятность  .
. ,
,  ,
,  ,
, 
 ;
; , т.е.
, т.е.  . Согласно теореме сложения вероятностей получаем, что
. Согласно теореме сложения вероятностей получаем, что  . Воспользуемся вычислениями, сделанными в предыдущем пункте, и получим, что
. Воспользуемся вычислениями, сделанными в предыдущем пункте, и получим, что  ;
; . В данном случае искомая вероятность
. В данном случае искомая вероятность  вычисляется по формуле Пуассона:
вычисляется по формуле Пуассона:  .
. ; б) не более 2, равна
; б) не более 2, равна  ; в) 4 самолета, равна
; в) 4 самолета, равна  .
. в заданный интервал найдем среднеквадратическое отклонение
в заданный интервал найдем среднеквадратическое отклонение  . Для этого воспользуемся формулой
. Для этого воспользуемся формулой  . Согласно условию
. Согласно условию  ,
,  , т.е.
, т.е.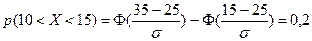
 ,
, ,
, .
.
 находим (Приложение 2), что
находим (Приложение 2), что 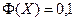 , если
, если  ,
, .
.
 , а вероятность
, а вероятность  .
.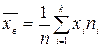 .
. называется наиболее часто встречающая в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда.
называется наиболее часто встречающая в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда.


