
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики дискретной случайной величины
Математическое ожидание Определение. Математическим ожиданием Свойства математического ожидания 1. Математическое ожидание постоянной величины равно самой постоянной: 2. Математическое ожидание алгебраической суммы нескольких случайных величин равно алгебраической сумме математических ожиданий этих величин: Следствие. Если 3. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин: Следствие. Постоянный множитель можно выносить за знак математического ожидания: 4. Математическое ожидание Дисперсия Определение. Дисперсией
Для вычисления дисперсии также можно использовать следующую формулу:
т.е. дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом её математического ожидания. Свойства дисперсии 1. Дисперсия постоянной величины равна нулю: 2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: 3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин: 4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин: 5. Если Замечание 2. Для вычисления дисперсии биноминального распределения можно воспользоваться следующей формулой: Среднеквадратическое отклонение Определение. Среднеквадратическим отклонением случайной величины называется квадратный корень из дисперсии:
Замечание 3. На основании данного определения для обозначения дисперсии часто используется символ
Интегральная функция распределения Для количественной характеристики распределения случайной величины Определение. Интегральной функцией распределения называют функцию
Свойства функции распределения 1. Значения интегральной функции распределения принадлежат отрезку 2. Функция распределения есть неубывающая функция, т. е. если Следствие 1. Вероятность того, что случайная величина Следствие 2. Вероятность того, что непрерывная случайная величина 3. Если возможные значения случайной величины Следствие 3. Если возможные значения случайной величины Для дискретной случайной величины функция распределения определяется по формуле: Дифференциальная функция распределения Непрерывную случайную величину можно задавать не только с помощью интегральной функции, но и с использованием дифференциальной функции распределения вероятностей. Определение. Дифференциальной функцией распределения
Часто вместо термина «дифференциальная функция» пользуются термином «дифференциальный закон распределения» или термином «плотность вероятности». Так как интегральная функция является первообразной дифференциальной функции, то вероятность того, что непрерывная случайная величина Свойства дифференциальной функции распределения
1. Дифференциальная функция распределения есть функция неотрицательная: 2. Несобственный интеграл от дифференциальной функции распределения равен Последнее равенство называется условием нормировки плотности вероятностей.
|
||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.233 (0.007 с.) |
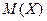 дискретной случайной величины
дискретной случайной величины  называется сумма произведений всех возможных ее значений на соответствующие им вероятности:
называется сумма произведений всех возможных ее значений на соответствующие им вероятности: 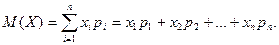
 , где
, где 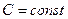 .
.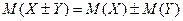 .
.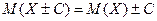 .
.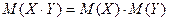 .
.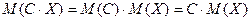 , где
, где 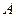 в
в 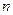 независимых испытаниях (математическое ожидание биноминального распределения) равно произведению числа испытаний на вероятность появления события в каждом испытании:
независимых испытаниях (математическое ожидание биноминального распределения) равно произведению числа испытаний на вероятность появления события в каждом испытании: 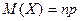 .
.
 дискретной случайной величины
дискретной случайной величины 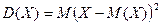 .
.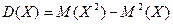 ,
,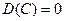 ,
, 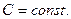
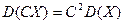 ,
, 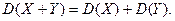
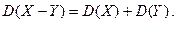
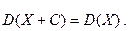
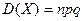 , где
, где 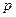 – вероятность осуществления события
– вероятность осуществления события 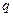 – вероятность осуществления события
– вероятность осуществления события  (противоположного событию
(противоположного событию 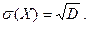
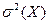 .
. случайной величины.
случайной величины.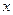 , т. е.
, т. е.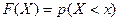 .
.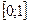 .
.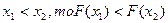 .
.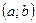 , равна приращению её интегральной функции распределения на интервале
, равна приращению её интегральной функции распределения на интервале 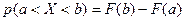 .
.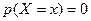 .
.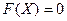 при
при 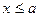 ,
, 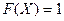 при
при 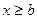 .
.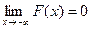 ,
, 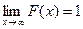 .
.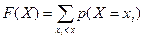 , где неравенство
, где неравенство  под знаком суммы указывает, что суммирование распространяется на все значения
под знаком суммы указывает, что суммирование распространяется на все значения 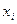 , меньшие
, меньшие 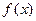 называется производная от интегральной функции:
называется производная от интегральной функции: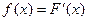 .
. примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 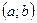 , определяется равенством:
, определяется равенством: 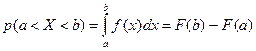 . Если известна дифференциальная функция, можно найти интегральную функцию распределения:
. Если известна дифференциальная функция, можно найти интегральную функцию распределения: 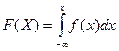 .
.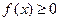 .
.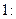
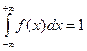 .
.


