
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные и дифференциалы высших порядковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция f(x) определена и дифференцируема на некотором промежутке X, тогда ее производная f'(x) также является функцией от x на этом промежутке. Если f '(x) имеет производную на промежутке X, то эта производная называется производной второго порядка функции y = f(x) и обозначается: y'' или f''(x). Итак, f''(x) = (f '(x))'. Производная от производной второго порядка называется производной третьего порядка и обозначается: y''' или f '''(x). Вообще, производной n-го порядка называется производная от производной (n – 1)-го порядка и обозначается: y(n) или f (n)(x). Итак, f(n)(x) = (f (n-1)(x))'. Производные y'', y''',... называются производными высших порядков. Пример 1. Решение. Пример 2. Найти производную n-го порядка для функции y = e3x. Решение. y' = 3e3x, y'' = 3× 3e3x = 32e3x, y''' = 33e3x. По аналогии находим: y(n) = 3ne3x. Рассмотрим механический смысл второй производной. Пусть путь S, пройденный телом по прямой за время t, выражается формулой S = f(t). Известно, что при этом скорость V в момент времени t равна производной от пути по времени: V =S '(t). В момент времени t + Δt скорость получит приращение ΔV = V(t + Δt) – V(t). Отношение
Следовательно, ускорение при прямолинейном движении равно второй производной от пути по времени: a = S''(t). Перейдем к рассмотрению дифференциалов высших порядков. Пусть y = f(x), x Дифференциал от дифференциала функции называется д ифференциалом второго порядка и обозначается d2y или d2f(x). Итак, d2y = d(dy), но dy= dx, поэтому d2y = d(f '(x) dx) = (f''(x) dx)dx = f''(x)(dx)2. Будем вместо (dx)2 писать dx2. Дифференциалом третьего порядка называется дифференциал от дифференциала второго порядка и обозначается d3y или d3f(x): d3y = d(d2y) = d(f''(x) dx2) = f'''(x)dx3 и т.д. Дифференциалом n-го порядка называется дифференциал от дифференциала Итак, dny = f (n)(x)dxn. Отсюда Заметим, что выражение производной через отношение дифференциалов часто бывает удобно, поэтому оно широко используется. Так, вместо y'x будем писать: Пример 3. Найти d3y для функции y = cos2x. y' = (cos2x)' = –2cosxsinx = –sin2x, y'' = (–sin2x)' = –2cos2x, y''' = 4sin2x. Следовательно, d3y = 4sin2xdx3. Рассмотрим нахождение производных высших порядков для функций, заданных параметрически и неявно. Пусть функция y, зависящая от x, задана параметрически уравнениями Пример 4. Функция y от x задана параметрически уравнениями:
Нахождение производных высших порядков от функций, заданных неявно, рассмотрим на примере. Пример 5. Найти
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.124 (0.009 с.) |

 . Найти f ''(x) и f ''(4).
. Найти f ''(x) и f ''(4).
 называется средним ускорением за время Δt. Ускорением a в данный момент времени называется предел среднего ускорения, когда Δt → 0:
называется средним ускорением за время Δt. Ускорением a в данный момент времени называется предел среднего ускорения, когда Δt → 0:
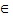 X. Дифференциал этой функции y = f'(x)dx является функцией от x (если x – не фиксированное число), dx – приращение аргумента x, оно не зависит от x.
X. Дифференциал этой функции y = f'(x)dx является функцией от x (если x – не фиксированное число), dx – приращение аргумента x, оно не зависит от x. .
. , вместо y't пишем:
, вместо y't пишем:  .
. (T – некоторый промежуток).
(T – некоторый промежуток).  (разд.2.6), поэтому
(разд.2.6), поэтому  .
.  и т.д.
и т.д.
 .
. 
 , для функции, заданной неявно уравнением:
, для функции, заданной неявно уравнением: 

 . Подставим x = 0 в исходное уравнение ey + xy = e, получим: ey + 0×y = e, откуда y = 1, значит,
. Подставим x = 0 в исходное уравнение ey + xy = e, получим: ey + 0×y = e, откуда y = 1, значит, 



