
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы о дифференцируемых функциях.
Теорема Ферма. Пусть функция f(x) определена, непрерывна на интервале (a, b) и в некоторой точке x0 этого интервала принимает свое наибольшее или наименьшее значение. Если в точке x0 существует производная этой функции, то f' (x0)= 0. Доказательство. Пусть f(x0) = M – наибольшее значение функции на (a, b). Покажем, что f'(x0) = 0. По определению производной
Если Δx < 0, то
Теорема Ролля. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в каждой внутренней точке и f(a) = f(b), то существует, по крайней мере, одна внутренняя точка x0 отрезка [a, b], что f'(x0) = 0. Доказательство. Так как функция непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и своего наименьшего значения m (см. главу 1) Если M = m, то функция f(x) постоянна на отрезке [a, b], а потому f'(x) = 0 для любого x Теорема Коши. Пусть функции f(x), g(x) непрерывны на отрезке [a, b], дифференцируемы на (a, b), причем g'(x) ¹ 0 для любой точки x из интервала (a, b). Тогда существует внутренняя точка x0 отрезка [a, b], такая, что
Теорема Лопиталя. (Раскрытие неопределенностей типа Пусть функции f(x), g(x) определены, непрерывны и дифференцируемы в точке x0 и некоторой ее окрестности, причем g'(x) ≠0 для любого x из этой окрестности, и пусть f(x0) = 0, g(x0) = 0 (следовательно, f(x), g(x) – бесконечно малые при x→x0). Если
Пример 1. Найти
Теорема Лопиталя. (Раскрытие неопределенностей типа Пусть функции f(x), g(x) дифференцируемы в окрестности точке x0, за исключением самой точки x0, причем g'(x)≠ 0, и пусть Рассмотрим неопределенности других видов. Если
Аналогично понимаются и другие неопределенности. При раскрытии таких неопределенностей зачастую помогает способ сведения их к неопределенностям типа Пример 4. Найти
Формула Тейлора. Формула Тейлора является одной из важнейших формул математического анализа, она имеет очень большое число теоретических и практических применений. Рассмотрим предварительно следующую задачу: данный многочлен Pn(x) степени n разложить по степеням разности (x – x0) (где x0 – некоторое число), т.е. представить Pn(x) в виде: Pn(x) = a0+ a1(x – x0) + a2(x – x0)2+...+ an(x – x0)n. (2.19) Вычислим коэффициенты: a0, a1,..., an. Для этого найдем сначала производные от Pn(x): P'n(x) = a1+ 2a2(x – x0) + 3a3(x – x0)2 +... + n×an(x – x0)n–1; Полагая в равенствах (2.19), (2.20) x = x0, получим: Pn(x0) = a0, (x0) = a1, (x0) = 2a2, Pn(n)(x0) = 2×3a3,..., Pn(n)(x0) = 1×2×...(n – 1)×n×an, Пусть функция f(x) имеет производные до (n + 1)-го порядка включительно в некотором промежутке, и число x0 принадлежит этому промежутку. Поставим задачу: найти многочлен n-й степени Pn(x), такой, чтобы значение Pn(x0) совпадало с f(x0), а значение всех производных для Pn(x) в точке x0 (до n-го порядка) совпадало со значениями соответствующих производных для f(x) в точке x0, т.е. Тогда по формуле (3) многочлен Pn(x) имеет вид: Естественно ожидать, что многочлен Pn(x) будет в некотором смысле «близок» к функции f(x), по крайней мере, около точки x0. Если для некоторого x остаточный член Rn(x) достаточно мал, то формула (2.23) дает приближенное значение для f(x): f(x)» Pn(x), при этом погрешность этого приближения равна: Rn(x). Для оценки Rn(x) применяются специальные формулы, одна из них называется формой Лагранжа и имеет вид: где c – некоторое число, заключенное между x0 и x. Число c можно представить в виде: Вообще говоря, значения θ в формулах (2.25) и (2.26) различные. Заметим, что если в формулах Тейлора (2.23) положить n = 0 и остаточный член записать в форме Лагранжа (2.24), то получим формулу: f(x) = f(x0) + f '(c)(x – x0), откуда приходим к формуле Лагранжа: f(x) – f(x0) = f '(c)(x – x0). Таким образом, формула Тейлора является обобщением формулы Лагранжа (конечных приращений). Если в формуле Тейлора (2.23) положить x0 = 0, то получится формула, называемая формулой Маклорена: где Рассмотрим применение формулы Тейлора. Найдем разложение некоторых элементарных функций по формуле Тейлора, причем возьмем x0 = 0 (т.е. найдем формулы Маклорена для этих функций).
1) f(x) = ex Так как f '(x) = ex, f '' (x) = ex,..., f (n)(x) = ex и f(0) = 1, f '(0) = 1, f ''(0) =1,..., Пример 1. Вычислить приближенно число e и оценить погрешность. Решение. Ранее нами было введено число e как предел последовательности: 2) f (x) = sinx Найдем производные до (n + 1)-го порядка для f(x) = sinx и их значения при x= 0:
Пример 2. Вычислить приближенно sin200 с точностью до 0,0001. Решение. Воспользуемся формулой (2.29), положив Вывести формулу Маклорена для функции f (x) = cosx (формулу (2.30)).
|
|||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 772; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.200.136 (0.018 с.) |
 .
. 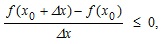 , а поэтому f '(x0)≤ 0.
, а поэтому f '(x0)≤ 0. , поэтому f '(x0)≥0. Так как f '(x0) – определенное число, то получаем, что f '(x0) = 0. Теорема доказана.
, поэтому f '(x0)≥0. Так как f '(x0) – определенное число, то получаем, что f '(x0) = 0. Теорема доказана.
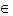 (a, b).
(a, b). 
 .
.  )
) существует, то существует
существует, то существует  (2.18)
(2.18)
 .
. 
 . В самом деле, если доопределить f (x), g(x), положив f(x0) = g(x0) = 0, тогда f(x), g(x) будут непрерывны в точке x0, а потому теорема Лопиталя будет применима к ним.
. В самом деле, если доопределить f (x), g(x), положив f(x0) = g(x0) = 0, тогда f(x), g(x) будут непрерывны в точке x0, а потому теорема Лопиталя будет применима к ним.  .
.  .
. )
) . Если существует
. Если существует 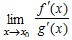 , то существует
, то существует  .
.  – не существует, так как
– не существует, так как  не существует.
не существует.  при x →x0 (x → ∞) является неопределенностью типа
при x →x0 (x → ∞) является неопределенностью типа  , и f '(x), g'(x) удовлетворяют условиям теоремы Лопиталя, то
, и f '(x), g'(x) удовлетворяют условиям теоремы Лопиталя, то 
 .
.  , следовательно, имеем отношение двух бесконечно больших при x → 0 и неопределенность типа
, следовательно, имеем отношение двух бесконечно больших при x → 0 и неопределенность типа  .
.  .
.  .
.  .
.  . Это означает, что показательная функция ex растет быстрее любой степенной функции xn.
. Это означает, что показательная функция ex растет быстрее любой степенной функции xn. называют неопределенностью типа 0×∞, а
называют неопределенностью типа 0×∞, а  – неопределенностью типа ∞0.
– неопределенностью типа ∞0. 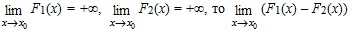 – неопределенность типа ∞ – ∞.
– неопределенность типа ∞ – ∞.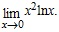 .
.  , то имеем неопределенность типа 0×∞. Преобразуем ее к виду:
, то имеем неопределенность типа 0×∞. Преобразуем ее к виду:  , затем применим правило Лопиталя,
, затем применим правило Лопиталя, 
 .
. 

 которая называется формулой Тейлора для функции f(x), а Rn(x) называется остаточным членом.
которая называется формулой Тейлора для функции f(x), а Rn(x) называется остаточным членом.



 – остаточный член в форме Лагранжа (0
– остаточный член в форме Лагранжа (0
 .
. и установлено, что 2 < e < 3. Используя формулу (2.28), положив x = 1,
и установлено, что 2 < e < 3. Используя формулу (2.28), положив x = 1,  , причем погрешность R8(1) не превосходит 0,00001.
, причем погрешность R8(1) не превосходит 0,00001.


 и потому Rn(x) по абсолютной величине не превосходит
и потому Rn(x) по абсолютной величине не превосходит 
 радиан и взяв 2 члена разложения:
радиан и взяв 2 члена разложения: 



