
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость, вогнутость графика и точки перегиба. ⇐ ПредыдущаяСтр 10 из 10
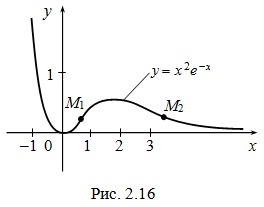
Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x). Теорема 1. (Достаточные условия выпуклости и вогнутости графика функции). Теорема 2 (достаточное условие точки перегиба) Пример. Исследовать на выпуклость, вогнутость и точки перегиба график функции y = x2e–x (см. разд. 2.13). Решение
При исследовании функции часто приходится устанавливать вид ее графика (а, значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой. Асимптотой графика функции y = f(x) называется такая прямая, что расстояние от переменной точки M на графике до этой прямой стремится к нулю при удалении точки M в бесконечность (рис. 2.17, 2.18).
С примерами асимптот мы встречались при изучении пределов функции (глава 1). Напомним, что если Пример 1. Найти вертикальные асимптоты для графика функции Решение. Функция Итак, если прямая y = kx + b является асимптотой графика функции y = f (x), то выполняется равенство (2.31) и наоборот, если при постоянных числах k, b выполняется равенство (2.31), то прямая y = kx + b является асимптотой. Из равенства (2.31), разделив бесконечно малую функцию (f(x) – kx – b) на x (а x → +∞), получим:
Аналогично решается вопрос об асимптотах при x → -∞. Заметим, что отдельно находить горизонтальные асимптоты нет надобности, они будут найдены при нахождении наклонных асимптот (при k = 0). Пример 2. Найти асимптоты линии y = ex – x. Решение. Функция f (x) = ex – x определена, непрерывна на бесконечном интервале (–∞, +∞), поэтому вертикальных асимптот нет. Найдем наклонные асимптоты, для этого вычислим пределы (2.33), (2.34) при x →+∞, x → -∞:
ГЛОССАРИЙ ВЫСКАЗЫВАНИЕ — понимается предложение, которое либо только истинно, либо только ложно ПРЕДИКАТ — это предложение с одной переменной или несколькими переменными. КОНЪЮНКЦИЯ — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложное выражение ложно. ДИЗЪЮНКЦИЯ — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны ИНВЕРСИЯ — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. ИМПЛИКАЦИЯ — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. ФУНКЦИЯ — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества. СЛОЖНАЯ ФУНКЦИЯ ИЛИ ФУНКЦИЯ ОТ ФУНКЦИИ — Если переменная y является функцией от x, y = f(x); а x – функция от переменной t: x = φ(t), то y = f(φ(t)) является функцией от t ПРОИЗВО́ДНАЯ (ФУНКЦИИ В ТОЧКЕ) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. ДИФФЕРЕНЦИАЛ ФУНКЦИИ В НЕКОТОРОЙ ТОЧКЕ Х — это главная, линейная часть приращения функции. Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента). Геометрический смысл дифференциала.
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.31 (0.01 с.) |
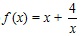 .
. 
 , то прямая y = b является асимптотой графика y = f(x) (при x → +∞), эта асимптота параллельна оси Ox и называется горизонтальной асимптотой (см. рис. 2.18). Аналогично, прямая y = b является асимптотой графика y = f(x) при x → -∞, если
, то прямая y = b является асимптотой графика y = f(x) (при x → +∞), эта асимптота параллельна оси Ox и называется горизонтальной асимптотой (см. рис. 2.18). Аналогично, прямая y = b является асимптотой графика y = f(x) при x → -∞, если  (рис. 2.17).
(рис. 2.17). 
 , тогда из определения асимптоты следует, что прямая x = x0 - асимптота. Очевидно и обратное, если прямая x = x0 является асимптотой, то хотя бы один из пределов,
, тогда из определения асимптоты следует, что прямая x = x0 - асимптота. Очевидно и обратное, если прямая x = x0 является асимптотой, то хотя бы один из пределов,  , является бесконечным (см. рис. 2.19, 2.20).
, является бесконечным (см. рис. 2.19, 2.20). 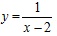 .
.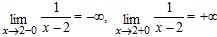 . Следовательно, прямая x = 2 является вертикальной асимптотой для графика
. Следовательно, прямая x = 2 является вертикальной асимптотой для графика 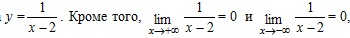 , следовательно, прямая y = 0 является горизонтальной асимптотой при x → +∞ и при x → -∞ (см. рис. 2.21).
, следовательно, прямая y = 0 является горизонтальной асимптотой при x → +∞ и при x → -∞ (см. рис. 2.21). 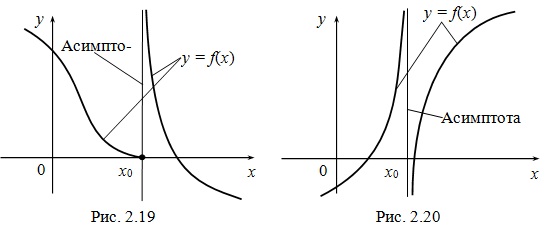
 . Из ΔMNK имеем
. Из ΔMNK имеем  , где a – угол наклона асимптоты к оси Ox, поэтому cosa –постоянная величина. Значит,
, где a – угол наклона асимптоты к оси Ox, поэтому cosa –постоянная величина. Значит,  Так как MK = |AK – AM|, AK = kx + b, то MK = |kx + b – f(x)|, следовательно,
Так как MK = |AK – AM|, AK = kx + b, то MK = |kx + b – f(x)|, следовательно, 




 так как
так как  (проверьте это по правилу Лопиталя). Отсюда следует, что при x →+∞ наклонных асимптот нет:
(проверьте это по правилу Лопиталя). Отсюда следует, что при x →+∞ наклонных асимптот нет: 
 , значит, b = 0.
, значит, b = 0. 


