
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логическая и математическая символикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
О КУРСЕ Дисциплина «Математический анализ» относится к базовой части математического и естественнонаучного цикла ООП бакалавриата и направлена на получение студентами прочных теоретических знаний и твердых практических навыков в области математической подготовки будущих бакалавров. Такая подготовка необходима для успешного усвоения многих специальных дисциплин, читаемых для бакалавров по направлению подготовки «Экономика». Дисциплина является одной из важнейших теоретических и прикладных математических дисциплин, определяющих уровень профессиональной подготовки современного бакалавра в области управления различными социально-экономическими процессами. Прочное усвоение современных математических методов позволит будущему специалисту в области экономики, бухгалтерского учета, банковского дела, налогов и налогообложения решать в своей повседневной деятельности актуальные практические задачи, понимать написанные на современном научном уровне результаты других исследований и тем самым совершенствовать свои профессиональные навыки. ЦЕЛЬ: Целью изучения дисциплины «Математический анализ» является формирование научного мировоззрения у студентов, формирование математических знаний, умений и навыков, необходимых для изучения других общенаучных и специальных дисциплин, самостоятельного изучения специальной литературы, математического исследования прикладных вопросов, правильного истолкования и оценки получаемых результатов, а также формирование навыков самостоятельной работы. Основной задачей изучения данной дисциплины является прочное усвоение студентами теоретических основ математического анализа, обучение использованию методов этой дисциплины в экономических исследованиях. Задачи дисциплины: понимание математики как особого способа познания мира, общности ее понятий и представлений;
ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ: В результате изучения дисциплины студент должен: Знать: основы математического анализа, необходимые для решения экономических задач.
МНОЖЕСТВА Понятие множества является первоначальным понятием математики, точное определение ему не дается, но его можно пояснить, описать через другие понятия. Можно сказать, что множество – это совокупность, собрание каких-то объектов, предметов, при этом объект, входящий в это множество, называют его элементом. Множества могут содержать как конечное число элементов, так и бесконечно много элементов. Рассматривают и множество, не содержащее элементов, его называют пустым и обозначают символом Ø. В математическом анализе чаще всего рассматриваются числовые множества, за некоторыми из них закреплены специальные обозначения. Так, множество всех натуральных чисел обозначаются через N и записывают так: N = {1,2,3,...}. Далее, через Z обозначают множество всех целых чисел, содержащее как натуральные числа, так и 0, и целые отрицательные числа; Z = {..., –3, –2, –1, 0, 1, 2, 3,...}. Рациональным называется число, которое можно представить в виде отношения двух целых чисел:
Известно, что любое рациональное число можно представить десятичной дробью, конечной и бесконечной периодической. Например, рациональное число 5/6 представимо бесконечной периодической дробью 5/6 = 0,83333..., а число 3/8 = 0,375. В последнем случае можно считать десятичную дробь тоже бесконечной с числом 0 в периоде: 3/8 = 0,3750000.... Известно, что всякую периодическую бесконечную дробь можно обратить в обыкновенную дробь p/q. Иррациональным числом называется всякая бесконечная непериодическая десятичная дробь. Множество всех рациональных и иррациональных чисел называется множеством действительных чисел и обозначается через R. Иными словами, множество действительных чисел R – это множество всех бесконечных десятичных дробей. Пусть M1, M2 – некоторые множества. Если каждый элемент множества M1 является элементом множества M2, то говорят, что M1 есть подмножество множества M2 и обозначается M1 Из определения числовых множеств можно заключить, что N Часто рассматриваются подмножества действительных чисел (a, b), [a, b], [a, b), (a, b] называемые, соответственно, интервалом, отрезком, полуинтервалом. Дадим символические определения этих множеств, а слово «называется» заменим на знак:
Заметим, что на числовой оси каждое действительное число изображается определенной точкой и любая точка числовой оси задает некоторое число, поэтому [a, b] изображается множеством всех точек отрезка, вместе с концами a, b, в то время как (a, b) – множеством точек отрезка без концов a, b.
Иногда рассматривается операция разности множеств A и B, это множество элементов A, не входящие в B. Обозначение: A\B. Таким образом,
ФУНКЦИИ Пусть x, y – переменные величины. Если каждому значению переменных x из множества A соответствует по определенному закону единственное значение переменной y, то говорят, что y является функцией (однозначной) от x и пишут y = f(x) или y = y(x). При этом переменную x называют аргументом или независимой переменной, множество A – областью определения функции y = f(x). Обозначим множество всех значений функции, т.е. {f(x)|x Пример 1. Для функции Пример 2. Замечание. Иногда рассматривают многозначные функции, допуская, что каждому значению x Следующие функции называются основными элементарными: 1) степенная функция Если y=f(x), z=g(y) - функции, то z=g(f(x)) сложная функция называется суперпозицией функций f и g. Элементарной называется всякая функция, которая может быть получена из конечного числа основных элементарных функций с помощью арифметических операций и операции суперпозиции. Например, элементарной является функция
Аналитический способ: связь между аргументом x и функцией y задается формулой, при этом на разных участках области определения она может задаваться различными формулами (см. пример 2). В примерах 1, 2 функции заданы аналитически. Табличный способ: функция задается таблицей отдельных значений аргумента и соответствующих значений функции. Такими являются таблицы тригонометрических функций, таблицы логарифмов и т.д. Графический способ: в этом случае соответствие между значениями x и y задается с помощью графика. Среди числовых функций особое место занимают функции с областью определения A = N. Пусть аргумент функции f(x) принимает только значения 1, 2, 3,....n,... Рассмотрим свойства, которыми могут обладать (или не обладать) некоторые функции. Функция f(x) называется возрастающей на множестве M (строго), если большему значению аргумента соответствует большее значение функции. Символически это может быть записано так: Функция f(x) называется убывающей (строго) на множестве M, если большему значению аргумента соответствует меньшее значение функции. Символически: Функция, убывающая или возрастающая на множестве M, называется монотонной на множестве M. Функция f(x) называется ограниченной сверху на множестве M, если существует такое число k, что для любого значения x Символически это может быть записано так: Аналогично дается определение функции, ограниченной снизу. Если функция ограничена и сверху, и снизу, то она называется ограниченной. Так, функция Функция f(x) называется четной, если Известно, что все тригонометрические функции являются периодическими. Введем важные понятия сложной и обратной функции. Если переменная y является функцией от x, y = f(x); а x – функция от переменной t: x = φ(t), то y = f(φ(t)) является функцией от t и называется сложной функцией или функцией от функции. Например, пусть y = x2, x = sint, тогда функция y = (sint)2 является сложной.
Пусть y = f(x) с областью определения A и множеством значений B такова, что для любого значения y Например, для функции y = x2 с областью определения [0, +∞) и таким же множеством значений обратной является функция:
ПРЕДЕЛЫ Предел последовательности Как отмечалось раньше, любая последовательность a1, a2,..., an,... есть функция натурального аргумента, an = f(n), n Число b называется пределом последовательности {an}, если для любого ε > 0 существует такое натуральное число n0, что для всех натуральных n, больших n0, выполняется неравенство: | an – b | < e. Обозначение:
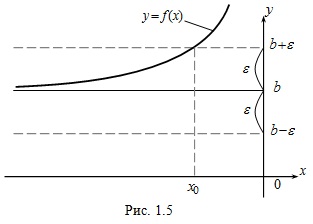
Предел функции при x→ –∞ Пусть функция y = f(x) определена на R или (–∞, a). Число b называется пределом функции f(x) при стремлении x к –∞ (x → –∞), если для любого положительного числа ε существует такое x0, что для всех x, меньших x0, выполняется неравенство: Геометрически этот факт означает, что точки графика y = f(x) (рис. 1.5) приближаются как угодно близко к соответствующим точкам прямой y = b при движении x влево неограниченно и что по фиксированному ε > 0 найдется число x0, такое, что для всех x, меньших x0, график y = f(x) заключен внутри полосы, ограниченной прямыми: y = b + ε, y = b – ε. Доказать самостоятельно, что Рассмотренные пределы объединяются общим названием «пределы на бесконечности». Не надо думать, что любая функция, определенная на R, имеет предел при x → +∞ или x → –∞. Например, sinx не существует, так как значения
Предел функции в точке Пусть функция f(x) определена в некоторой окрестности точки x0 (возможно, определена на R), но в самой точке x0 функция f(x) может быть и не определена. Дадим сначала описательное определение предела функции в точке и приведем пример. Число b называется пределом функции f(x) в точке x0 (x → x0), если значения f(x) приближаются к числу b как угодно близко при условии, что значения аргумента x подходят к x0 достаточно близко. Обозначение:
Пример 1. Функция
График функции:
Покажем, что Потребуем, чтобы Аналогично можно показать, что Дадим строгое определение предела функции в точке. Число b называется пределом функции f(x) в точке x0 (при стремлении x к x0), если для любого положительного числа e найдется положительное число δ, такое, что для любого x ≠ x0 и удовлетворяющему неравенству: x0 – δ < x < x0 + δ, выполняется неравенство: | f(x) – b| < ε. Символически Заметим, что условие: «x ≠ x0 и x0 – δ < x < x0 + δ» можно записать в виде неравенства: 0 < | x – x0 | Если Пример 2. Показать, что Основные теоремы о пределах Теорема 1. Если Теорема 2. Если функцию f(x) можно представить в виде: f (x) = b + a(x), где b – число, a(x) – б.м. функция при x → a, то Теорема 3. Предел суммы (разности) двух функций равен сумме (разности) их пределов, т.е. если Теорема 4. Предел произведения двух функций равен произведению их пределов, т.е. если Следствие 2. Если n – натуральное число, то Теорема 5. Предел дроби равен пределу числителя, деленному на предел знаменателя при условии, что предел знаменателя не равен нулю. Иначе, если
Пример. Найти Теорема 6. Если Теорема 8. (теорема о сжатой переменной). Если
Первый замечательный предел Рассмотрим функцию Второй замечательный предел Рассмотрим возрастающую последовательность: a1,a2,...,an,... Для нее an+1>an для любого натурального n. Если эта последовательность не является ограниченной, то она не имеет предела, так как ее члены неограниченно возрастают. Если же возрастающая последовательность ограничена, то она имеет предел. Этот факт доказывается в полных курсах математического анализа [6], мы приведем лишь его полную формулировку. НЕПРЕРЫВНОСТЬ ФУНКЦИИ Пусть функция f(x) определена в точке x0 и некоторой ее окрестности. Если существует На языке логики равенство Используя понятия односторонних пределов, можно перефразировать определение так: функция называется непрерывной в точке x0, если она определена в точке x0 и некоторой ее окрестности, если существуют Если Аналогично определяется непрерывность справа. Пример 1. Функция f(x) = x3 определена на R. Покажем, что f(x) непрерывна в точке x0 = 2. Пример 2. Покажем, что f(x) непрерывна в точке x0 = 0:
Дадим определение точек разрыва. Пусть f(x) определена в окрестности точки x0, но может быть не определена в x0.
Точка x0 разрыва первого рода, для которой 3. Если рассмотреть функцию Рассмотрим операции над непрерывными функциями. Теорема 1. Если функции f1(x) и f2(x) непрерывны в точке x0, то их сумма и произведение также непрерывны в точке x0. Если, кроме того, f2(x0) ≠0, то частное также непрерывно в точке x0. Установим непрерывность некоторых элементарных функций: 1. Всякая постоянная функция y = C непрерывна в каждой точке x0 2. Функция y = x непрерывна в любой точке x0, так как 3. Любой многочлен: y = a0 + a1x + a2x2 +...+ anxn, непрерывен в каждой точке числовой оси, как сумма непрерывных функций. 4. Всякая рациональная дробь, являющаяся отношением двух многочленов 5. Функция y = sinx, y = cosx непрерывны в точке x0 = 0, так как Теорема 3. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Если функция f(x) непрерывна в каждой точке интервала (a, b), то говорят, что f(x) непрерывна на интервале (a, b). Пример 6. Функция
ПРОИЗВОДНАЯ ФУНКЦИИ Решение
Переформулируем это определение, используя понятия приращения аргумента и приращения функции. Из этого равенства получаем:
Теорема. Если функция f(x) дифференцируема в точке x0, то она непрерывна в этой точке. Замечание. Если в точке x0 функция f (x) непрерывна, то в этой точке функция может и не иметь производной, что подтверждается следующим примером. Пример 2. Функция f(x) = | x | непрерывна в точке x0 = 0, так как Рассмотрим геометрический смысл производной.
На рис. 2.1 изображен график непрерывной функции y = f (x). Точка M0 на графике имеет координаты x0, f(x0), другая точка графика M – координаты x0 + Δx, f(x0 + Δx). Прямая M0M является секущей для линии y = f(x), она наклонена к оси Ox под углом β. Пусть f '(x0) существует, т.е. Таким образом, Итак, угловой коэффициент касательной к графику y = f (x) в точке с абсциссой x0 равен производной функции f(x) в точке x0: f '(x0) = k = tgα. В этом состоит геометрическое истолкование производной. Очевидно, что уравнение касательной M0K имеет вид: y – f (x0) = f '(x0)(x – x0). Переходим к рассмотрению механического смысла производной.
Пусть материальная точка движется прямолинейно неравномерно по закону S = f(t), где t – время, S – путь, проходимый точкой за время t. Пусть в момент времени t0 точка находилась в положении M0 (рис. 2.2). Поставим задачу: определить скорость материальной точки в момент t0. Рассмотрим другой момент времени t0 + Δt. За время t0 пройденный точкой путь равен: S0 = f (t0), за (t0 + Δt) пройдено расстояние S = f(t0 + Δt), и точка оказалась в положении M, тогда за время Δt пройден путь M0M и он равен: Средняя скорость Vср за пpомежуток времени Δt равна: Вывод. Производная от пути S = f(t) в момент времени t0 есть скорость в момент времени t0.
ДИФФЕРЕНЦИАЛ ФУНКЦИИ Пусть функция в точке x0 имеет производную. По определению: Δy = f '(x0)Δx + α×Δx. (2.7) При Δx → 0 второе слагаемое в равенстве (2.7) является бесконечно малой высшего порядка, по сравнению с Таким образом, приращение функции Δy состоит из двух слагаемых, из которых первое f '(x0)×Δx является главной частью приращения Δy, линейной относительно Δx (при f '(x0)≠ 0). Дифференциалом функции f(x) в точке x0 называется главная часть приращения функции и обозначается: dy или df (x0). Следовательно, df (x0) =f '(x0)×Δx. (2.8) Пример 1. Найти дифференциал функции dy и приращение функции Δy для функции y = x2 при: Решение 1) Δy = (x + Δx)2 – x2 = x2 + 2xΔx + (Δx)2 – x2 = 2xΔx + (Δx)2, dy = 2xΔx. 2) Если x0 = 20, Δx = 0,1, то Δy = 40×0,1 + (0,1)2 = 4,01; dy = 40×0,1= 4. Запишем равенство (2.7) в виде: Δy = dy + a×Δx. (2.9) Приращение Δy отличается от дифференциала dy на бесконечно малую высшего порядка, по сравнению с Δx, поэтому в приближенных вычислениях пользуются приближенным равенством Δy ≈ dy, если Δx достаточно мало. Учитывая, что Δy = f(x0 + Δx) – f(x0), получаем приближенную формулу: f(x0 + Δx) ≈ f(x0) + dy. (2.10) Пример 2. Вычислить приближенно Решение. Рассмотрим: Используя формулу (2.10), получим:
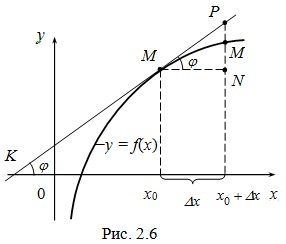
Значит, Рассмотрим геометрический смысл дифференциала df(x0) (рис. 2.6). Следовательно, дифференциал функции f(x) в точке x0 равен приращению ординаты касательной. Найдем дифференциал функции Если x – произвольное число, то из равенства (2.8) получаем df(x) = f '(x)dx, откуда Рассмотрим свойства дифференциала функции. Если u(x), v(x) – дифференцируемые функции, то справедливы следующие формулы:
Для доказательства этих формул используются формулы производных для суммы, произведения и частного функции. Докажем, например, формулу (2.12): d(u×v) = (u×v)'Δx = (u×v' + u'×v)Δx = u×v'Δx + u'Δx×v = u×dv + v×du. Рассмотрим дифференциал сложной ф
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.223 (0.017 с.) |

 . Множество всех рациональных чисел обозначается через Q. Символически определение множества рациональных чисел можно записать так:
. Множество всех рациональных чисел обозначается через Q. Символически определение множества рациональных чисел можно записать так:  . Здесь знак
. Здесь знак  заменяет слово «называется». Заметим, что множество можно задать перечислением элементов, а можно описанием свойств элементов (предикатом), как в последнем случае.
заменяет слово «называется». Заметим, что множество можно задать перечислением элементов, а можно описанием свойств элементов (предикатом), как в последнем случае. M2. Итак, M1
M2. Итак, M1 

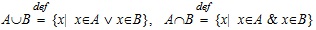
 . В частном случае R\Q есть множество иррациональных чисел.
. В частном случае R\Q есть множество иррациональных чисел.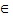 A}, через B.
A}, через B.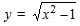 область определения A = (–∞, –1] U [1, +∞), множество значений B = [0, +∞).
область определения A = (–∞, –1] U [1, +∞), множество значений B = [0, +∞).


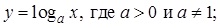

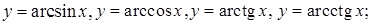
 В качестве примера неэлементарной функции укажем модуль действительного числа x
В качестве примера неэлементарной функции укажем модуль действительного числа x


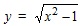 ограничена снизу на множестве A (пример 1), а функция из примера 2 ограничена сверху на множестве R.
ограничена снизу на множестве A (пример 1), а функция из примера 2 ограничена сверху на множестве R. и называется нечетной, если
и называется нечетной, если  Например, функция y = x2 является четной, а y = sinx – нечетной.
Например, функция y = x2 является четной, а y = sinx – нечетной. 



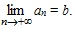 . Доказать самостоятельно, что
. Доказать самостоятельно, что 
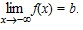 .
.
 при неограниченном возрастании x периодически меняются от –1 до +1, не приближаясь ни к какому постоянному числу. Аналогично, не существует
при неограниченном возрастании x периодически меняются от –1 до +1, не приближаясь ни к какому постоянному числу. Аналогично, не существует  . Последовательность: a1= 1, a2 = 3, a3= 5,..., an = 2n – 1,... также не имеет предела.
. Последовательность: a1= 1, a2 = 3, a3= 5,..., an = 2n – 1,... также не имеет предела. .
. определена во всех точках числовой оси, за исключением x0 = 2. Найдем
определена во всех точках числовой оси, за исключением x0 = 2. Найдем  , для этого вычислим значения f(x) для x, близких к 2, и построим график: y = f(x). Заметим, что для x ≠ 2:
, для этого вычислим значения f(x) для x, близких к 2, и построим график: y = f(x). Заметим, что для x ≠ 2:  .
.
 совпадает с прямой: y = 2x для всех x ≠ 2
совпадает с прямой: y = 2x для всех x ≠ 2 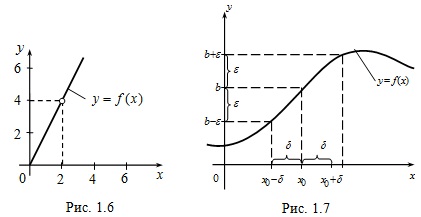
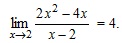 Для этого убедимся, что | f(x) – 4 | может стать настолько малым, насколько пожелаем:
Для этого убедимся, что | f(x) – 4 | может стать настолько малым, насколько пожелаем:  |, так как x ≠ 2.
|, так как x ≠ 2.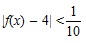 , тогда из неравенства:
, тогда из неравенства:  . Т.е. при значениях x, удовлетворяющих неравенству:
. Т.е. при значениях x, удовлетворяющих неравенству:  , выполняется неравенство
, выполняется неравенство  .
.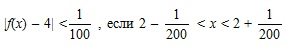 и, вообще, для любого (малого) положительного числа ε:
и, вообще, для любого (малого) положительного числа ε:  (или, что то же самое,
(или, что то же самое, 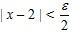 ). Обозначим
). Обозначим 
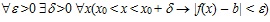
 x = x0.
x = x0.  , где a(x) – б.м. при x → a.
, где a(x) – б.м. при x → a. .
.
 .
. 
 .
.

 .
.  . Аналогично,
. Аналогично,  Используя теорему 5, получим:
Используя теорему 5, получим: 
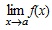 существует и f(x) ≥ 0 для всех x из области определения функции, то
существует и f(x) ≥ 0 для всех x из области определения функции, то 
 существуют, то
существуют, то 
 и
и 
 , аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция
, аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция  не определена.
не определена. 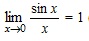 (первый замечательный предел).
(первый замечательный предел).  , то функция f(x) называется непрерывной в точке x0, а x0 называется точкой непрерывности функции f(x).
, то функция f(x) называется непрерывной в точке x0, а x0 называется точкой непрерывности функции f(x). описывается формулой:
описывается формулой: 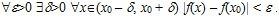
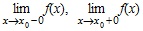 и
и 
 , значит, f(x) = x3 непрерывна в точке x0 = 2.
, значит, f(x) = x3 непрерывна в точке x0 = 2. .
.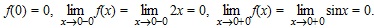
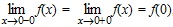 , то непрерывность функции f(x) в точке x0 = 0 доказана.
, то непрерывность функции f(x) в точке x0 = 0 доказана. .
. 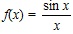 не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x).
не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x).  не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x).
не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x).  и т.д. График y = E(x) представлен на рис. 1.14.
и т.д. График y = E(x) представлен на рис. 1.14.
 .
.  то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.
то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.  . В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0 = 2 является точкой разрыва первого рода, так как
. В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0 = 2 является точкой разрыва первого рода, так как 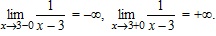 существуют пределы. В примере 4 x0 = 3 – точка разрыва второго рода, так как
существуют пределы. В примере 4 x0 = 3 – точка разрыва второго рода, так как  .
. , то φ(x) непрерывна в точке x0 = 0, так как
, то φ(x) непрерывна в точке x0 = 0, так как  . Доопределив функцию в точке x0 = 0, мы устранили разрыв.
. Доопределив функцию в точке x0 = 0, мы устранили разрыв. .
.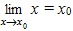 . Тогда функция y = Cxn, где n
. Тогда функция y = Cxn, где n  , непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.
, непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.
 непрерывна на интервалах (–∞, 3) и (3, +∞), так как при x0≠ 3:
непрерывна на интервалах (–∞, 3) и (3, +∞), так как при x0≠ 3:  .
.


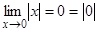 .
. 

 есть некоторое число. Из ΔM0MА получаем:
есть некоторое число. Из ΔM0MА получаем: 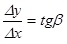 (известно, что tgβ – угловой коэффициент прямой M0M). Если Δx → 0, то точка M движется по графику функции y = f(x), приближаясь к точке M0, при этом секущая M0M, поворачиваясь вокруг точки M0, стремится занять предельное положение, т.е. совпасть с касательной M0K, при этом β→α (α – угол между касательной M0K и осью Ox), tgβ → tgα.
(известно, что tgβ – угловой коэффициент прямой M0M). Если Δx → 0, то точка M движется по графику функции y = f(x), приближаясь к точке M0, при этом секущая M0M, поворачиваясь вокруг точки M0, стремится занять предельное положение, т.е. совпасть с касательной M0K, при этом β→α (α – угол между касательной M0K и осью Ox), tgβ → tgα.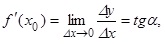 но tgα = k есть угловой коэффициент касательной M0K.
но tgα = k есть угловой коэффициент касательной M0K.
 . Но средняя скорость может быть различной, в зависимости от промежутка времени Δt. Скоростью в момент времени t0 (обозначим V(t0)) называется предел средней скорости Vср при Δt → 0. Итак,
. Но средняя скорость может быть различной, в зависимости от промежутка времени Δt. Скоростью в момент времени t0 (обозначим V(t0)) называется предел средней скорости Vср при Δt → 0. Итак, 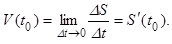
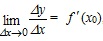
 , где a – бесконечно малая при Δx → 0. Отсюда
, где a – бесконечно малая при Δx → 0. Отсюда , поэтому Δy и f ' (x0)×Δx – эквивалентные, бесконечно малые (при f '(x0) ≠ 0).
, поэтому Δy и f ' (x0)×Δx – эквивалентные, бесконечно малые (при f '(x0) ≠ 0). .
.
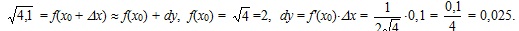 .
.
 .
. 



