
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пределы функции на бесконечности
Рассмотрим одно из центральных понятий математического анализа – понятие предела функции. Ввиду сложности для понимания этого понятия сначала дадим его описательное определение, подкрепленное примерами, а затем строгое определение. Предел функции при x → +∞ Пусть функция y = f(x) определена на множестве всех действительных чисел R или на бесконечном интервале (a, +∞). Обозначение: Пример 1. Функция
Из таблицы видно, что значения функции приближаются к числу 2 с увеличением x. Убедимся, что
Пусть ε – произвольное (малое) положительное число, тогда найдется такое x0, что f(x) – 2 x > x0. Действительно,
Из таблицы значений и графика (рис. 1.3) видим, что с ростом x значения f(x) приближаются к 1, оставаясь меньше 1. Покажем, что Покажем, что |f(x) – 1| может стать меньше любого заданного положительного числа ε при достаточно больших x. Для этого решим неравенство
Число b называется пределом функции f(x) при стремлении x к +∞, если для любого положительного числа e найдется такое число x0, что для всех x, больших x0, выполняется неравенство: f(x) – b |
Геометрическая интерпретация этого определения приведена на рис. 1.4. В логических символах это определение выглядит так:
Обозначим: Пусть для некоторой функции Из определения предела следует, что по произвольному ε > 0 найдется такое x0, что для всех x, больших x0, график y = f(x) заключен внутри полосы, ограниченной прямыми: y = b + ε, y = b – ε.
Предел последовательности Как отмечалось раньше, любая последовательность a1, a2,..., an,... есть функция натурального аргумента, an = f(n), n Число b называется пределом последовательности {an}, если для любого ε > 0 существует такое натуральное число n0, что для всех натуральных n, больших n0, выполняется неравенство: | an – b | < e. Обозначение:
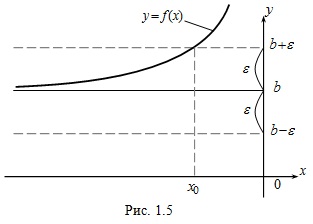
Предел функции при x→ –∞ Пусть функция y = f(x) определена на R или (–∞, a). Число b называется пределом функции f(x) при стремлении x к –∞ (x → –∞), если для любого положительного числа ε существует такое x0, что для всех x, меньших x0, выполняется неравенство: Геометрически этот факт означает, что точки графика y = f(x) (рис. 1.5) приближаются как угодно близко к соответствующим точкам прямой y = b при движении x влево неограниченно и что по фиксированному ε > 0 найдется число x0, такое, что для всех x, меньших x0, график y = f(x) заключен внутри полосы, ограниченной прямыми: y = b + ε, y = b – ε. Доказать самостоятельно, что Рассмотренные пределы объединяются общим названием «пределы на бесконечности». Не надо думать, что любая функция, определенная на R, имеет предел при x → +∞ или x → –∞. Например, sinx не существует, так как значения
Предел функции в точке Пусть функция f(x) определена в некоторой окрестности точки x0 (возможно, определена на R), но в самой точке x0 функция f(x) может быть и не определена. Дадим сначала описательное определение предела функции в точке и приведем пример. Число b называется пределом функции f(x) в точке x0 (x → x0), если значения f(x) приближаются к числу b как угодно близко при условии, что значения аргумента x подходят к x0 достаточно близко. Обозначение: Пример 1. Функция
График функции:
Покажем, что Потребуем, чтобы Аналогично можно показать, что Дадим строгое определение предела функции в точке. Число b называется пределом функции f(x) в точке x0 (при стремлении x к x0), если для любого положительного числа e найдется положительное число δ, такое, что для любого x ≠ x0 и удовлетворяющему неравенству: x0 – δ < x < x0 + δ, выполняется неравенство: | f(x) – b| < ε. Символически Заметим, что условие: «x ≠ x0 и x0 – δ < x < x0 + δ» можно записать в виде неравенства: 0 < | x – x0 | Если Пример 2. Показать, что
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.7 (0.014 с.) |
 .
. определена на интервале (0, +∞). Составим таблицу ее некоторых значений и построим ее график (рис. 1.2):
определена на интервале (0, +∞). Составим таблицу ее некоторых значений и построим ее график (рис. 1.2):
 .
. показывает, на сколько отличается f(x) от 2. Так, если x равно 10, то f(x) отличается от 2 на 1/10, а если x = 100, то f(x) – 2 = 1/100. Разность f(x) – 2 может стать меньше любого заданного положительного числа ε, если x взять достаточно большим. Например, ε = 1/1000. Чтобы определить, для каких значений x выполняется неравенство f(x) – 2 < 1/1000, надо решить это неравенство:
показывает, на сколько отличается f(x) от 2. Так, если x равно 10, то f(x) отличается от 2 на 1/10, а если x = 100, то f(x) – 2 = 1/100. Разность f(x) – 2 может стать меньше любого заданного положительного числа ε, если x взять достаточно большим. Например, ε = 1/1000. Чтобы определить, для каких значений x выполняется неравенство f(x) – 2 < 1/1000, надо решить это неравенство:  , отсюда x > 1000.
, отсюда x > 1000.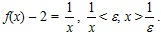 . Обозначив
. Обозначив  , получаем, что для всех x, если x > x0, то f(x) – 2 < ε. Итак мы показали, что
, получаем, что для всех x, если x > x0, то f(x) – 2 < ε. Итак мы показали, что  .
.  определена на (–2, +∞). Выпишем таблицу ее некоторых значений и построим график (рис. 1.3).
определена на (–2, +∞). Выпишем таблицу ее некоторых значений и построим график (рис. 1.3).
 . Разность f(x) – 1 отрицательна, поэтому вычислим ее абсолютную величину:
. Разность f(x) – 1 отрицательна, поэтому вычислим ее абсолютную величину: 
 , получим:
, получим:  Обозначим:
Обозначим:  . Таким образом, если x > x0, то | f(x) – 1| < ε. Например, возьмем в качестве ε число 0,01, тогда:
. Таким образом, если x > x0, то | f(x) – 1| < ε. Например, возьмем в качестве ε число 0,01, тогда:  Этим мы показали, что
Этим мы показали, что  (рис. 1.3).
(рис. 1.3).



 . Зафиксируем произвольное ε > 0, покажем, что найдется такое x0, что для всех x, больших x0: | f(x) – 0 | < e. Действительно,
. Зафиксируем произвольное ε > 0, покажем, что найдется такое x0, что для всех x, больших x0: | f(x) – 0 | < e. Действительно, 
 , тогда при x > x0: |f(x) – 0 | < ε, значит,
, тогда при x > x0: |f(x) – 0 | < ε, значит,  .
. , геометрически это означает, что точки графика y = f(x) приближаются к точкам прямой y = b (с той же абсциссой) при неограниченном возрастании x. В этом случае говорят, что прямая y = b является асимптотой графика y = f(x) при x→ +∞.Неравенство: | f(x) – b | b – ε < f(x) < b + ε.
, геометрически это означает, что точки графика y = f(x) приближаются к точкам прямой y = b (с той же абсциссой) при неограниченном возрастании x. В этом случае говорят, что прямая y = b является асимптотой графика y = f(x) при x→ +∞.Неравенство: | f(x) – b | b – ε < f(x) < b + ε.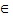 N. Определение предела последовательности почти дословно повторяет определение предела функции при x→+∞.
N. Определение предела последовательности почти дословно повторяет определение предела функции при x→+∞.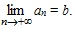 . Доказать самостоятельно, что
. Доказать самостоятельно, что 
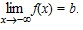 .
.
 при неограниченном возрастании x периодически меняются от –1 до +1, не приближаясь ни к какому постоянному числу. Аналогично, не существует
при неограниченном возрастании x периодически меняются от –1 до +1, не приближаясь ни к какому постоянному числу. Аналогично, не существует  . Последовательность: a1= 1, a2 = 3, a3= 5,..., an = 2n – 1,... также не имеет предела.
. Последовательность: a1= 1, a2 = 3, a3= 5,..., an = 2n – 1,... также не имеет предела. .
. определена во всех точках числовой оси, за исключением x0 = 2. Найдем
определена во всех точках числовой оси, за исключением x0 = 2. Найдем  , для этого вычислим значения f(x) для x, близких к 2, и построим график: y = f(x). Заметим, что для x ≠ 2:
, для этого вычислим значения f(x) для x, близких к 2, и построим график: y = f(x). Заметим, что для x ≠ 2:  .
.
 совпадает с прямой: y = 2x для всех x ≠ 2
совпадает с прямой: y = 2x для всех x ≠ 2 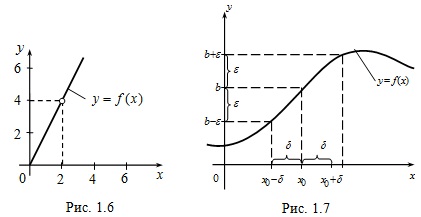
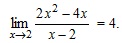 Для этого убедимся, что | f(x) – 4 | может стать настолько малым, насколько пожелаем:
Для этого убедимся, что | f(x) – 4 | может стать настолько малым, насколько пожелаем:  |, так как x ≠ 2.
|, так как x ≠ 2.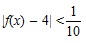 , тогда из неравенства:
, тогда из неравенства:  . Т.е. при значениях x, удовлетворяющих неравенству:
. Т.е. при значениях x, удовлетворяющих неравенству:  , выполняется неравенство
, выполняется неравенство  .
.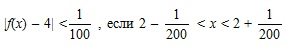 и, вообще, для любого (малого) положительного числа ε:
и, вообще, для любого (малого) положительного числа ε:  (или, что то же самое,
(или, что то же самое, 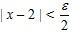 ). Обозначим
). Обозначим 
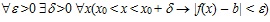
 x = x0.
x = x0. 


