Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
МатематическОЕ моделиРОВАНИЕСодержание книги
Поиск на нашем сайте
Министерство сельского хозяйства Российской Федерации Ижевская государственная сельскохозяйственная академия Кафедра “Эксплуатации МТП” Факультет непрерывного профессионального образования
МатематическОЕ моделиРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ на ЭВМ Методические материалы по изучению дисциплины и задания для контрольной работы
Ижевск 2011
Составитель канд. техн. наук, доцент кафедры ЭМТП Храмешин А.В. Математическое моделирование технологических процессов на ЭВМ: Методические указания по изучению дисциплины / ИжГСХА заочного и непрерывного профессионального образования. Предназначены для студентов специальностей:
“Механизация сельского хозяйства”, “Технология обслуживания и ремонта машин в АПК”, “Механизация переработки сельскохозяйственной продукции”, “Технология продуктов общественного питания”.
Утверждены методической комиссией Агроинженерного факультета. Данные методические указания являются дополнением к лекционному курсу, читаемому по дисциплине и являются руководством для самостоятельного изучения материала и выполнения контрольной работы в межсессионный период. Рецензенты: канд. экон. наук, доцент С.Н. Шмыков, канд. техн. наук, доцент С.П. Игнатьев
______________________ электроннный _________________ Заказ Тираж ИжГСХА 2011
Раздел 1 ОБЩИЕ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ ЦЕЛЬ И ЗАДАЧИ КУРСА
Курс “Математическое моделирование технологических процессов на ЭВМ” является завершением теоретической части базовой подготовки бакалавров и инженеров сельскохозяйственного профиля в ИжГСХА. Материал курса основан на знаниях, полученных студентами в результате изучения курсов “Вычислительная техника и программирование”, “Высшая математика”, общенаучных и общеинженерных дисциплин. Характерной чертой мышления бакалавров и инженеров является умение пользоваться математическими абстракциями для понимания явлений окружающего мира. Это делает понимание путей использования математического аппарата важным элементом общей культуры, а освоение математических моделей необходимой частью подготовки бакалавра и инженера в вузе. Целью дисциплины “Математическое моделирование технологических процессов на ЭВМ ” является обучение студентов общим вопросам теории моделирования, методам построения математических моделей и формального описания процессов и объектов, применению математических моделей для проведения вычислительных экспериментов и решения оптимизационных задач. В задачи курса входит ознакомление студентов: - с основными понятиями моделирования; - с теоретическими положениями и экспериментальными данными, используемыми для построения математических моделей в области профессиональной деятельности студентов; - с численными методами реализации моделей на ЭВМ; - с методами постановки и построения вычислительных экспериментов; - с выработкой умения использовать пакеты прикладных программ в профессиональной деятельности бакалавра и инженера сельско-хозяйственного профиля. Умение разрабатывать и использовать математические модели необходимо студентам при изучении специальных дисциплин, при выполнении курсовых и дипломных проектов, моделирования рабочих ситуаций, принятия оптимизационных организационно технологических и производственных решений.
Раздел 2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИЗУЧЕНИЮ СОДЕРЖАНИЯ ТЕМ И РАЗДЕЛОВ КУРСА ВВЕДЕНИЕ
Построение математической модели начинается с постановки задачи, то есть с выделения задачи, поддающейся математическому описанию и анализу. При этом необходимо выделить основные, существенные особенности объекта. При моделировании физических явлений этот процесс играет решающую роль, поскольку невозможно учесть в модели всё многообразие реального мира. Именно в результате такой идеализации возникли ткани без трения, невесомые нерастяжимые нити, идеальные газы и другие подобные понятия, широко используемые в физике и механике. Основные этапы математического моделирования: 1 этап - должны быть определены конечные цели при решении конкретной задачи; набор факторов и показателей, взаимосвязь между которыми интересует исследователя; роль факторов и показателей; входные и выходные параметры Входные - это параметры, с которыми оперирует исследователь при работе над составлением и проработкой математической модели. Выходные - это параметры, получаемые после реализации математической модели. 2 этап - математическая формализация. 3 этап - собственно моделирование - вывод общего вида модельных соотношений, связанных между собой входных и выходных параметры, в результате должны иметь аналитическую запись. 4 этап - оценивание параметров, входящих в аналитическую запись. 5 этап - сопоставление модельных заключений с реально наблюдаемой действительностью или анализ адекватности модели. 6 этап - зависит от результатов предыдущих этапов и заключается в планировании и проведении исследований, направленных на уточнение и улучшение модели. После построения модели необходимо убедиться в ее адекватности моделируемому объекту. Во-первых, модель должна быть непротиворечивой и подчиняться всем законам математической логики. Во-вторых, адекватность зависит от целей рассматриваемой задачи, например, от требуемой точности решения. Для численного моделирования на ЭВМ математическую модель необходимо перевести на язык “понятный” ЭВМ, то есть написать машинную программу. При моделировании на ЭВМ широко применяются пакеты прикладных программ. Пакетом прикладных программ называется программное средство, предназначенное для решения определенного круга задач. Основные области применения пакетов прикладных программ приведены в приложении A. Классификация основных областей применения отечественных и зарубежных пакетов прикладных программ приведена в приложении Б. После проведения расчетов работа с моделью не закончена. Необходимо совершить обратный переход с математического языка на тот язык, на котором первоначально формулировалась задача. Вопросы для самопроверки: 1. Перечислите основные этапы математического моделирования, раскройте их сущность? 2. Поясните этапы математического моделирования на конкретном примере? 3. Что называется пакетом прикладных программ? 4. Для чего предназначены пакеты прикладных программ?
ОБЩИЕ ВОПРОСЫ ТЕОРИИ МОДЕЛИРОВАНИЯ Методические рекомендации
В первом фрагменте курса студенты знакомятся с общими принципами моделирования. Моделирование — это замена объекта, подлежащего исследованию (оригинала), другим объектом (моделью), исследование модели и распространение результатов этого исследования на оригинал. Модель - это объект заменитель, который в определенных условиях может заменить объект оригинал, воспроизводя интересующие исследователя свойства и характеристики оригинала, причем объект заменитель имеет существенные преимущества и удобства: - наглядность (обозримость); - доступность испытаний; - легкость оперирования с ним. Моделирование объектов преследует различные цели. Главная из них - это предсказание новых результатов или поведения объекта в некоторых условиях. Предсказания могут относиться к условиям, которые по всей вероятности, будут иметь место в некоторый момент в будущем, а также к объектам, непосредственный эксперимент, которыми невозможен или дорог. Другой важной целью математического моделирования является углубление понимания объекта или явления. Именно эту роль и играют многие физические теории, хотя на их основе делаются также и прогнозы. Умение работать с математической моделью заключается в её анализе аналитическими и численными методами. Аналитические методы традиционны в математике. Их достоинством является наглядность результата. Обычно это формула для определения искомой величины. Аналитические решение существуют не для всех задач, а во многих случаях они слишком сложны. В таких случаях математические модели исследуют численными методами с помощью ЭВМ. Описание объекта с помощью математических выражений называется математической моделью. Классификация моделей: 1. Познавательные (теоретические) - являются формой организации и представлением знании, средством соединения новых знаний с уже имеющимися. 2. Прагматические (практические) - являются средством организации практических действий. 3. Статические (не изменяющиеся во времени) – например, план установки оборудования. 4. Динамические (изменяющиеся во времени) - процесс изменения состояния явления вещества, объекта. Например, три состояния вещества: пар, вода, лёд. Способы воплощения моделей. Для построения модели в распоряжении исследователя имеются: средства окружающего внешнего мира средства самого сознания. В зависимости от способа воплощения модели подразделяются на: абстрактные и материальные. Абстрактные модели - это идеальные конструкции, построенные средствами мышления (языковые конструкции). Особенности языковых конструкций: Достоинства: возможность иерархического построения модели по принципу “слово - предложение – текст”, что позволяет любую ситуацию промоделировать с достаточной для практических целей точностью, при этом важную роль имеют неязыковые формы мышления (интуиция, эмоции, озарение, подсознание). Недостатки: обладают многозначностью, многовариантностью и т. д. Материальные модели - это реальные конструкции, выполняющие определенные функции (вещественные конструкции), чтобы вещественная модель могла быть отображением оригинала. Между ними должны быть установлены отношения подобия, схожести. Способы установления подобия: - физическое (соответствие материалов); - геометрическое (отношение размеров модели кратны размерам объекта). Любые модели являются целевым отображением объекта. Особенности моделей: - целостность; - относительная обособленность от окружающей среды; - подчиненность определенной цели; - ингерентность (соответствие культурной среде); - адекватность (соответствие в мере, достаточной для достижения цели, требование полноты, точности и достоверности). Математическая модель - абстракция реального мира или объекта, в которой интересующие исследователя отношения между реальными явлениями заменены соответствующими отношениями между математическими объектами.
Способы определения математических моделей: 1. Аксиоматический - определяется непротиворечивым набором аксиом. 2. Конструктивный - определяется по реальным размерам предмета. Классификация математических моделей: - познавательные; - прагматические; - статические; - динамические; - квазистатические (t —> оо) По виду информации: - детерминированные; - непрерывные (дискретные); - фиксированные; - изменяющиеся. По форме представления: - инвариантные; - аналитические; - в виде схем, диаграмм, таблиц. Модели (математические) могут использоваться для проектирования (синтеза), анализа (исследования) и оценки функционирования систем (реальных объектов). В настоящее время моделирование используется для исследования разнообразных систем, в частности, городских, экономических, коммерческих, производственных, сельскохозяйственных, биологических, социальных, транспортных систем, систем здравоохранения и др. Вопросы для самопроверки 1. Что такое моделирование, модель объекта? 2. Что такое математическая модель? 3. Какие цели стоят перед моделированием? 4. Приведите примеры математических моделей. Для чего они используются? 5. Какими методами исследуются математические модели?
Электрических цепей В электротехнике часто встречается задача расчета линейных электрических цепей. Математической моделью таких цепей является система алгебраических уравнений, основанных на законах Кирхгофа. Для анализа математических моделей стационарных режимов электрических цепей широко применяются методы контурных токов и узловых потенциалов. Эти методы подробно изучаются в курсе “Теоретические основы электротехники”. В настоящем курсе остановимся на применении ЭВМ для расчетов электрических цепей. Они основаны на применении матричных методов. Топология электрической цепи описывается в виде топологических матриц, описывающих связи, например, между контурами. В итоге, модель сводится к системе линейных уравнений, в которой число уравнений равно числу неизвестных. Такую систему можно записать в матричном виде: AI=U, (1) где A=[a kj] — квадратная матрица коэффициентов при неизвестных токах. I = [i j] —вектор столбец неизвестных токов, U =[u к] —вектор столбец источников ЭДС ветвей. Вопросы для самопроверки 1. Что называется матрицей? 2. Какие виды матриц используются при проведении технических расчётов? 3. Какие варианты решений возникают при решении систем линейных уравнений? 4. Какую математическую форму имеет модель линейной электрической цепи? Вопросы для самопроверки 1. В чем состоит метод Гаусса решения системы линейных уравнений? 2. Какие преобразования выполняются при прямом ходе метода? 3. Какие преобразования выполняются при обратном ходе метода? 4. Какая система линейных алгебраических уравнений называется невырожденной? 5. В чем особенность метода Гаусса с выбором главного элемента? Вопросы для самопроверки 1. Какие динамические объекты относятся к линейным? 2. Какие динамические объекты относятся к стационарным? 3. Приведите математическую формулировку задачи Коши для линейного дифференциального уравнения первого порядка.? 4. Приведите примеры использования дифференциальных уравнений в профессиональной деятельности? Численные методы решения обыкновенных дифференциальных уравнений Лишь очень немногие дифференциальные уравнения могут быть решены точно, аналитическими методами, и поэтому обычно необходимо приближать решение численными методами. Пусть требуется найти приближенное решение дифференциального уравнения y¢ = ¦ (y, t), удовлетворяющее начальному условию y (t0) = y0. Численное решение задачи состоит в нахождении значений y1, y2, …yn функции (y(t) в точках t1, t2,...tn). Точки t1, t2,...tn называют узлами сетки, а расстояние между ними — шагом. Часто решение выполняют с постоянным шагом, тогда t1 = t0 + ih, (11) где i = 1, 2,... n, h — шаг сетки. Рассмотрим два метода. Одношаговым называется метод, в котором для расчетов следующей точки требуется информация только о последней вычислительной точке. Первый из рассматриваемых методов — метод Эйлера. В методе Эйлера каждое следующее значение функции вычисляется по предыдущему по формуле: yi+1 = yi + hצ(yi, ti), i = 1, 2,... n, (12) Фрагмент программы на языке Бейсик, реализующий метод Эйлера приведен в приложении Б. Другим распространенным одношаговым методом является метод Рунге-Кутта. В этом методе величину yi+1 вычисляют по следующим формулам: yi+1 = yi + hצ(yi, ti), i = 1, 2,... n,
где k1 = ¦(yi, ti); k2 = ¦(yi + k3 = ¦(yi + k4 = ¦(yi + h k3, ti + h);
Для оценки погрешности метода часто используют правило Рунге. Для этого проводят вычисления с шагом h и c шагом h/2. Если полученные значения отличаются в пределах допустимой погрешности, то шаг удваивают, в противном случае берут половинный шаг. Фрагмент программы на языке Бейсик, реализующий метод Рунге-Кутта, приведен в приложении Б.
Вопросы для самопроверки 1. Что называется сеткой и шагом метода? 2. Какие методы называются одношаговыми? 3. Приведите расчетную формулу метода Эйлера. Сколько вычислений приходится на одном шаге? 4. Приведите расчетные формулы метода Рунге-Кутта. Сколько вычислений производится на одном шаге? 5. Как оценить погрешность решения? Вопросы для самопроверки 1. Что называется имитационным экспериментом? 2. Что является предметом математической теории планирования эксперимента? 3. Что называется планом эксперимента? 4. Приведите примеры задачи оптимизации, укажите критерии оптимизации? Раздел 3. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ И УКАЗАНИЯ ПО ИХ ВЫПОЛНЕНИЮ
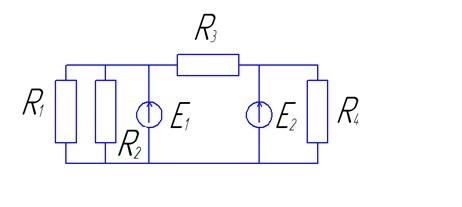
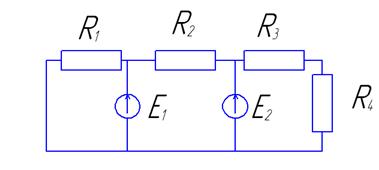
К выполнению контрольной работы следует приступать после изучения теоретического материала по соответствующему разделу, рассмотрев и усвоив вопросы курса. Для этого может быть применён вариант составления кроссворда, сканворда по пройденному материалу, которые представляются в контрольной работе как отчёт по теоретической части объёмом не менее 50 основных понятий. Решение задач контрольной работы должно сопровождаться краткими теоретическими пояснениями с приведением размерностей рассчитываемых величин. Блок-схемы алгоритмов должны вычерчиваться аккуратно с помощью чертежных принадлежностей. Перед проработкой программы следует привести таблицу соответствия обозначений физических величин в модели, именам переменных в программе. В конце работы следует расписаться, поставить дату, указать использованную литературу и время (в часах), затраченное на выполнение работы. Каждый студент получает индивидуальное задание, вариант задания выбирается по последней цифре шифра студенческого билета (или зачётной книжки). Первая задача выполняется по таблице 3, вариант схемы выбирается по таблице 2. Вторая задача выполняется по таблице 4, при этом студент самостоятельно предлагает вариант примера рассматриваемого динамического процесса, принимает числовые значения констант (от 1 до 9), комментирует процесс решения графически и аналитически. Третья задача выполняется в соответствии со специальностью студента, при этом вариант задачи также формируется студентом самостоятельно исходя из профессиональной деятельности, специальности и полученных знаний при изучении специальных дисциплин. Данные таблиц 5-8 могут носить лишь ориентировочный характер. Стандартные подпрограммы численных методов могут быть взяты из рекомендованного списка источников литературы [2; 8; 9] или из приложения Б настоящих методических указаний. Если работа не зачтена, то студент все исправления выполняет в конце той же тетради после подписи преподавателя, добавляя нужное количество листов. Какие-либо исправления в тексте, уже проверенном преподавателем, не допускаются. Работы, выполненные с нарушением этих правил, не зачитываются, также как и работы, содержащие серьезные ошибки. Задача 1. Разработать математическую модель, алгоритмы и использовать необходимую программу для расчета электрической цепи постоянного тока по заданной схеме. Методические рекомендации Расчет электрической цепи постоянного тока состоит в определении неизвестных токов в ветвях. Решение может быть проведено одним из трех способов: 1) по законам Кирхгофа; 2) методом контурных токов; 3) методом узловых потенциалов.
Таблица 2- Данные к задаче 1
Данные к задаче 2
Задача 3.1- для специальностей -“Механизация сельского хозяйства”, “Технология обслуживания и ремонта машин в АПК”.
Задача 3.2 - для специальностей -“Механизация переработки сельскохозяйственной продукции”, “Технология продуктов общественного питания”.
Задача 3.3 предусмотренадля всех специальностей.
Общая постановка Для изготовления n видов продукции P1,…, Pn предприятие использует m видов ресурсов S1, …, Sm (сырьё, топливо, материалы и т. д.). Запасы ресурсов каждого вида ограничены и равны b1, …, bm. На изготовление единицы продукции j -го вида (j=1, …,n) расходуется aij единиц i -го ресурса (i = 1,…, n). При реализации единицы j -й продукции предприятие получает Cj единиц прибыли. Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль. Пример: (ориентировочный его не переписывать! При выполнении вариантного задания студент формулирует задачу самостоятельно исходя из требований профессиональной деятельности.) АО “КВАНТ” производит 3 вида продукции: спальный гарнитур “КОМФОРТ”, кухонный гарнитур “УЮТ”, мягкую мебель “ОТДЫХ”. При этом использует 4 вида ресурсов: ламинат - (облицованная пластиком ДСП), конферматы - (шурупы-саморезы), гобелен - (мебельная ткань), поролон. Запасы ресурсов составляют: ламината - 25 м2, конферматов - 14 комплектов, гобелена – 19 рулонов, поролона – 24 м2. На изготовление одного спального гарнитура расходуется: ламината – 2 м2, конферматов –1 комплект, гобелена –1 рулон, поролона–3 м2. Для кухонного гарнитура и мягкой мебели данные в таблице 4. При реализации гарнитура “КОМФОРТ” АО “КВАНТ” получает прибыль 600 рублей, гарнитура “УЮТ”-550 рублей, мебели “ОТДЫХ” -750 РУБЛЕЙ. Требуется составить такой план выпуска продукции, чтобы при её реализации АО “ КВАНТ” получило максимальную прибыль.
Таблица 4- Варианты задач об использовании ресурсов
Продолжение таблицы 4
3.2. Задача о смесях К этому типу относятся разнообразные задачи на составление рациона питания, смесей из нескольких компонентов (продуктов, материалов и т.п.) для получения конечного продукта с заданными свойствами. В математическом плане к этому виду относятся также некоторые задачи планирования производства. Рассмотрим формулировку задачи о смеси. Имеется n продуктов P 1,…,P n, содержащих m питательных веществ S1,…, Sm. Пусть a ij, i = 1,…,n; j = 1,…,m, - количество единиц j -го питательного вещества в единице j -го продукта; b j – суточная потребность (минимальная норма) организма в j -м питательном веществе; C 1 – стоимость единицы i- го продукта. Требуется выбрать такой суточный рацион питания (т.е. назначить количество продуктов P 1,… P n, входящих в него), чтобы условия по питательным веществам были выполнены, а стоимость рациона была минимальной. Варианты ориентировочных данных задачи приведены в таблице 5.
Таблица 5. –Данные к задаче о смесях
3.3. Задача о загрузке оборудования Рассмотрим две постановки этой задачи. 1. Предприятие выпускает n видов изделий P 1,…,Pn, каждое из которых проходит последовательную обработку на станках типов T 1,…, T m . Запас мощности станков, т.е. рабочее время станка, составляет соответственно b 1,…, bm единиц времени. Изделие P i обрабатывается первым станком (типа Т1) ai 1 единицвремени, вторым станком – a i 2 единиц времени и т.д. При реализации одно изделие P i приносит предприятию C i единиц прибыли (i = 1,…, n). Составить такой план загрузки станков, при котором предприятие получит максимальную прибыль. Конкретные числовые данные приведены в таблице 6. 2. Предприятию необходимо выпустить n видов изделий P 1,…, Pn в количествах соответственно N1,…, Nn единиц. Для этой цели используются т типов станков T1,…, Tm, каждый из которых может обрабатывать все изделия Pi, i = 1,…, n. Производительность каждого станка (количество изделий, обрабатываемых в единицу времени) имеет величину a i j, i = 1,…,n; j = 1,…, m. Запас мощности станков (рабочее время станка) составляет соответственно b1,…, bm единиц времени. составить такой план загрузки станков, при котором себестоимость выпуска продукции будет минимальной. Ориентрировочные числовые данные приведены в таблице 7. Таблица 6- Первый вариант задачи о загрузке оборудования
Таблица 7- Второй вариант задачи о загрузке оборудования
ПРИЛОЖЕНИЯ
Приложение А
ОСНОВНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ ПАКЕТОВ ПРИКЛАДНЫХ ПРОГРАММ 1. Пакеты, реализующие численные методы решения различных математических задач, применяются во многих областях науки и техники. Специализациями пакетов этого назначения могут быть, например, решения уравнений с частными производными или решения уравнений гидродинамики, а спецификой — повышенная точность вычислений или широкое использование графопостроителя (принтера, плоттера) для вывода результатов. 2. Пакеты для выполнения аналитических вычислений используются в основном в физике
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.132 (0.01 с.) |

 (13)
(13)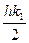 , ti +
, ti +  );
); , ti +
, ti +