
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1 (достаточный признак существования предела последовательности)
Всякая возрастающая ограниченная сверху последовательность имеет предел. Теорема 2 (второй замечательный предел) Последовательность Итак, Так как 2 < an < 3, то 2 < Число e широко используется как основание для показательной функции y=ex (экспонента) и как основание для логарифмов logex=lnx (натуральные логарифмы).
Рассмотрим (рис. 1.13) функцию Рассмотрим применение второго замечательного предела для вычисления некоторых пределов. Решение. Обозначим:
Сравнение бесконечно малых функций.Эквивалентные бесконечно малые функции. Пусть a(x) и b(x) – б.м. функции при x → a (x→ + ∞, x → –∞, x → x0,...). Рассмотрим предел их отношения при x → a. 1. Если 2. Если 3. Если α(x) – б.м. высшего порядка, чем β(x), и 4. Если не существует 5. Если Пример 1. α(x) = (1 – x)3, β(x) = 1 – x3. Очевидно, что при x→1 функции α(x), β(x) являются б.м. Для их сравнения найдем предел их отношения при x →1:
Вывод: α(x) является б.м. высшего порядка, по сравнению с β(x) при x → 1. Нетрудно убедиться, что Пример 2. Функции α1(x) = 4x, α2(x) = x2, α3(x) = sinx, α4(x) = tgx являются бесконечно малыми при x→0. Сравним их:
Теорема 1. Пусть α(x) ~ α1(x), β(x) ~ b1(x) при x → a. Если существует Пример 3. Найти
Теорема 2. Бесконечно малые функции α(x) и β(x) эквивалентны (при x → a) тогда и только тогда, когда α(x) - β(x) является б.м. высшего порядка, по сравнению с α(x) и β(x) (при x → a). Теорема 3. Сумма конечного числа бесконечно малых различных порядков эквивалентна слагаемому низшего порядка. Пример 4. Найти По теореме 3 при x →0: 4x + 2x3 ~ 4x, sin2x + 3tg5x + x3 ~ 3tg5x, тогда
НЕПРЕРЫВНОСТЬ ФУНКЦИИ Пусть функция f(x) определена в точке x0 и некоторой ее окрестности. Если существует На языке логики равенство Используя понятия односторонних пределов, можно перефразировать определение так: функция называется непрерывной в точке x0, если она определена в точке x0 и некоторой ее окрестности, если существуют Если Аналогично определяется непрерывность справа. Пример 1. Функция f(x) = x3 определена на R. Покажем, что f(x) непрерывна в точке x0 = 2. Пример 2. Покажем, что f(x) непрерывна в точке x0 = 0:
Дадим определение точек разрыва. Пусть f(x) определена в окрестности точки x0, но может быть не определена в x0.
Точка x0 разрыва первого рода, для которой 3. Если рассмотреть функцию Рассмотрим операции над непрерывными функциями. Теорема 1. Если функции f1(x) и f2(x) непрерывны в точке x0, то их сумма и произведение также непрерывны в точке x0. Если, кроме того, f2(x0) ≠0, то частное также непрерывно в точке x0. Установим непрерывность некоторых элементарных функций: 1. Всякая постоянная функция y = C непрерывна в каждой точке x0 2. Функция y = x непрерывна в любой точке x0, так как 3. Любой многочлен: y = a0 + a1x + a2x2 +...+ anxn, непрерывен в каждой точке числовой оси, как сумма непрерывных функций. 4. Всякая рациональная дробь, являющаяся отношением двух многочленов 5. Функция y = sinx, y = cosx непрерывны в точке x0 = 0, так как Теорема 3. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Если функция f(x) непрерывна в каждой точке интервала (a, b), то говорят, что f(x) непрерывна на интервале (a, b). Пример 6. Функция
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.108.54 (0.018 с.) |
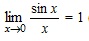 .
. возрастает и ограничена сверху, по теореме 1 существует предел, этот предел называют неперовым числом и обозначают через e.
возрастает и ограничена сверху, по теореме 1 существует предел, этот предел называют неперовым числом и обозначают через e.
 an ≤ 3, т.е. 2 < e ≤ 3. Это число e иррациональное и e ≈2,718282.
an ≤ 3, т.е. 2 < e ≤ 3. Это число e иррациональное и e ≈2,718282.
 , которая не определена на отрезке [-1,0] (подумайте почему?). Ее область определения (–∞, –1)U(0, +∞).
, которая не определена на отрезке [-1,0] (подумайте почему?). Ее область определения (–∞, –1)U(0, +∞). 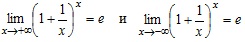 . Нетрудно показать, что
. Нетрудно показать, что 

 . Если n→∞, то m→∞ и мы получим:
. Если n→∞, то m→∞ и мы получим: 
 и b – конечное число, b ≠ 0, то функции α(x), β(x) называются бесконечно малыми одного порядка малости при x → a.
и b – конечное число, b ≠ 0, то функции α(x), β(x) называются бесконечно малыми одного порядка малости при x → a. , то α(x) называют бесконечно малой высшего порядка, чем β(x) при x → a. Очевидно, в этом случае
, то α(x) называют бесконечно малой высшего порядка, чем β(x) при x → a. Очевидно, в этом случае  .
. (b – конечное число, k
(b – конечное число, k 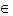 N), то α(x) называют бесконечно малой k-го порядка, по сравнению с β(x) при x → a.
N), то α(x) называют бесконечно малой k-го порядка, по сравнению с β(x) при x → a. (ни конечный, ни бесконечный), то α(x), β(x) называют несравнимыми б.м. при x →a.
(ни конечный, ни бесконечный), то α(x), β(x) называют несравнимыми б.м. при x →a. , то α(x), β(x) называются эквивалентными б.м. при x → a, что обозначается так: α(x) ~ β(x) при x → a.
, то α(x), β(x) называются эквивалентными б.м. при x → a, что обозначается так: α(x) ~ β(x) при x → a.
 (убедитесь!), откуда следует, что α(x) – б.м. 3-го порядка малости, по сравнению с β(x) при x → 1.
(убедитесь!), откуда следует, что α(x) – б.м. 3-го порядка малости, по сравнению с β(x) при x → 1.
 , то существует и
, то существует и  .
.  .
. 
 .
.
 , то функция f(x) называется непрерывной в точке x0, а x0 называется точкой непрерывности функции f(x).
, то функция f(x) называется непрерывной в точке x0, а x0 называется точкой непрерывности функции f(x). описывается формулой:
описывается формулой: 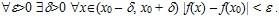
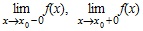 и
и 
 , значит, f(x) = x3 непрерывна в точке x0 = 2.
, значит, f(x) = x3 непрерывна в точке x0 = 2. .
.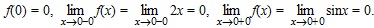
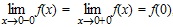 , то непрерывность функции f(x) в точке x0 = 0 доказана.
, то непрерывность функции f(x) в точке x0 = 0 доказана. .
. 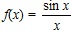 не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x).
не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x).  не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x).
не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x).  и т.д. График y = E(x) представлен на рис. 1.14.
и т.д. График y = E(x) представлен на рис. 1.14.
 .
.  то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.
то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.  . В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0 = 2 является точкой разрыва первого рода, так как
. В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0 = 2 является точкой разрыва первого рода, так как 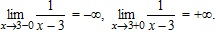 существуют пределы. В примере 4 x0 = 3 – точка разрыва второго рода, так как
существуют пределы. В примере 4 x0 = 3 – точка разрыва второго рода, так как  .
. , то φ(x) непрерывна в точке x0 = 0, так как
, то φ(x) непрерывна в точке x0 = 0, так как  . Доопределив функцию в точке x0 = 0, мы устранили разрыв.
. Доопределив функцию в точке x0 = 0, мы устранили разрыв. .
.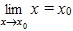 . Тогда функция y = Cxn, где n
. Тогда функция y = Cxn, где n  , непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.
, непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.
 непрерывна на интервалах (–∞, 3) и (3, +∞), так как при x0≠ 3:
непрерывна на интервалах (–∞, 3) и (3, +∞), так как при x0≠ 3:  .
.


