
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение критерия РозенбаумаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Критерий используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. В каждой из выборок должно быть не менее 11 испытуемых. Критерий позволяет быстро оценить различия между двумя выборками по какому-либо признаку. Если критерий Q не выявляет достоверных различий, это еще не означает, что их действительно нет. В этом случае стоит применить критерий φ* – Фишера. Если Q – критерий выявляет достоверные различия между выборками с уровнем значимости a £0,01, можно ограничиться только им. Критерий применяется в тех случаях, когда данные представлены в порядковой шкале. Гипотезы Н0:Уровень признака в выборке 1 не превышает уровня признака в выборке 2. Н1:Уровень признака в выборке 1 превышает уровень признака в выборке 2. Условия применения критерия Q – Розенбаума 1) Измерение может быть проведено в шкале порядка, интервалов или отношений. 2) Выборки должны быть независимыми. 3) В каждой из выборок должно быть не меньше 11 испытуемых (n 1, n 2 ³ 11 и n1 » n2). 4) Должны соблюдаться следующие ограничения: § если n1, n2 £ 50, то должно выполняться ½n1 - n2½£ 10; § если 51 £ n1, n2 £ 100, то должно выполняться ½n1 - n2½£ 20 § если n1, n2 ³ 100, то допускается, чтобы одна из выборок была больше другой не более чем в 1,5-2 раза. 5) Диапазоны разброса значений в двух выборках не должны совпадать между собой, в противном случае применение критерия бессмысленно. Алгоритм подсчета критерия Q – Розенбаума 1. Проверить, выполняются ли ограничения. 2. Упорядочить значения отдельно в каждой выборке по степени убывания признака. Считать выборкой 1 ту выборку, значения в которой предположительно выше. 3. Сформулировать гипотезы. 4. Определить максимальное значение в выборке 2. 5. Подсчитать S1 – количество значений в выборке 1, которые выше максимального значения в выборке 2. 6. Определить минимальное значение в выборке 1. 7. Подсчитать S2 – количество значений в выборке 2, которые ниже минимального значения выборки 1. 8. Подсчитать эмпирическое значение критерия по формуле Qэмп= S1 + S2. (10.1) 9. По таблице 5 Приложения 1определить критические значения Q для данных n1 и n2. 10. Для процесса принятия решения вычертить «ось значимости».
Задача 10.1 У двух групп учащихся из городской школы (14 человек) и городского лицея (12 человек), используя тест Векслера, были измерены показатели интеллекта. Можно ли утверждать, что учащиеся из городского лицея превосходят учащихся из городской школы по показателям интеллекта. Решение Индивидуальные показатели интеллекта по двум группам представлены в таблице 10.2 в порядке возрастания. Так как показатели в группе учащихся лицея выше, то эту группу считаем первой.
Таблица 10.2
Гипотезы к задаче H0: Учащиеся лицея не превосходят учащихся школы по показателям интеллекта. H1: Учащиеся лицея превосходят учащихся школы по показателям интеллекта. Максимальный показатель во второй выборк – 125. Количество показателей первой выборки, которые больше максимального показателя второй выборки: S1 = 6. Минимальный показатель в первой выборке – 94. Количество показателей второй выборки, которые меньше минимального показателя первой выборки: S2 = 5. Эмпирическое значение критерия определяем по формуле (10.1): Qэмп = S1 + S2 = 6 + 5 = 11. По таблице определяем критические значения Q для n1 = 14, n2 = 12:
«Ось значимости»
Ответ Qэмп=11, нулевая гипотеза отклоняется и принимается альтернативная гипотеза. Учащиеся лицея превосходят учащихся школы по показателям интеллекта (a<0,01).
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.189.197 (0.009 с.) |

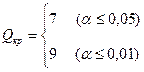 .
.




