
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическая функция совокупного спросаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Эта функция выводится из модели IS-LM. Основные предпосылки: · существуют заданный объем производства предыдущего периода yt -1; · считаем заданными инфляционные ожидания; · домашние хозяйства и фирмы являются рациональными экономическими агентами и делают поправку на ожидаемую инфляцию, тогда реальная ставка процента r/ = r − p te (r − номинальная ставка процента). Уравнение кривой IS:
где x y = Ty + Sy + Imy; Уравнение кривой LM:
где Ly и Lr − предельные склонности к предпочтению ликвидности для сделок и в качестве имущества соответственно, М = МS − Lrr max. Решая совместно уравнения (15.22) и (15.23), получим:
Уравнение для динамической функции совокупного спроса (рис. 15.9) будет
(15.26)
Рис. 15.9. Динамическая функция совокупного спроса Развитие инфляции в результате монетарного импульса Пусть в исходный момент времени экономика находится в состоянии общего экономического равновесия в условиях полной занятости:
В каждый дискретный момент времени существует равенство совокупного спроса и совокупного предложения (экономика находится в равновесии). Пусть, начиная с первого периода, в экономике увеличивается предложение денежной массы ( Для того, чтобы проанализировать процесс перехода к новому устойчивому состоянию, рассмотрим факторы, определяющие направление движения к равновесию (рис. 15.10): · если · если текущий выпуск меньше равновесного, то темп инфляции меньше нуля, если выпуск больше равновесного, то темп инфляции больше нуля, инфляция увеличивается. Складывая вектора, получим направление движения инфляции в каждый момент времени (рис. 15.11).
Рис. 15.10. Направления движения к равновесию
Рис. 15.11. Направления движения инфляции
Таким образом, в результате монетарного импульса (выброса дополнительного количества денежной массы) инфляция развивается по спирали. Экономика приходит к новому равновесному состоянию, в котором темп инфляции равен первоначальному изменению денежной массы (рис. 15.12).
Рис. 15.12. Развитие инфляции при монетарном импульсе Экономический рост и экономические циклы Модели экономического роста Под экономическим ростом национального хозяйства подразумевается такое его развитие, при котором увеличивается реальный национальный доход. Мерой экономического роста служит темп прироста реального национального дохода в целом
или на душу населения. Экономический рост называется экстенсивным, если он не меняет среднюю производительность труда в обществе: Модель Домара Предполагается, что на рынке труда существует избыточное предложение и это обеспечивает постоянство уровня цен. Рынок благ изначально сбалансирован. Фактором увеличения совокупного спроса и совокупного предложения выступает прирост инвестиций. Если в периоде
следовательно, Экономический рост будет равновесным, если
Таким образом, в описанных условиях равновесный рост экономики достигается тогда, когда темп прироста инвестиций равен произведению значений производительности капитала и предельной склонности к сбережению. Значение Так как при равновесии
В результате условие равновесного роста (16.3) можно расширить:
Модель Харрода Если в модели Домара объем инвестиций задается экзогенно (внутри модели), то Харрод включает в свою модель эндогенную функцию инвестиций, основанную на ожиданиях предпринимателей относительно совокупного спроса:
где c = const. Приращение национального дохода предприниматели определяют следующим образом: если в предшествующем периоде спрос превышал предложение (
где r> 1, если Умножим обе части (16.7) на
Совокупный спрос, как и в модели Домара, определяется посредством мультипликатора:
Рост экономики будет равновесным, если совокупное предложение равняется совокупному спросу, т.е.
Пусть в предшествующем периоде было равновесие, т.е.
С учетом (16.11) выражение (16.10) принимает вид
Правая часть уравнения (16.12) определяет величину равновесного темпа прироста в модели Харрода. Темп роста, определяемый по формуле (16.12), Харрод назвал гарантированным темпом роста, так как он гарантирует полное использование существующих производственных мощностей (капитала). Харрод ввел понятие «естественного» темпа роста, под которым понимал такой темп роста капитала и национального дохода, который обеспечивает полную занятость растущего предложения труда. Если в исходном периоде существует полная занятость и капиталовооруженность труда постоянна, как это предполагается в посткейнсианских моделях, то естественный темп роста экономики равен темпу роста трудовых ресурсов. Соотношение между значениями гарантированного и естественного темпов роста определяет состояние экономической конъюнктуры. Если гарантированный темп роста превышает естественный, то вследствие недостатка трудовых ресурсов ожидавшийся предпринимателями темп роста не будет достигнут. В результате объем инвестиций сократится и возникнет депрессия. Когда естественный темп роста превышает гарантированный, фактический темп роста может быть равным гарантированному и экономика окажется в состоянии динамического равновесия при наличии конъюнктурной безработицы. В случае превышения естественного темпа роста над гарантированным фактический темп роста тоже может оказаться выше гарантированного, так как избыток трудовых ресурсов позволяет увеличивать инвестиции. Тогда фактический объем производства превысит ожидаемый, стимулируя дальнейший рост инвестиций. Модель Солоу В 1956 г. Солоу описал модель, которая показывает взаимосвязь сбережений, накопления капитала и экономического роста. Исходным пунктом анализа является производственная функция, представленная уравнением Q = Q (K,L,T), (16.13) где K – капитал; L – труд; T – технология. Выразим все переменные в виде показателей на душу населения. Введем обозначения:
Уравнение (16.13) показывает, что выпуск на душу населения является возрастающей функцией отношения «капитал-труд». Такой вид производственной функции, когда все показатели выражены в расчете на душу населения, показан на рис. 16.1. Как видно из рисунка, большему значению
Рис. 16.1. Производственная функция на душу населения Будем рассматривать случай закрытой экономики без государства, что было сделано в оригинальной версии Солоу. В этом случае отечественные инвестиции
Изменения основных производственных фондов равны чистым инвестициям за вычетом амортизации. Предположим, что для основных производственных фондов объема
Предположим также, что сбережения составляют фиксированную долю общего объема национального (совокупного) выпуска, т.е.
Если разделить обе части этого выражения на суммарное количество рабочей силы, то получим
Предположим, что население растет с постоянным темпом l, который определяется биологическими и другими факторами, лежащими вне модели, тогда
Таким образом,
Подставив это выражение в уравнение (16.18), получим основное уравнение накопления капитала:
Определенная часть сбережений на душу населения должна быть использована для обеспечения каждого из вновь вступающих в состав рабочей силы капиталом Сбережения, направляемые на оснащение рабочих мест, называются сбережениями, идущими на расширение капитала (под словом «расширение» здесь подразумевается увеличение числа работающих). Сбережения, используемые для увеличения отношения «капитал выпуск», называются сбережениями, идущими на рост фондовооруженности (увеличение капитала на одного работающего). Таким образом, основное уравнение накопителя капитала (16.21) констатирует, что сбережения, идущие на рост фондовооруженности равны среднедушевые сбережениям плюс сбережения, идущие на расширение капитала. Теперь рассмотрим случай устойчивого (стационарного) состояния, или положения долгосрочного равновесия. В устойчивом состоянии объем капитала на одного работающего достигает своего равновесного значения и больше не меняется, постоянно оставаясь на этом уровне. В результате этого объем выпуска на одного работающего также находится в устойчивом состоянии (технологические изменения на данный момент не учитываются). Таким образом, в устойчивом состоянии как k, так и q постоянно находятся на одном и том же уровне. Для достижения устойчивого состояния необходимо, чтобы выполнялось точное равенство среднедушевых сбережений и сбережений, идущих на расширение капитала, чтобы D k = 0. Формально это можно записать в виде
Теория экономических циклов Экономическая цикличность − это объективная форма развития рыночной экономики. Она представляет собой волнообразное движение хозяйственной конъюнктуры (деловой активности) при регулярном чередовании ее подъемов и спадов (от кризиса до кризиса). Под экономическим циклом подразумевается период развития экономики между двумя одинаковыми состояниями конъюнктуры. Считая циклы признаком макроэкономической нестабильности рынка, следует иметь в виду, что они выражаются в органическом единстве периодически повторяющихся процессов не только нарушения равновесного состояния экономики, но и его последующего естественного восстановления. Без экономических потрясений (кризисов) рыночная система не могла бы развиваться. Отправной точкой циклического развития рыночной экономики с некоторой долей условности можно считать 1825 г., когда в Англии разразился первый кризис перепроизводства. Он положил начало периодическим колебаниям экономической конъюнктуры, которые достаточно регулярно повторялись в течение всего XIX в. со средним промежутком 8-10 лет. Постепенно в русло цикличности вовлекались и другие страны. Самым глубоким и наиболее продолжительным в XIX в. явился мировой экономический кризис 1873-1878 гг. В XX в. побил все рекорды по глубине экономического спада мировой кризис 1929-1933 гг. (так называемая «великая депрессия»). В этот период общий объем промышленного производства ведущих стран мира сократился на 46%, внешнеторговый оборот − на 67%, число безработных достигло 26 млн. человек (почти четвертая часть всех занятых в сфере материального производства), а реальные доходы населения уменьшились в среднем на 58%. С тех пор экономические циклы становятся объектом особого пристального изучения.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.49.19 (0.008 с.) |

 , (15.24)
, (15.24) ; A=Iir* + G + Ex; r* − предельная эффективность капитала; Ii − предельная склонность к инвестированию.
; A=Iir* + G + Ex; r* − предельная эффективность капитала; Ii − предельная склонность к инвестированию. , (15.25)
, (15.25) , где
, где  .
.

 .
. ). В этом случае происходит динамический процесс развития инфляции. В каждый момент времени меняется темп инфляции и уровень выпуска.
). В этом случае происходит динамический процесс развития инфляции. В каждый момент времени меняется темп инфляции и уровень выпуска. , то совокупный выпуск растет, если
, то совокупный выпуск растет, если 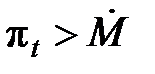 , совокупный выпуск падает, стремясь к равновесному уровню;
, совокупный выпуск падает, стремясь к равновесному уровню;

 , (16.1)
, (16.1)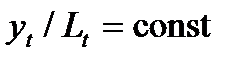 , или
, или  . Когда рост национального дохода опережает рост числа занятых в производстве
. Когда рост национального дохода опережает рост числа занятых в производстве  , имеет место интенсивный рост. Интенсивный рост экономики – основа роста благосостояния населения и условие уменьшения дифференциации в доходах различных социальных слоев.
, имеет место интенсивный рост. Интенсивный рост экономики – основа роста благосостояния населения и условие уменьшения дифференциации в доходах различных социальных слоев. инвестиции возросли на
инвестиции возросли на  , то в результате мультипликационного эффекта в этом периоде совокупный спрос увеличится на
, то в результате мультипликационного эффекта в этом периоде совокупный спрос увеличится на  . Предложение в периоде
. Предложение в периоде 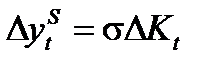 , где
, где  − предельная производительность капитала, которая при данном уровне развития техники предполагается неизменной;
− предельная производительность капитала, которая при данном уровне развития техники предполагается неизменной;  − приращение капитала на начало периода
− приращение капитала на начало периода  , в предшествующем периоде необходимо было осуществить определенный объем инвестиций:
, в предшествующем периоде необходимо было осуществить определенный объем инвестиций: , (16.2)
, (16.2) .
. , т.е.
, т.е. или
или  . (16.3)
. (16.3)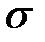 объективно задано технологией производства, и поэтому регулировать темп равновесного роста можно только посредством
объективно задано технологией производства, и поэтому регулировать темп равновесного роста можно только посредством  .
. , а
, а  , причем
, причем  , то
, то 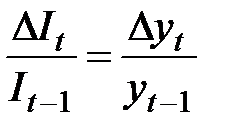 . Поскольку
. Поскольку  , то
, то  . И, наконец, учитывая, что в модели используется производственная функция с невзаимозаменяемыми факторами
. И, наконец, учитывая, что в модели используется производственная функция с невзаимозаменяемыми факторами  , темп прироста предложения труда должен равняться темпу прироста капитала:
, темп прироста предложения труда должен равняться темпу прироста капитала: . (16.4)
. (16.4) . (16.5)
. (16.5) , (16.6)
, (16.6) ), то предприниматели увеличивают темп расширения производства; при
), то предприниматели увеличивают темп расширения производства; при  темп роста производства уменьшается, и при
темп роста производства уменьшается, и при  темп роста продукции остается неизменным. Формально это записывается так:
темп роста продукции остается неизменным. Формально это записывается так: , (16.7)
, (16.7) ; r< 1, если
; r< 1, если  ; r = 1, если
; r = 1, если 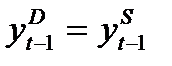 .
. и прибавим
и прибавим 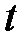 :
: . (16.8)
. (16.8) . (16.9)
. (16.9) . (16.10)
. (16.10) . (16.11)
. (16.11) или
или  . (16.12)
. (16.12) − выпуск на одного работающего;
− выпуск на одного работающего;  − количество капитала на единицу труда. Тогда производственную функцию можно записать в виде
− количество капитала на единицу труда. Тогда производственную функцию можно записать в виде . (16.14)
. (16.14)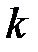 соответствует большее значение
соответствует большее значение  , однако
, однако  равны национальным сбережениям
равны национальным сбережениям  :
: . (16.15)
. (16.15) амортизация составляет постоянную долю
амортизация составляет постоянную долю  , равную
, равную  . В этом случае изменение общего объема производственных фондов равно инвестициям минус амортизация:
. В этом случае изменение общего объема производственных фондов равно инвестициям минус амортизация: . (16.16)
. (16.16) . Следовательно,
. Следовательно, . (16.17)
. (16.17) . (16.18)
. (16.18) . Для начала примем технический прогресс равным нулю. Поскольку
. Для начала примем технический прогресс равным нулю. Поскольку  , темп роста
, темп роста  . (16.19)
. (16.19) . Теперь, разделив обе части уравнения на L, получим
. Теперь, разделив обе части уравнения на L, получим . (16.20)
. (16.20) . (16.21)
. (16.21) . (16.22)
. (16.22)


