
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В межвременном выборе домашних хозяйствСодержание книги
Поиск на нашем сайте
Бюджетное ограничение для многих периодов выводится аналогичным образом. Запишем двухпериодное ограничение и ограничение для третьего периода:
Отсюда находим B2 и подставляем в первое уравнение:
Бюджетное ограничение для j периодов имеет вид:
Эта формула описывает так называемый «конечный горизонт» планирования домашних хозяйств. Когда домашние хозяйства делают выбор для j периодов, говорят о моделях «жизненного цикла». Если после жизненного цикла индивидуум не оставляет ни долгов, ни сбережений, тогда
совокупные доходы равны совокупным расходам. Кейнсианский подход к теории потребления При выведении функции совокупного потребления Кейнс исходил из гипотезы «абсолютного дохода», в соответствии с которой потребление зависит от абсолютной величины текущего дохода. Однако Кейнс подчеркивал (и это подтверждено эмпирическими исследованиями), что «люди склонны увеличивать свое потребление с ростом дохода, но не в той же мере, в какой растет доход». Кейнс создал простую модель, связывающую текущий доход и текущее потребление: C = C0 + Cy y; C0 > 0; 0 < Cy < 1, (11.10) где C0 − величина автономного (независимого от текущего дохода) потребления, при y = 0 автономное потребление осуществляется за счет сокращения имущества; Cy = MPC − предельная склонность к потреблению (показывает пропорцию изменения потребления по отношению к изменению в располагаемом доходе). Средняя норма потребления APC = C/y (доля всего располагаемого дохода, который потребляется) по мере роста дохода снижается, стремясь к постоянной предельной склонности к потреблению (рис. 11.9).
Рис. 11.9. Средняя и предельная норма потребления как функция от дохода
Функция сбережения в кейнсианской модели S = S0 + Sy y; S0 < 0; 0 < Sy < 1, (11.11) где S0 – отрицательный уровень сбережений в отсутствии дохода; Sy = MPS − предельная склонность к сбережению (показывает пропорцию изменения сбережений по отношению к изменению в располагаемом доходе).
, (11.12)
Пример. Пусть C = 0,75; S = 0,25; C0 = 250. Отсюда S0 = -250. Имеем следующие зависимости для функций потребления и сбережения: C = 250 + 0,75 y; S = -250 + 0,25 y. Эти зависимости можно изобразить графически (рис. 11.10). В области, где потребление превышает доход, сбережения отрицательны, а в области, где доход превышает потребление, − положительны.
Рис. 11.10. Функции потребления и сбережения (кейнсианский подход)
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.143.202 (0.007 с.) |

 , (11.5)
, (11.5) . (11.6)
. (11.6) . (11.7)
. (11.7) (11.8)
(11.8)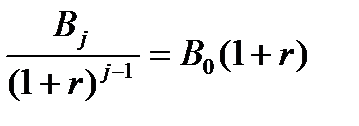 , (11.9)
, (11.9)


