
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Семь простых японских методовСодержание книги
Поиск на нашем сайте В процессе изготовления изделия существует множество факторов, оказывающих влияние на его показатели качества. Оценивая производственный процесс с точки зрения изменения качества, можно рассматривать его как некую совокупность причин изменчивости. Эти причины и приводят к появлению, как бездефектных изделий, так и дефектных. Если деталь соответствует чертежу (стандарту) она бездефектна, если нет, то – дефектна. Сплошной контроль качества изделий в массовом производстве: во-первых, не обеспечивает гарантию 100% качества, а во-вторых, является очень затратным. Применение статистических методов – весьма действенный путь разработки новой технологии и контроля качества производственных процессов. Многие ведущие фирмы активно используют статистические методы и считают целесообразным тратить до 100 часов в год на обучение сотрудников этим методам. Статистические методы управления качеством – это философия, политика, система, методология, а также технические средства управления качеством на основе измерений, анализа, испытаний, контроля, данных по эксплуатации, экспертных оценок и любой другой информации, позволяющей принимать, достоверные, обоснованные, доказательные решения. Информация должна быть своевременной, объективной и достоверной. Массовое применение получили следующие статистические методы: 1. Контрольные листки; 2. Графики и диаграммы на плоскости; 3. Диаграмма Парето; 4. Расслоение (стратификация), диаграммы разброса (рассеяния); 5. Диаграмма Исикавы («рыбья кость»); 6. Гистограммы; 7. Контрольные карты (Шухарта). Широкое внедрение в практику работы российских предприятийсеми простых японских методов – необходимое условие быстрого прогресса в производстве качественной продукции. Этот шаг не требует значительных затрат, если только не считать организации широкомасштабного обучения рабочих и специалистов статистическим методам и внедрения их в производство. Обучение и организация производства плюс система стимулирования за качество – вот ключевые моменты российского качества. Рекомендации по применению семи простых японских методов 1. Необходимо четко определить источник данных (где собираются данные: рабочее место, станок, рабочий; кто собирает данные: контролер, рабочий; периодичность сбора данных: каждая 5-я деталь, 1-я смена, каждый час и т.п.; материал, из которого изготавливают детали: марка, партия; и т.д. 2. Необходимо подобрать метод измерения, приборы и контрольные приспособления. Очевидно, что средства измерения и контрольные приспособления должны быть аттестованы (поверены), а персонал должен быть обучен. 3. Необходимо определить перечень всех характеристик, которые подлежат измерению. 4. Необходимо разработать простую и удобную для дальнейшей обработки данных форму их регистрации. Рекомендуется использовать количественные данные. Контрольные листки Контрольный листок – это бумажный бланк, на котором заранее напечатаны контролируемые параметры и форма, куда необходимо заносить параметры. Это делается для того, чтобы можно было легко и точно записывать данные измерений. При необходимости на контрольном листке может быть приведен эскиз детали или схема, на которых делаются пометки, показывающие местонахождение дефектов (например: контрольный листок локализации дефектов). На контрольном листке обязательно должна быть следующая информация: - наименование и обозначение детали, номер партии (заказа), из которой взяты детали, общее количество проверенных деталей; - обозначение техпроцесса, производственная операция; - номер цеха, участка, где изготавливались детали; - марка станка и его заводской номер; - марка материала, из которого изготавливались детали; - дата и время изготовления деталей, рабочая смена; - фамилии рабочих, изготовивших детали и их квалификация; - фамилия, работника, проводившего измерения и заполнение формы и его квалификация; - информация о методике и средствах измерения (марка измерительного прибора, заводской номер, контрольное приспособление и т.п.) Графики и диаграммы на плоскости Наиболее распространенными средствами наглядного представления количественных данных являются графики и диаграммы. С их помощью можно объединять большие объемы информации, используя при этом небольшие участки бумаги, и сообщать результаты анализа определенной комплексной проблемы наглядно, сжато и ясно. Примерами могут служить: - линейные графики; - столбчатые диаграммы; - круговые диаграммы. Диаграмма Парето Причины изменений качества бесчисленны, а их воздействие на качество различно. Все возможные причины можно разделить на две группы: - «немногочисленные существенно важные», которые оказывают существенное воздействие на качество; - «многочисленные несущественные», охватывающие большое количество причин, но незначительно воздействующие на качество. Очевидно, что при проведении анализа причин появления дефектов необходимо найти существенно важные причины, вызывающие появление дефектов, выделить и устранить их. Массивы различных данных трудно анализировать, пока они не представлены в наглядной и понятной форме. Анализ Парето - это метод классификации причин возникновения дефектов на «немногочисленные существенно важные» и «многочисленные несущественные». В большинстве случаев подавляющее число дефектов и связанных с ними потерь возникает из-за относительно небольшого количества причин. Анализ Парето ранжирует отдельные области по значимости или важности и дает возможность выявить и в первую очередь устранить те причины, которые вызывают наибольшее количество проблем (несоответствий). Схема, построенная на основе группирования по дискретным признакам, ранжированная в порядке убывания (например, по частоте появления) и показывающая кумулятивную (накопленную) частоту, называется диаграммой Парето (рис. 3).
Рис. 3 Пример диаграммы Парето 1 – ошибки в процессе производства; 2 – некачественное сырье; 3 – некачественные орудия труда; 4 – некачественные шаблоны; 5 – некачественные чертежи; 6 – прочее; А – относительная кумулятивная (накопленная) частота, %; n – число бракованных единиц продукции. Приведенная диаграмма построена на основе группирования бракованной продукции по видам брака и расположения в порядке убывания числа единиц бракованной продукции каждого вида. Она позволяет произвести сравнение ранжированных факторов, определяющих проблемы качества. Диаграмму Парето можно использовать очень широко. С ее помощью можно оценить эффективность принятых мер по улучшению качества продукции, построив ее до и после внесения изменений. Анализ Парето - представляет собой один из инструментов для идентификации и концентрации внимания на немногочисленных жизненно важных факторах, влияющих на качество (иллюстрируется диаграммой Парето). Расслоение (стратификация) Распределение полученных данных на отдельные группы (слои) по определенному признаку в зависимости от выбранного фактора называется расслоением или стратификацией. В качестве стратифицирующего фактора могут быть выбраны любые параметры, определяющие особенности условий возникновения и получения данных. Расслоение можно осуществить: - по исполнителям (по полу, стажу работы, квалификации и т.д.); В торговле может быть осуществлено расслоение по районам, фирмам, продавцам, видам товара, сезонам и т.п. Расслоение помогает выяснить причину появления дефекта, если обнаруживается разница в данных между слоями. При подготовке к сбору данных по какой либо проблеме необходимо тщательно продумать разделение данных на группы при их занесении в форму. Диаграмма разброса (рассеяния) применяется для выявления зависимости (корреляции) одних показателей от других или для определения степени корреляции между n парами данных для переменных x и y: (x1,y1), (x2,y2),..., (xn, yn). Эти данные наносятся на график (диаграмму разброса), и для них вычисляется коэффициент корреляции по формуле где n – размер выборки (количество пар данных – хi и уi); Рассмотрим различные варианты диаграмм разброса (или полей корреляции) на рис. 4.
Рис. 4 Варианты диаграмм разброса. В случае: а) можно говорить о положительной корреляции (с ростом x увеличивается y); б) проявляется отрицательная корреляция (с ростом x уменьшается y); в) при росте x y может как расти, так и уменьшаться, говорят об отсутствии корреляции. Но это не означает, что между ними нет зависимости, между ними нет линейной зависимости. Очевидная нелинейная (экспоненциальная) зависимость представлена и на диаграмме разброса г). Коэффициент корреляции всегда принимает значения в интервале Для тех же n пар данных (x1,y1), (x2,y2),..., (xn, yn) можно установить зависимость между x и y. Формула, выражающая эту зависимость, называется уравнением регрессии (или линией регрессии), и ее представляют в общем виде функцией у = а + bх. Для определения линии регрессии (рис.5) необходимо статистически оценить коэффициент регрессии b и постоянную a. Для этого должны быть выполнены следующие условия: 1) линия регрессии должна проходить через точки (x,y) средних значений x и y. 2) сумма квадратов отклонений от линии регрессии значений y по всем точкам должна быть наименьшей. 3) для расчета коэффициентов а и b используются формулы Т.е. уравнением регрессии можно аппроксимировать реальные данные.
Рис. 5 Пример линии регрессии.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.009 с.) |



 ,
, ,
, ,
,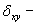 ковариация;
ковариация; стандартные отклонения случайных переменных x и у;
стандартные отклонения случайных переменных x и у; и
и  – среднеарифметические значения хi и уi cоответственно.
– среднеарифметические значения хi и уi cоответственно.
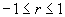 , т.е. при r>0 – положительная корреляция, при r=0 – нет корреляции, при r <0 – отрицательная корреляция.
, т.е. при r>0 – положительная корреляция, при r=0 – нет корреляции, при r <0 – отрицательная корреляция.
 .
.



