
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классический метод расчета переходных процессов основан на непосредственном решении системы дифференциальных уравнений, составленных для электрической цепи на основе законов Кирхгофа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В этом случае решение ищется в виде ik(t)= ik(t)свободная + ik(t)установившееся Свободная составляющая действует в цепи при отсутствии источника в свободном режиме и является общим решением однородного дифференциального уравнения. Установившаяся составляющая устанавливается источником, теоретически при t→∞ и является частным решением неоднородного уравнения, т.е. определяется правой частью уравнения. Может быть постоянной, если действует источник постоянного тока, гармонической, если гармонического тока(~) и периодической, если периодического тока (напряжения). Запишем общее решение однородного дифференциального уравнения
Готовое решение проверяют при t=0 и t→∞, сравнивая с результатами, которые получаются по схемам замещения при тех же моментах времени. Анализ переходных процессов в RLC цепях классическим методом Последовательные и параллельные RL и RC цепи
  
           RL RC RL RC
t=0_ (1) независимые начальные условия i(0_)=0=i(0) 1закон коммутации uc(0_)=0=uc(0) 2 закон коммутации t=0
t=∞
Используя начальные условия
Для оценки временных свойств цепи вводят понятие «постоянной времени».
Постоянные времени показывают за какой промежуток времени свободная экспоненциальная составляющая уменьшится по абсолютной величине в e раз. За 3τ уменьшение идет в 20раз, за 5τ ≈100раз →длительность переходного процесса оценивают величиной (3-5)τ. За 3τ процесс заканчивается на 95%; за 5τ на 99%.
Если отключить источник, то (в зависимости от того как отключать) 1) размыкаем i=0 эл. дуга←энергия с катушки. В RC емкость будет держать некоторое время заряд.
   
Если отключить на перемычку то все процессы пойдут в обратную сторону. Переходные процессы в RLC цепях Последовательная RLC цепь Подключение источника постоянного напряжении
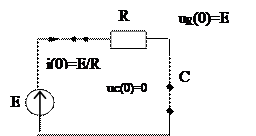
Независимые начальные условия i(0-) = 0 = i(0) uc(0-) = 0 = uc(0). 2. t = 0 зависимые н. у. uR(t) + uL(t) + uc(t) = E 0 + uL(0) + 0 = E 3. t®¥ i(¥) = 0=iУСТ uR(¥) = 0 uL(¥) = 0 uc(¥) = E
Определим коэффициенты А1 и А2. t=0
Окончательно получаем:
4) Определим напряжения uR, uL, uC.
В зависимости от сопротивления R различают различные режимы работы цепи. 1)
Такой режим работы называют апериодическим. 2) R=Rкр – критический режим работы
Графики примерно такие же, но более резкие.
3) Корни p1 и p2 комплексно сопряженные.
Режим переходного процесса называется колебательным. Происходит зарядка и разрядка конденсатора. В цепи происходит обмен магнитной и электрической энергиями.
Найдем выражение для емкости Составим второе уравнение для определения неизвестных коэффициентов:
Из нулевых начальных условий i(0)=0, uC(0)=0 получим систему уравнений:
Поскольку После преобразований получим уравнение:
Последнее выражение приведем к виду:
Переходное напряжение на емкости:
Представим на графике соответствующие переходные напряжения:
Квазипериод свободных колебаний:
Декремент ослабления (затухания):
Логарифмический декремент ослабления:
Напряжение при переходном процессе в колебательном режиме может превысить ЭДС– это надо учитывать. Физическое пояснение колебательного процесса
Колебания возникают, когда есть хорошая возможность обмена энергией разных видов – здесь при малом сопротивлении магнитная энергия индуктивности легко переходит в электрическую энергию емкости и наоборот. Отключение источника в последовательной RLC-цепи Все процессы идут в обратном направлении: емкость разряжается. Характер процесса также определяется корнями характеристического уравнения (сравниваются R и Rкр). Ток меняет направление, соответственно uR и uL меняют знак, а uC остается того же знака.
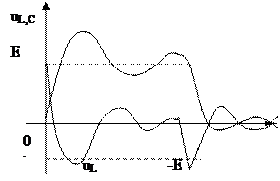
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 где Pm - корни характеристического (вспомогательного) уравнения, соответствующего дифференциальному, а AКm - множители, определенные с применением начальных и конечных условий.
где Pm - корни характеристического (вспомогательного) уравнения, соответствующего дифференциальному, а AКm - множители, определенные с применением начальных и конечных условий.
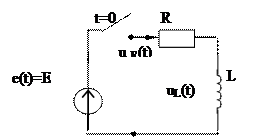
 2 закон Киргофа
2 закон Киргофа





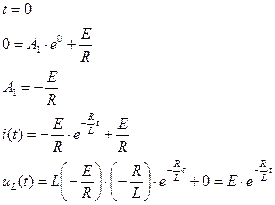





 i
i

 p2+(R/L)p+(1/LC)=0
p2+(R/L)p+(1/LC)=0 Корни уравнения:
Корни уравнения: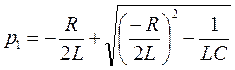





 Проверка
Проверка 


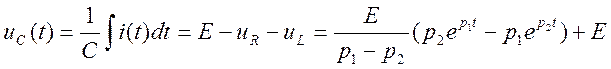
 . Получаем, что p1 и p2 – вещественные, отрицательные.
. Получаем, что p1 и p2 – вещественные, отрицательные.

 = р<0
= р<0



 , где
, где  - частота свободных колебаний (ω0 – резонансная частота).
- частота свободных колебаний (ω0 – резонансная частота).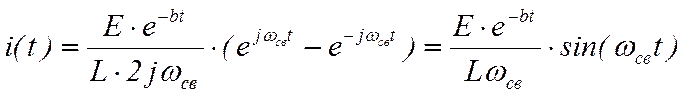 - убывающая по экспоненте синусоида.
- убывающая по экспоненте синусоида.
 – переходное напряжение на резисторе;
– переходное напряжение на резисторе;


 – переходное напряжение на индуктивности.
– переходное напряжение на индуктивности. .
. .
. ,
,  ,
,  .
. , то
, то  ,
,  .
. , откуда
, откуда  .
. , следовательно
, следовательно 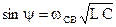 .
.
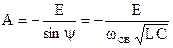 ,
, ,
,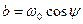 .
. , где
, где  ;
;
 .
. .
. .
. .
.



