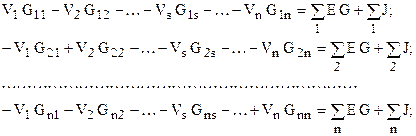Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжений на источниках тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общая стандартная форма записи системы уравнений по МКТ для резистивных цепей с источниками постоянного действия
Здесь: Inn (InK) – соответствующие контурные токи, R11 –собственное контурное сопротивление первого контура, равное сумме сопротивлений элементов входящих в 1 контур, R22 –контурное сопротивление второго и т.д.; R12 – взаимное сопротивление между первым и вторым контурами (учитывается с +, если контурные токи совпадают и с “- ”, если не совпадают) и аналогично; E11 – контурная ЭДС 1 контура, которая содержит алгебраическую сумму ЭДС входящих в 1-ый контур (c + если совпадает с контурным током) и включает влияние источников тока на контур (после переноса из левой части). Далее аналогично. Причем обычно R12 = R21 а если есть управляемые источники, то R12 и R21 могут быть не равны. 6. Применение МКТ Целесообразно применять для сложных схем с несколькими однотипными источниками, у которых частота одна и та же. Если есть L - и C -элементы и частоты источников одинаковые, то применяется в комплексной форме. Если частоты действия разные, то можно применять совместно с методом наложения для расчета частичных токов. 1.8. Метод узловых напряжений (МУН) В качестве основных неизвестных используются так называемые узловые напряжения – это напряжения между узлом схемы или цепи и некоторым опорным или базисным узлом, который выбирается один для всей цепи или схемы. В качестве дополнительных неизвестных используются токи в некоторых «вырожденных» ветвях, которые содержат только идеальные источники напряжения (или ЭДС) без других элементов. Система уравнений по МУН составляется на основе первого закона Кирхгофа. Второй закон и закон Ома используются как вспомогательные. 2. Определение количества уравнений и выбор базисного узла Количество уравнений определяется по формуле:
Базисный узел выбирается из узлов, прилегающих к ветви «вырожденной» (где есть одиночный идеальный источник напряжения) и отмечается знаком заземления или корпуса. I1 E1
Из этих двух узлов обычно берут тот узел, где больше подходит ветвей. Берут там, где удобнее при взгляде на схему. Начинается метод с определения числа «вырожденных» ветвей и базисного узла, потом составляется и решается система уравнений.
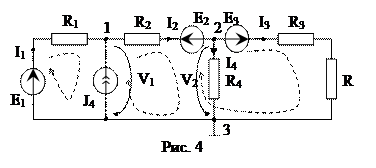
1. При расчёте цепи по методу узловых напряжений определяем число узлов схемы. Один из этих узлов принимаем за базисный. Остальные узлы называются независимыми. Базисный узел – это узел от которого ведется отсчет. Его выбирают в первую очередь там, где есть ветвь, содержащая только одиночный идеальный источник ЭДС, и сходится много ветвей или это тот узел, который удобнее для наглядности (в нашей схеме это узел 3). Базисный узел часто заземляют, при этом его потенциал (напряжение) равен нулю V3=0. Из свойств идеального источника напряжения, следует отметить, что если в схеме имеются ветви, состоящие из одиночных идеальных источников напряжения, то их сопротивление равно нулю, а проводимость – бесконечности. В нашем случае таких ветвей нет NE=0. Для ветвей с источниками тока все наоборот. 2. Определяем число независимых уравнений, составляемых методом узловых напряжений NМУН=NУЗ-1-NЕ=2. Составляем систему алгебраических уравнений методом узловых напряжений, согласно первому закону Кирхгофа. I1+J4-I2=0 I2-I3-I4=0 4. V1,V2 – узловые напряжения узлов 1 и 2 соответственно. Выражаем токи ветвей через узловые напряжения на основе 2 закона Кирхгофа для вспомогательных контуров, которые обязательно проходят через базисный узел, и закона Ома: I1∙R1+V1 =E1, I2∙R2+V2-V1= -E2, I3∙(R3+R)-V2 =E3 (V=U).
После подстановки формул токов данная система уравнений переводится в систему узловых уравнений, записанную в канонической форме. Число уравнений должно быть равно числу неизвестных узловых напряжений. Для 1 уравнения получим
где
IУ1, IУ2 – собственные или задающие узловые токи, соответственно, независимых узлов 1 и 2. В общем виде их можно представить в следующем виде:
где
Узловое напряжение – это напряжение между независимым и базисным узлами и направлено оно к базисному узлу. V1,V2 – узловые напряжения узлов 1 и 2 соответственно. Знак "+" перед узловым напряжением берётся, если это собственное узловое напряжение, в противном случае берётся знак "–". Данную систему решаем методом Крамера. Составляем определитель второго порядка, в первую и вторую строки которого ставим значения проводимостей стоящих при напряжениях, соответственно в первом и во втором уравнениях нашей системы.
После чего вычисляем напряжение
6. Находим токи ветвей через узловые напряжения:
Общая форма записи системы уравнений по МУН с узловыми напряжениями (потенциалами) VK, собственными проводимостями узлов GKK, взаимными проводимостями между узлами GKM и узловыми токами.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2882; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 Записывают уравнения и в матричном виде. Например,
Записывают уравнения и в матричном виде. Например, .
. , где NE – число «вырожденных» ветвей которые содержат только идеальные источники напряжения (или ЭДС) без других элементов.
, где NE – число «вырожденных» ветвей которые содержат только идеальные источники напряжения (или ЭДС) без других элементов.
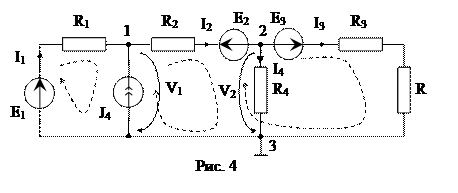 Пример расчета цепи с помощью метода узловых напряжений по схеме
Пример расчета цепи с помощью метода узловых напряжений по схеме
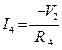
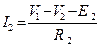
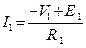

 . Затем можно поменять знаки и получить уравнение
. Затем можно поменять знаки и получить уравнение  . Аналогично для 2 уравнения получим
. Аналогично для 2 уравнения получим . Эти уравнения приводят к стандартному каноническому виду:
. Эти уравнения приводят к стандартному каноническому виду:
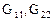 – это собственные проводимости соответственно узлов 1 и 2.
– это собственные проводимости соответственно узлов 1 и 2. .
. .
.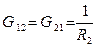 – взаимные проводимости между узлами 1 и 2.
– взаимные проводимости между узлами 1 и 2.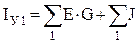 ,
, ,
, – алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 1, на их проводимости,
– алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 1, на их проводимости, 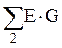 – алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 2, на их проводимости; при этом со знаком "+" берутся те ЭДС, которые действуют в направлении узла, и со знаком "–" – в направлении от узла;
– алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 2, на их проводимости; при этом со знаком "+" берутся те ЭДС, которые действуют в направлении узла, и со знаком "–" – в направлении от узла; 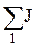 – алгебраическая сумма токов источников тока, присоединенных к узлу 1,
– алгебраическая сумма токов источников тока, присоединенных к узлу 1,  – алгебраическая сумма токов источников тока, присоединенных к узлу 2; при этом со знаком "+" берутся те токи, которые направлены к узлу, а со знаком "–" в направлении от узла. Для нашего случая токи IУ1, IУ2 имеют следующий вид:
– алгебраическая сумма токов источников тока, присоединенных к узлу 2; при этом со знаком "+" берутся те токи, которые направлены к узлу, а со знаком "–" в направлении от узла. Для нашего случая токи IУ1, IУ2 имеют следующий вид: .
. .
. Затем составляем определитель
Затем составляем определитель 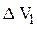 , для этого в определителе
, для этого в определителе  в первом столбе значения проводимостей заменяем значениями токов, стоящих в правой части нашей системе.
в первом столбе значения проводимостей заменяем значениями токов, стоящих в правой части нашей системе. по следующей формуле:
по следующей формуле: Аналогично находим напряжение
Аналогично находим напряжение