Где модуль комплексной частотной характеристики имеет техническое название амплитудно-частотная характеристика (ачх), а угол – фазо - частотная характеристика (фчх).

АЧХ показывает как изменяется отношение амплитуд выходного и входного сигнала электрической цепи при гармоническом воздействии. фазо - частотная характеристика (ФЧХ) показывает как изменяется разность фаз выходного и входного сигнала электрической цепи при гармоническом воздействии. (Все это при изменении частоты.) Частотная характеристика показывает частотные свойства электрической цепи.

Методы расчета передаточных функций

При расчете передаточных функций используются законы Ома и Кирхгофа в операторной и комплексной форме в зависимости от характеристики. Для сложных цепей приминаются некоторые специальные методы: метод контурных токов, метод узловых напряжений и т.п.

Временные характеристики электрических цепей

Под ними понимают функции времени численно равные реакции электрической цепи на стандартное воздействие на цепь. Применяются обычно для линейных цепей при нулевых условиях (без запаса энергии в цепи).

1. Единичная ступенчатая функция или функция Хевисайда. Определяется следующим способом:

σ(t) =1(t)

σ(t) = 0, t<0

σ(t) = 1, t>0

2. Единичная импульсная функция или функция Дирака.

δ(t)=0, t<0

δ(t)= ¥, t=0

δ(t)=0, t>0

Ее можно рассматривать как предел импульсного сигнала такого вида:

t_U=Δt, U_u=1/Δt, Δt→0

В соответствии с испытательными (стандартными) сигналами используются две характеристики:

1. Переходная характеристика - это функция времени, численно равная реакции электрической цепи на единичное ступенчатое воздействие.

h(t) = k(t) = g_σ(t)

Различают в зависимости от типа воздействия и реакции четыре вида переходных характеристик: по напряжению, по току, по сопротивлению и по проводимости.

Размерность переходной характеристики определяется отношением размерности реакции цепи к размерности воздействия.

· по напряжению и по току - безразмерные.

· по сопротивлению - Ом.

· по проводимости - См (сименс).

2. Импульсная характеристика - это функций времени, численно равная реакции электрической цепи на единичное импульсное воздействие.

Обозначается: g_δ(t) = h_δ(t).

Существует также четыре вида импульсных характеристик: по напряжению, по току, по сопротивлению и по проводимости.

Размерность определяется отношением размерностей реакций цепи к размерности площади воздействия. Все импульсные характеристики имеют размерности.

Например, по напряжению - с^-1.

Методики расчета временных характеристик

Переходная характеристика.

· Можно рассчитать классическим методом, подключая ко входу цепи (t=0) источник напряжения (1В) или тока (1А) и рассчитывать ток или напряжение на выходе.

· Можно операторным методом. Аналогично рассчитывать ток или напряжение.

I₂(p) ¸>

U₂(p) ¸> с учетом что на входе U₁(p)= 1/p, потом u₂(t).

· Можно рассчитать через коэффициент передачи.

h (t) ¸ K(p)/p, h(t) = k(t), U₂(p) = K(p)·U₁(p).

Если найдем оригинал U₂(p) получим переходную характеристику.

· Применяя какие-либо программные средства.

· Экспериментальным путем (по осциллографу).

Импульсная характеристика.

· Классический метод не пригоден, т.к. воздействие бесконечно.

· Операторный метод использовать можно. Здесь изображение воздействия 1.

· Через К(р)

… F₁(p) / F₂(p) = K(p)

g(t) ¸ K(p) Удобно для стандартных цепей.

Программные средства

Через переходную характеристику. Импульсная функция является производной от единичной ступенчатой функции, соответственно и импульсная является производной переходной.

g(t) = h^/(t) + h (0)· δ(t), если h(0) не равна 0.

Экспериментально - не получится.

Пример нахождения временных характеристик

Определив коэффициенты A и B, получаем:

Тогда:

ω=2πf

Расчет откликов в электрической цепи на кусочно-непрерывное воздействие.

(Интеграллы Дюамеля и наложения)

При передаче информации сигналы могут быть сложными функциями, состоящими из отдельных скачкообразных воздействий.

В каждом интервале функция меняется по одному закону.

Разобьем функцию воздействия на элементарные ступеньки

Δτ→0 Δx=x^/ Δτ

Y(t) определяется с помощью переходной характеристики

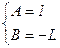
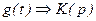
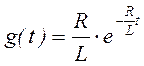
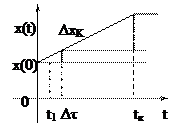
Это и есть интеграл Дюамеля