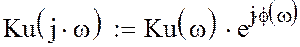Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет переходных процессов в сложных цепяхСодержание книги
Поиск на нашем сайте
Для решения цепи необходимо составить 3 ур: Ур по 1 закону Киргофа и 2ур по 2закону Киргофа i-iL-iC=0 uR+uL+uRK=E uC- uRK-uL=0 →Классический метод, где напрямую составляются дифференциальные уравнения громоздкий и трудоемкий для сложных цепей. Английский ученый Хевисайд предложил свой метод расчета переходных процессов. Этот метод получил название - операторный метод расчета. Здесь используется операционное исчисление на основе интегральных преобразований Лапласа, понятий оригинала, изображения и действий с ними. Преобразования Лапласса
Не должно быть скачков ∞ разрыва в оригинале. Допускаются конечные скачки. Найдем изображение единичной ступенчатой функции Хевисайда
Изображение от производной и интеграла по времени
Законы теории цепей в операторном виде От мгновенных токов и напряжений можно перейти к операторным и рассматривать основные законы в операторном виде, для так называемых операторных схем замещения, поскольку операции преобразования линейные. Рассмотрим схему с источником e(t)=1(t) сопротивлением, индуктивностью и параллельной ей емкостью
Закон Кирхгофа
Закон Кирхгофа. Эти законы можно записывать в операторной форме. Операторные схемы замещения реактивных элементов
Для индуктивности получим схему
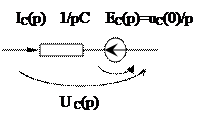
Для емкости получим
Для предыдущей схемы при нулевых начальных условиях получим
Нахождение функции времени в операторном методе Технически это значит нахождение откликов или реакций электрической цепи при каких-то коммутациях, т.е. зависимости токов или напряжений в электрических цепях. В общем это математическая процедура нахождения оригинала по операторному изображению. Теоретически можно выделить три способа нахождения: · по обратному преобразованию Лапласа.
· табличным способом. Подгонка операторного изображения под какие-то стандартные табличные функции.
· применение теоремы разложения Хевисайда. При определении операторных токов и напряжений в RLC -цепях можно увидеть, что они представляют собой дробно-рациональные функции сложного вида.
Хевисайдом была разработана теорема разложения сложной функции на простые с последующим определением оригинала, т.е. тока или напряжения, как функции времени. Т.е. Такую функцию можно разложить на элементарные дроби следующим образом:
Тогда оригинал легко ищется в виде суммы экспонент: Если один из корней равен 0, то Рассмотрим пример:
Корни могут быть комплексно-сопряженными. В этом случае пользуются общей формулой, причем
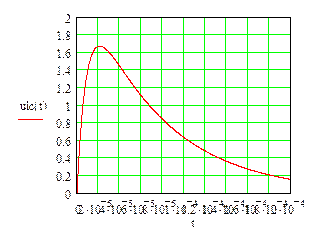
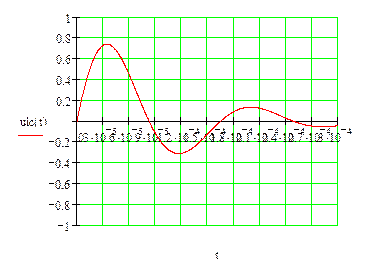
Для цепи с Ri и параллельными LC получиться при
R=500 Ом R=3000 Ом
Существует еще четвертый способ нахождения оригинала применением программных средств (Например: MathCad). Операторные передаточные функции
Операторная передаточная функция - это отношение операторного изображения реакции или отклика электрической цепи к операторному изображению воздействия на электрическую цепь. Приминается в основном для линейных цепей при нулевых независимых начальных условиях. Техническое название - операторные коэффициенты передачи. В зависимости от вида воздействия и типа реакции различают четыре варианта коэффициентов передач: · по напряжению U · по току I · по сопротивлению Z · по проводимости. Y КU(p) = ТU(p) = НU(p) = UВЫХ (2)(p)/UВХ(1)(p) КZ(p) = U2(p)/I1(p) КY(p) = I2(p)/U1(p) В линейных цепях передаточные функции не зависят от воздействия, а определяются только самой электрической цепью. (Бывают передаточные функции не электрического вида). Передаточные операторные функции являются обобщенными характеристиками электрической цепи. В частном случае они переходят в комплексные частотные характеристики (КЧХ). КЧХ®р=j·ω
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1085; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 f(t) – оригинал F(p)- изображение p комплексная переменная
f(t) – оригинал F(p)- изображение p комплексная переменная 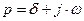 Оригинал должен возрастать не быстрее экспоненты.
Оригинал должен возрастать не быстрее экспоненты.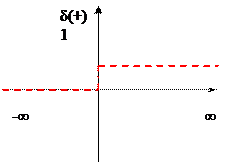
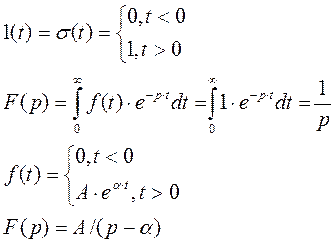
 Используя эти свойства можно от интегральных и дифференциальных уравнений перейти к алгебраическим.
Используя эти свойства можно от интегральных и дифференциальных уравнений перейти к алгебраическим.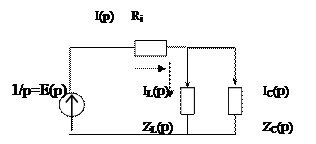

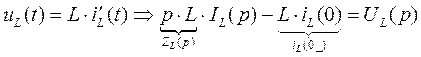

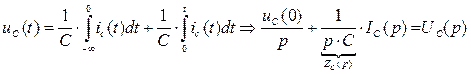
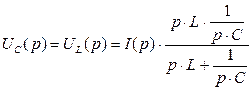 ,
, 
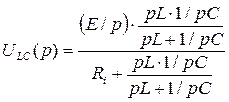
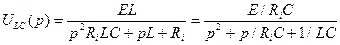

 D <0 при
D <0 при 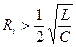


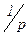
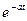
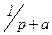
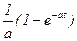
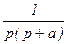

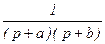
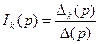
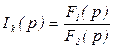 , где F1(p) – полином числителя, F2(p) – полином знаменателя.
, где F1(p) – полином числителя, F2(p) – полином знаменателя. . Здесь рК - корни знаменателя F2(p).
. Здесь рК - корни знаменателя F2(p).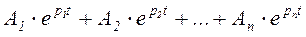 . Причем коэффициенты
. Причем коэффициенты 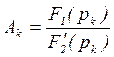 . Разложение возможно, если старшая степень числителя меньше степени знаменателя.
. Разложение возможно, если старшая степень числителя меньше степени знаменателя.

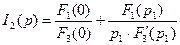
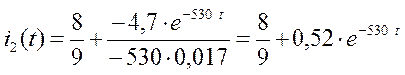
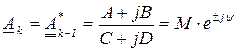
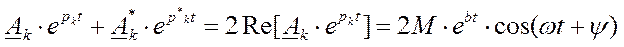 , если
, если 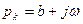
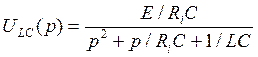
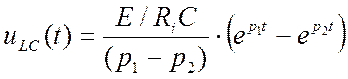
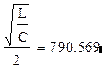 RКР
RКР