Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет цепей на постоянном токеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для расчета электрической цепи необходимо иметь расчетно-эквивалентную электрическую схему. Для составления такой схемы изучается реальная электрическая цепь. Рассмотрим детали таких цепей. Для каждой детали применяется схема замещения (модель), а затем составляется общая схема.
Здесь действует источник постоянной ЭДС, поэтому индуктивность не оказывает сопротивление (считается перемычкой), а емкость не пропускает ток (считается обрывом) и тогда RОБЩ =Rвн+R1+Rк+R2, I=E/RОБЩ , где E - электродвижущая сила ЭДС.
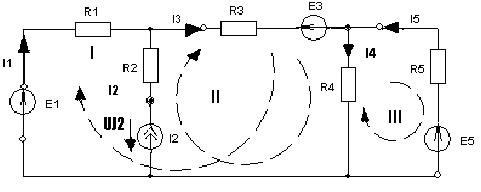
R34=R3+R4 Расчет цепей с несколькими источниками Рассмотрим расчетную электрическую схему цепи
Для проведения расчета сложной цепи используют законы Кирхгофа. В схеме сложной цепи применяют топологические или структурные понятия и параметры: · ветвь и количество ветвей; · узел и их количество; · контур и их количество. Ветвь - это участок электрической цепи, где протекает свой, не разветвляющийся электрический ток. В нашем случае NВ=NI=5. Узел - это точка, соединения трех и более ветвей (элементов) электрической цепи. В нашей цепи NУЗ=3. Узел может быть многоточечным – это когда между точками нет никаких элементов (3 узел). Контур - это замкнутый путь, проходящий однократно по ветвям и узлам электрической цепи или схемы в явном и неявном виде. Количество независимых контуров - это такая совокупность контуров, где каждый отличается от других каким-либо элементом. Причем все элементы должны войти в какой-то контур. NНК=NВ-NУЗ+1=NРЗЯ . Для нашей цепи NНК =3. В ряде случаев не учитываются контуры с ИИТ, тогда NНК =NВ-NУЗ+1- NJ и тогда =2. Законы Кирхгофа Законы Кирхгофа - это физические законы балансов токов в узлах и балансов напряжений в контурах цепи (моделях, схемах замещения). Первый закон Кирхгофа: Алгебраическая сумма мгновенных значений токов узла равна нулю в любой момент времени. Правило знаков: токи, направленные к узлу берутся с одним знаком, а от узла с противоположным.
Количество независимых уравнений определяется из условия N 13К(НУ)= N УЗ -1=2. Иногда используют другую формулировку первого закона Кирхгофа: Сумма подходящих к узлу токов равна сумме отходящих. Второй закон (правило) Кирхгофа: Алгебраическая сумма мгновенных значений напряжений на элементах контура равна нулю в любой момент времени. Напряжения, совпадающие с обходом контура, берутся со знаком «+», а не совпадающие со знаком «─».
Другая формулировка (рабочая) -алгебраическая сумма напряжений в контуре равна алгебраической сумме ЭДС в этом контуре. Из этих двух правил, мы можем составить систему уравнений для нашей цепи: 1 узел +I1+I2-I3=0 2 узел I3-I4+I5=0 3 узел -I1-I2+I4-I5=0 (не используется) Iконтур: -UE1+UR1+UJ2-UR2=0, UE1=Е1 IIконтур: UR2-UJ2+UR3+UR4=E3 IIIконтур: -UR4-UR5=-E5 Все напряжения расписываются по формуле UR=I∙R кроме напряжения на источнике тока UJ2. Получаем систему из пяти уравнений с пятью неизвестными.
I1 –I3= – J2 I3 –I4+I5=0 I1∙R1+UJ2 =E1 +J2∙R2 – UJ2+I3∙R3+I4∙R4=E3 – J2∙R2 – I4∙R4 – I5∙R5= – E5. Здесь четыре неизвестных токов (I1,3,4,5), одно напряжение (Uj2) и все известные величины перенесены в правую часть. Метод токов ветвей (МТВ) МТВ основан на непосредственном применении законов Кирхгофа к электрической цепи, приводит к решению системы уравнений. Применяется для сложной цепи, особенно если нельзя определить эквивалентное сопротивление цепи или в цепи действует несколько источников. В качестве основных неизвестных в МТВ используют токи ветвей. В качестве дополнительных неизвестных рассматривают напряжения на идеальных источниках тока. Начинают с определения структурных параметров (количество узлов, независимых контуров, ветвей). По первому закону Кирхгофа составляется (NУЗ-1) уравнений. По второму закону составляется столько уравнений, сколько независимых контуров в цепи NНК. Причем эти уравнения целесообразно разделить на основные и дополнительные. Поэтому соответственно контуры разделяют на основные и дополнительные. В основные контуры не должны входить идеальные источники тока. Каждый дополнительный контур должен содержать по одному идеальному источнику тока. Дополнительные уравнения, содержащие напряжения на источниках тока, не включают в систему уравнений, а записывают отдельно. Рассмотрим на примере.
Nуз=3, NуIзк=2, Nнк=3, NуIIзк=3, Nосн.ур.=2 (2 контура без ИИТ, Nдоп.ур.=1(1 ИИТ). Число неизвестных токов здесь 4 (I1, I3, I4 ,I5)
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |



 .
.
 , где ik(t) - мгновенное значение силы тока, а аk - множитель (-1; 1; 0).
, где ik(t) - мгновенное значение силы тока, а аk - множитель (-1; 1; 0). аk - множитель (-1; 1; 0).
аk - множитель (-1; 1; 0).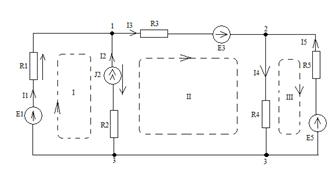 Напряжения на резисторах выражаются через токи, следовательно, имеем систему уравнений с неизвестными токами и неизвестными напряжениями на источниках тока, которая решается математическими приемами.
Напряжения на резисторах выражаются через токи, следовательно, имеем систему уравнений с неизвестными токами и неизвестными напряжениями на источниках тока, которая решается математическими приемами.