
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Под комплексной передаточной функцией понимают отношение комплексного изображения гармонической реакции лэц к комплексному изображению гармонического воздействия на цепь.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть воздействие
Сокращенно функцию T(jω) называют комплексным коэффициентом передачи. Модуль комплексного коэффициента T(ω) представляет собой амплитудно-частотную характеристику (АЧХ). Аргумент комплексного коэффициента передачи АЧХ – это такая характеристика цепи, которая показывает, как изменяется в зависимости от частоты отношение амплитуды реакции (выходного сигнала) к амплитуде воздействия (входного сигнала) при гармоническом воздействии. ФЧХ – это такая характеристика цепи, которая показывает, как изменяется сдвиг фаз выходного и входного сигнала в зависимости от частоты при гармоническом воздействии. Это основные характеристики электрических цепей. Теоретически они рассчитываются с помощью расчетных методов на основе законов Ома и Кирхгофа в комплексной форме. Практически они измеряются с использованием приборов (вольтметров, фазометров, осциллографов). В зависимости от вида реакции и воздействия различают четыре типа передаточных функций: по напряжению (напряжение / напряжение), по току (ток / ток), по сопротивлению (напряжение / ток), по проводимости (ток /напряжение). Для примера рассмотрим колебательный контур:

кривая пунктирная при Q<1, при ω=ω0 К0=Q
С использованием расстройки Влияние внешнего сопротивления на избирательность контура К внешним сопротивлениям относятся сопротивления источника сигнала и нагрузки. В идеале
При той же частоте при меньшей добротности меньше коэффициент подавления помехи, так как обобщенная расстройка пропорциональна добротности. Нужно иметь источник с малым внутренним сопротивлением, катушку индуктивности с малыми потерями (толстым проводом или из дорогих материалов) и нагрузку с большим сопротивлением, тогда будет больше подавляться помеха на при той же расстройке. Параллельный колебательный контур (простой)
Полоса пропускания П определяется аналогично, как для последовательного контура по уровню половинной активной мощности. Коэффициент подавления помехи:
Схема замещения:
Условие резонанса: Условие приближения к идеальному контуру: Резонансное сопротивление:
Векторная диаграмма:
Частотные зависимости параллельного контура

Если действует гармонический ток на контур, то при значении I(m)=const действующее напряжение на контуре и амплитудное будет повторять зависимостьвеличины Z от w
П= ω2 – ω1 (f2 – f1) Здесь полоса пропускания определяется по уровню 0,707 от максимального значения напряжения на контуре и обобщенная расстройка на границах равна +,- 1.
При резонансе (x=0) Х=0. Зависимость Х от x показана ниже. Параллельный колебательный контур на частоте ниже резонансной (x<0) ведет себя как некоторая индуктивность (Х>0), на частоте выше резонансной (x>0) – некоторая емкость (Х<0).
Здесь X(Э)=Im(Z).
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 852; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , а реакция
, а реакция  ; а комплексная передаточная функция
; а комплексная передаточная функция  . Тогда
. Тогда  . Если воздействие гармоническое и мы будем менять частоту, то получим комплексную частотную характеристику (КЧХ).
. Если воздействие гармоническое и мы будем менять частоту, то получим комплексную частотную характеристику (КЧХ).
 - это фазово-частотная характеристика (ФЧХ).
- это фазово-частотная характеристика (ФЧХ).


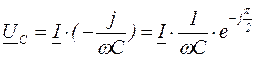




 и влияния нет. В противном случае они влияют на добротность контура, уменьшая ее и, соответственно, ухудшая избирательность. Эквивалентная добротность с учетом нагрузки может быть рассчитана
и влияния нет. В противном случае они влияют на добротность контура, уменьшая ее и, соответственно, ухудшая избирательность. Эквивалентная добротность с учетом нагрузки может быть рассчитана . С учетом сопротивления источника
. С учетом сопротивления источника - итоговая.
- итоговая. 1. Идеализированный контур
1. Идеализированный контур - комплексная проводимость.
- комплексная проводимость. - резонансная частота
- резонансная частота 
 - характеристическое сопротивление, сопротивление реактивного элемента на резонансной частоте,
- характеристическое сопротивление, сопротивление реактивного элемента на резонансной частоте, , - усилительная способность контура где IL0, IC0 – токи при резонансной частоте; I – общий ток.
, - усилительная способность контура где IL0, IC0 – токи при резонансной частоте; I – общий ток.  ,
,  . При резонансе емкостной ток компенсируется индуктивным и поэтому резонанс в параллельном контуре называется резонансом токов.
. При резонансе емкостной ток компенсируется индуктивным и поэтому резонанс в параллельном контуре называется резонансом токов. Рассчитаем токи в ветвях идеального параллельного контура при резонансе. При резонансе (w=w0(Р)) токи в ветвях контура равны
Рассчитаем токи в ветвях идеального параллельного контура при резонансе. При резонансе (w=w0(Р)) токи в ветвях контура равны

 2. Реальный параллельный контур - это цепь из параллельно соединенных конденсатора и катушки индуктивности.
2. Реальный параллельный контур - это цепь из параллельно соединенных конденсатора и катушки индуктивности.
 ,
, 

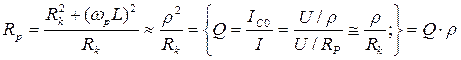





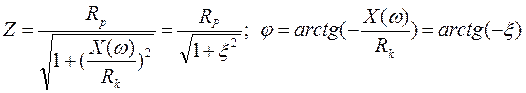








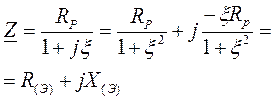
 , R(Э)=Re(Z),
, R(Э)=Re(Z),



