
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выделяют нелинейное резистивное сопротивление, нелинейную индуктивность и нелинейную емкость и электронные компоненты.Содержание книги
Поиск на нашем сайте
Зависимость напряжения от тока в нелинейном элементе называют вольт- амперной характеристикой (ВАХ). Ее можно записать с помощью полинома (аппроксимировать).
Нелинейное резистивное сопротивление характеризуют: 1) статическим сопротивлением в некоторой точке ВАХ где U о — приложенное к НЭ постоянное напряжение; I о — протекающий через НЭ постоянный ток. Это сопротивление постоянному току; оно характеризуется тангенсом угла наклона прямой, проходящей через начало координат и рабочую току (U о, I о) на ВАХ НЭ. В силу предположения о резистивном характере цепи статические характеристики определяют одновременно и соотношения между мгновенными значениями напряжений и токов на внешних зажимах соответствующего нелинейного прибора. Дифференциальным сопротивлением Определим дифференциальное сопротивление RД как отношение приращения напряжения ∆ и к приращению тока ∆ i под воздействием переменного напряжения малой амплитуды при некотором смещении рабочей точки на ВАХ: R Д = ∆ u/∆ i. Это сопротивление представляет собой сопротивление НЭ переменному току малой амплитуды. Обычно переходят к пределу этих приращений и определяют дифференциальное сопротивление в виде R Д = d u/d i. Оно характеризуется тангенсом угла наклона касательной к ВАХ в рабочей точке (U о, I о). Иногда удобно пользоваться понятием дифференциальной крутизны (имеющей смысл проводимости) S Д = G Д = 1/R Д = di/ du. Аналогичные исследования проводятся для нелинейной индуктивности и емкости. Расчет простейших нелинейных резистивных цепей Последовательное соединение
При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ Применение указанной методики иллюстрируют графические построения на приведенных выше рисунках. Параллельное соединение При параллельном соединении нелинейных резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам и строится итоговая ВАХ путем сложения токов резисторов при одинаковых напряжениях.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 645; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.19 (0.005 с.) |

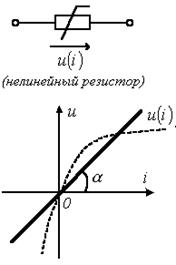 Рассмотрим нелинейные резисторы, обозначение которых содержит ломанную линию, а пример нелинейной зависимости между напряжением и током показан пунктирной линией. Могут быть резисторы R=R(i) – управляемые током; R=R(u) – управляемые напряжением.
Рассмотрим нелинейные резисторы, обозначение которых содержит ломанную линию, а пример нелинейной зависимости между напряжением и током показан пунктирной линией. Могут быть резисторы R=R(i) – управляемые током; R=R(u) – управляемые напряжением. - аппроксимация – подбор функции, которая соответствует данному графическому изображению.
- аппроксимация – подбор функции, которая соответствует данному графическому изображению. Статическое сопротивление R СТопределяется как R СТ =U о /I о
Статическое сопротивление R СТопределяется как R СТ =U о /I о 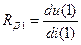 > <0
> <0
 отдельных резисторов в системе декартовых координат
отдельных резисторов в системе декартовых координат  строится результирующая зависимость
строится результирующая зависимость  путем сложения напряжений на отдельных резисторах при одинаковых токах.. Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью
путем сложения напряжений на отдельных резисторах при одинаковых токах.. Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью  . Из точки пересечения перпендикуляра с кривой
. Из точки пересечения перпендикуляра с кривой 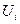 на отдельных резистивных элементах.
на отдельных резистивных элементах. . Далее на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ
. Далее на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ  ), из которой восстанавливается перпендикуляр до пересечения с зависимостью
), из которой восстанавливается перпендикуляр до пересечения с зависимостью  . Из точки пересечения перпендикуляра с кривой
. Из точки пересечения перпендикуляра с кривой  в ветвях с отдельными резистивными элементами.
в ветвях с отдельными резистивными элементами.


