
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим простейший способ: метод выбранных точек или узлов интерполяции степенным полиномом.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимо определить коэффициенты полинома. Для этого выбирается (n+1) точек на заданной функции и составляется система уравнений:
Из этой системы находятся коэффициенты а0, а1, а2, …, аn. В выбранных точках аппроксимирующая функция будет совпадать с исходной, в других точках – отличаться (сильно или нет – зависит от степенного полинома). Можно использовать экспоненциальный полином:
Второй метод: метод аппроксимации по Тейлору. В этом случае выбирается одна точка, где будет совпадение исходной функции с аппроксимирующей, но дополнительно ставится условие, чтобы в этой точке совпадали еще и производные. Аппроксимация по Батерворту: выбирается простейший полином: В этом случае можно определить максимальное отклонение ε на краях диапазона.
f (x) - ξ(х) не меньше, чем п + 2 раза принимает свои последовательно чередующиеся предельные наибольшие f (x) - ξ(х) = L > 0 и наименьшие f (x) - ξ(х) = -L значения (критерий Чебышева). Во многих прикладных задачах находит применение полиномиальная аппроксимация по среднеквадратическому критерию близости, когда параметры аппроксимирующей функции f (x) выбираются из условия обращения в минимум в интервале аппроксимации а ≤ х ≤ b квадрата отклонения функции f (x) от заданной непрерывной функции ξ(х), т. е., из условия: b Λ= 1/b-a∫a [ f (x) - ξ(x)]2 dx = min. (7) В соответствии с правилами отыскания экстремумов решение задачи сводится к решению системы линейных уравнении, которая образуется в результате приравнивания к нулю первых частных производных функции Λ по каждому из искомых коэффициентов ak аппроксимирующего полинома f (x), т. е. уравнений дΛ ∕дa0 =0; дΛ ∕дa1 =0; дΛ ∕дa2 =0,..., дΛ ∕дan =0. (8) Доказано, что и эта система уравнений имеет единственное решение. В простейших случаях оно находится аналитически, а в общем случае — численно.
Чебышев установил, что должно для максимальных отклонений выполняться равенство:
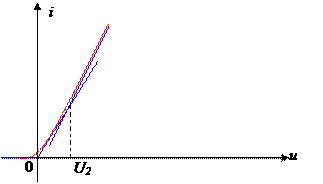
В инженерной практике используется еще так называемая кусочно-линейная аппроксимация – это описание заданной кривой отрезками прямых линий.
В пределах каждого из линиаризированных участков вольт - амперной характеристики применимы все методы анализа колебаний в линейных электрических цепях. Ясно, что, чем на большее число линеаризированных участков разбивается заданная вольт-амперная характеристика, тем точнее она может быть аппроксимирована и тем больше объем вычислений в ходе анализа колебаний в цепи. Во многих прикладных задачах анализа колебаний в нелинейных резистивных цепях аппроксимируемая вольт - амперная характеристика в интервале аппроксимации с достаточной точностью представляется двумя или тремя отрезками прямых. Подобная аппроксимация вольт - амперных характеристик дает в большинстве случаев вполне удовлетворительные по точности результаты анализа колебаний в нелинейной резистивной цепи при «небольших» по величине воздействиях на нелинейный элемент, т. е. когда мгновенные значения токов в нелинейном элементе изменяются в предельно допустимых границах от I = 0 до I = Iмах Определение реакции нелинейного элемента на гармоническое Воздействие 1. Гармоническое воздействие малой амплитуд c постоянной составляющей
В этом случае можно отдельно рассмотреть реакцию на постоянную составляющую и на гармоническое воздействие. Здесь можно использовать понятие статического и дифференциальных сопротивлений в рабочей точке ВАХ (U0), а также графический метод на линейном участке.


Большая амплитуда напряжения Используется графический метод (строится реакция путем переноса точек на нелинейном участке).

|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.7.226 (0.009 с.) |



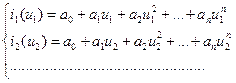
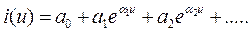


 Аппроксимация по Чебышеву: является степенной, там устанавливается совпадение в нескольких точках и минимизируется максимальное отклонение аппроксимирующей функции от исходной. В теории аппроксимации функций доказывается, что наибольшее по абсолютной величине отклонение полинома f (x)степени п от непрерывной функции ξ(х) будет минимально возможным, если в интервале приближения а ≤ х ≤ b разность
Аппроксимация по Чебышеву: является степенной, там устанавливается совпадение в нескольких точках и минимизируется максимальное отклонение аппроксимирующей функции от исходной. В теории аппроксимации функций доказывается, что наибольшее по абсолютной величине отклонение полинома f (x)степени п от непрерывной функции ξ(х) будет минимально возможным, если в интервале приближения а ≤ х ≤ b разность
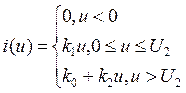
 , где
, где  - постоянная составляющая,
- постоянная составляющая, 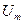 - амплитуда малой величины.
- амплитуда малой величины. , где
, где  ,
, 



