
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Емкостное сопротивление обратно пропорционально частотеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
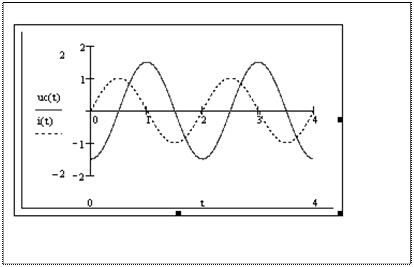
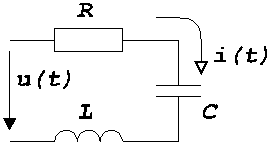
Емкостное напряжение отстает от тока по фазе на четверть периода (900) Анализ последовательной RLC -цепи при гармоническом воздействии
На основе второго закона Кирхгофа u = uR+uC +uL или в комплексной форме U = U R + U C + U L . С учетом
где Преобразовав, получаем, что где Запишем закон Ома в комплексной форме с учетом фазовых соотношений
Треугольник сопротивлений в RLC – цепи.
Рассмотрим зависимости полного сопротивления Z и угла сдвига фаз φ в последовательной RLC -цепи от частоты. На некоторой частоте ω0может выполняться равенство


ω0 До частоты ω0 напряжение отстает от тока, после ω0 напряжение опережает ток. Рассмотрим зависимость тока и напряжения на резисторе от частоты 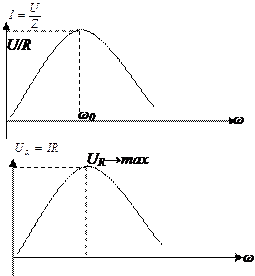
Рассмотрим напряжения на индуктивности и емкости
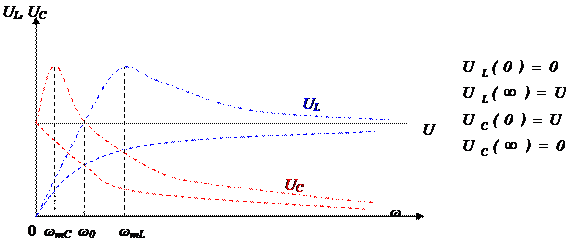
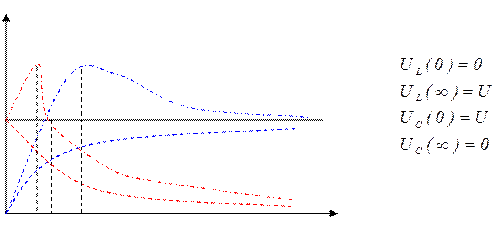
Варианты графиков UL. UC в RLC – цепи. Графики могут иметь максимумы, а могут и не иметь (это зависит от соотношения величин элементов).
Векторные диаграммы последовательной RLC -цепи Совокупность нескольких векторов, отображающих токи и напряжения в некоторой цепи, называется векторной диаграммой. Для последовательной RLC – цепи диаграмму строят, откладывая по горизонтали ток, затем также по направлению тока откладывают в масштабе вектор резистивного напряжения, потом из его конца откладывают перпендикулярно вверх вектор индуктивного напряжения и из его конца вниз вектор емкостного. Вид диаграмм зависит от выбранной частоты по отношению к резонансной. 1) ω<ω0, UL < UC
2) ω=ω0 → UL=UC φ=0
Параллельные RLC - цепи
U = I · Z = I / Y
Все ее элементы соединены параллельно и находятся под одним и тем же напряжением u(t)=Um▪sin(wt+yu). Необходимо определить ток в цепи i(t). На основании 1-го закона Кирхгофа в любой момент времени справедливо соотношение
на какой-то частоте ω0, которую называют резонансной.
Закон Ома в комплексной форме для цепи записывается Отсюда следует, что при параллельном соединении ветвей цепи комплексная эквивалентная проводимость равна сумме комплексных проводимостей ветвей:
Напряжение взято как опорный вектор, ток в резисторе совпадает по фазе с напряжением, ток в индуктивности отстает на 900, а ток емкостной опережает на 900 и меньше (ω<ω0). Общий ток равен сумме векторов всех токов и он отстает от напряжения по фазе. Принцип дуальности в электрических цепях В электрических цепях есть некоторые понятия, которые с одной стороны противоположны друг другу, а с другой стороны взаимосвязаны и дополняют друг друга (из физики: электромагнитное поле - электрическое поле и магнитное поле). Такие понятия, величины называются дуальными. У дуальных величин формы записи и математические уравнения одинаковы. Напряжение ток Контур узел Закон Кирхгофа 2 закон Кирхгофа Сопротивление проводимость U = I · ZI = U · Y L C
Последовательная цепь параллельная цепь ИИН ИИТ Формулы, полученные для некоторой цепи можно формально распространить на дуальные величины в дуальной цепи. Дуальные величины ведут себя одинаково в дуальных цепях, а такие же будут вести себя противоположно в тех же условиях. Пример 2 Здесь Е1- источник постоянной эдс, а j2 – источник переменного тока
В данном случае мы можем использовать только метод наложения. Составим две схемы замещения, в первой из которых рассчитываются частичные токи от источника постоянной эдс. Поэтому в ней индуктивность заменена перемычкой, а емкость – разрывом. Во второй схеме рассчитываются частичные токи от источника переменного тока и здесь необходимо перевести все токи, напряжения и сопротивления в комплексную форму и записать законы Кирхгофа в комплексной форме.
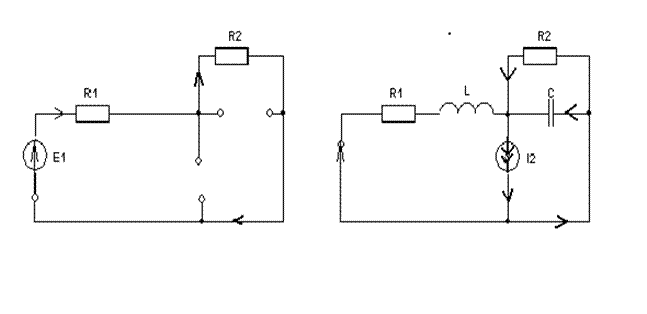
I1E1=E1/(R1+R2)=I2E1=I3E1. Тут надо составлять уравнения по МКТ в комплексной форме. Например, по 1 закону I 1J2+ I R2J2+ I CJ2 –J2=0, - I CJ2 - I R2J2+ I 3J2=0. Можно использовать и общую проводимость относительно источника тока. В итоге получается, что i1=I1E1+i1 j2, iR2=IR2E1 – iR2j2, ic=icj2, i3=I3E1 – i3j2, i2=j2.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1825; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

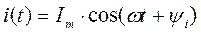
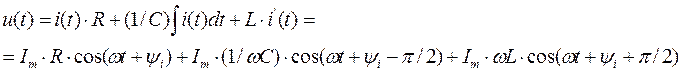
 получим
получим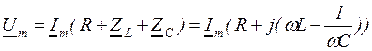
 - комплексное сопротивление RLC - цепи
- комплексное сопротивление RLC - цепи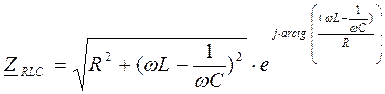 ,
,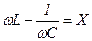 - реактивное сопротивление,
- реактивное сопротивление, 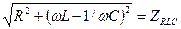
 - полное сопротивление цепи, а
- полное сопротивление цепи, а 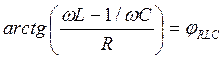 - угол сдвига фаз RLC цепи.
- угол сдвига фаз RLC цепи.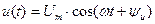 :
: . Здесь
. Здесь  .
.
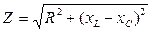 - полное сопротивление RLC - цепи,
- полное сопротивление RLC - цепи, угол сдвига фаз RLC - цепи.
угол сдвига фаз RLC - цепи.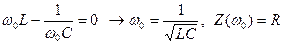
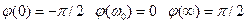
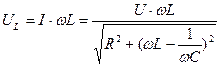 ;
; 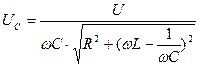
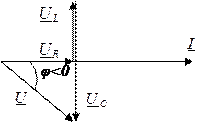
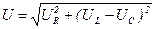

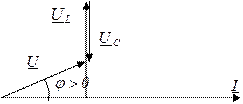 3) ω>ω0. UL > UC
3) ω>ω0. UL > UC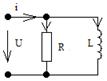
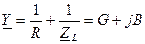 Y – комплексная проводимость, B – реактивная Рассмотрим схему с параллельными RLC - элементами:
Y – комплексная проводимость, B – реактивная Рассмотрим схему с параллельными RLC - элементами: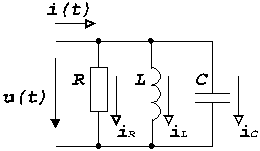
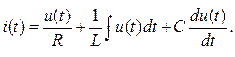
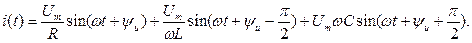
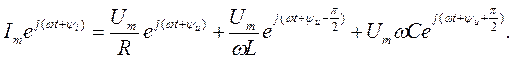
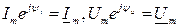 , получим
, получим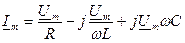

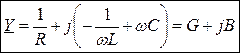 ,
, 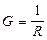 – резистивная составляющая проводимости,
– резистивная составляющая проводимости, – реактивная составляющая проводимости. и она может быть равна 0
– реактивная составляющая проводимости. и она может быть равна 0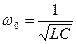

 или
или
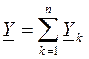 Проанализируем векторную диаграмму параллельной RLC - цепи
Проанализируем векторную диаграмму параллельной RLC - цепи
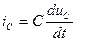
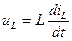
 .
.
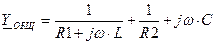 ,
, 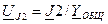 ,
, 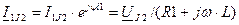 ,
, 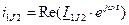 . Аналогично остальные токи
. Аналогично остальные токи


