
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найдем комплексную спектральную плотность одиночного прямоугольного импульса при симметричном расположении.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Uu

Получается непрерывная функция частоты вида
Вывод: Спектр одиночного сигнала похож на спектр последовательности таких же сигналов, точнее соответствует огибающей спектра дискретного сигнала, но размерности у них разные. Математически спектральная плотность симметричная функция
Рассмотрим несимметричное расположение сигнала. Найдем его спектр. Это можно сделать напрямую с помощью интеграла Фурье, а можно по теореме запаздывания.  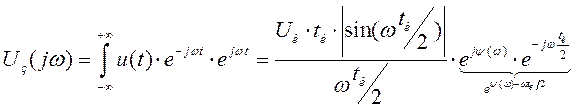
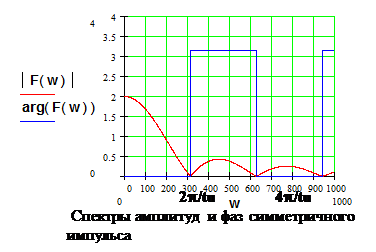
Общий угол Ψ(ω)-ωtu/2 Спектральная плотность амплитуд не изменяется,
Спектры некоторых типовых сигналов Их можно получить на основе прямого преобразования Фурье, а можно из операторных изображений этих сигналов, заменив p на jω. 1) Единичная ступенчатая функция: 2) Единичная импульсная функция Экспонента: 3) Профессиональный сигнал – радиоимпульс
Определим спектр такого сигнала. Это можно сделать, используя теорему смещения в области комплексного переменного.
Спектр импульса переносится в район частоты – ωЗ и ωЗ. При частоте 1000 р/c получим На этом принципе работают все радиостанции, передающие радиосигналы. Понятие об энергетическом спектре одиночных сигналов. Ширина спектра Энергия сигналов зависит от мощности, поэтому рассматривают мощность электрического сигнала, при этом выбирают единичное сопротивление для того, чтобы были стандартные условия. Следовательно, мощность и энергия пропорциональны квадрату рассматриваемой величины сигнала (тока или напряжения). Полная энергия сигнала может быть найдена как:
Поскольку частота и время – независимые переменные, то порядок интегрирования можно менять местами. Квадрат модуля спектральной плотности называют энергетическим спектром сигнала. В энергии большие составляющие играют более важную роль, чем в форме сигнала. Под шириной спектра для одиночного сигнала понимают диапазон частот, где сосредоточена основная доля энергии сигнала (90%). Ширину спектра можно определить, решая интегральное уравнение:

Более точно получается при использовании площади (можно рассчитать всю площадь по клеточкам, потом рассчитать ее десятую часть и отнять от полной мощности графически).
Условия безыскаженной передачи электрических сигналов В системах передачи информации электрические цепи в основном предназначены для передачи электрических сигналов, несущих какую-то информацию. При этом желательно, чтобы информация не изменялась; для этого электрический сигнал не должен меняться или искажаться (какой был на входе, такой должен оставаться на выходе). Допускается масштабное изменение сигнал по величине и незначительное для земных условий запаздывание во времени.
Определим требования к коэффициенту передачи K(jω), чтобы не было искажений.
Для неискажающей цепи АЧХ должна быть постоянной на всех частотах, а ФЧХ должна быть линейной функцией от частоты. Если АЧХ – постоянная, то соотношение между амплитудами спектральных составляющих остается неизменным. Если время запаздывания t3 для всех составляющих одинаково, то они одинаково запаздывают т.к. t3 является производной от ФЧХ, а для линейной оно постоянно. Графически это можно изобразить следующим образом: Практически таких характеристик не бывает. Реально нет цепей без искажения сигнала, можно передавать сигналы с некоторыми минимальными искажениями.
Третье требование – не должно быть отражения сигнала или «эха».
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 840; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.45 (0.008 с.) |




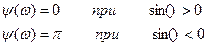





 . Следовательно, спектральная плотность амплитуд равна
. Следовательно, спектральная плотность амплитуд равна  .
. . Спектральная плотность равна 1, т.е. спектральная плотность равномерна.
. Спектральная плотность равна 1, т.е. спектральная плотность равномерна.

 Радиоимпульс ─ сигнал, огибающая которого соответствует прямоугольному импульсу, но он имеет заполнение какой-то частотой ωЗ . Частота заполнения ─ технически частота несущей радиостанции.
Радиоимпульс ─ сигнал, огибающая которого соответствует прямоугольному импульсу, но он имеет заполнение какой-то частотой ωЗ . Частота заполнения ─ технически частота несущей радиостанции.


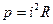 =u2/R
=u2/R - на единичном сопротивлении.
- на единичном сопротивлении. 

 Простейшим способом определения граничной частоты ширины спектра является графический: строится график и определяется частота, при которой значения энергетического спектра становятся меньше 0,1 от максимального.
Простейшим способом определения граничной частоты ширины спектра является графический: строится график и определяется частота, при которой значения энергетического спектра становятся меньше 0,1 от максимального.






