
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импульсная и частотная характеристика оптимального фильтраСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Известно, что импульсная характеристика линейной цепи и её частотная передаточная характеристика связаны парой преобразований Фурье:
Подставляя
С другой стороны, спектральная плотность сигнала равна: Следовательно, должно выполняться равенство: Модуль передаточной характеристики фильтра пропорционален модулю спектральной характеристики сигнала Рассмотрим АЧХ и ФЧХ оптимального фильтра для прямоугольного видеоимпульса
Рис. 1 а, б Пусть на выходе оптимального фильтра действует сумма сигнала с белым шумом:
сигнал характеризуется спектральной плотностью
а спектральная плотность мощности шума на выходе будет равна
Отсюда следует, что шум имеет на выходе спектральную плотность мощности, подобную спектральной плотности амплитуд самого сигнала. На рис.2 показаны спектральная плотность сигнала (а) и спектральная плотность шума (б) на выходе оптимального фильтра для видеоимпульса длительностью.
Рис. 2 Ослабление по краям выражается для шума сильнее, чем для сигнала. В результате шум ослабляется в целом сильнее, чем сигнал, Кроме того, благодаря ФЧХ фильтра, все спектральные составляющие сигнала на выходе фильтра в момент t = t0 имеют одну и ту же нулевую фазу. Таким образом, схема обнаружителя сигнала со случайной фазой имеет вид (рис.3).
ВОПРОС №21 Эффективная площадь рассеяния цели (ЭПР)
где
откуда получаем общее выражение для ЭПР
Плотность потока мощности на расстоянии
Это произведение имеет размерность площади и характеризует, какую часть энергии падающей радиоволны получает цель, потери энергии во вторичном излучателе, направленные свойства вторичного излучения. Тогда, подставляя (1.4), (1.5), (1.6), (1.7) в (1.2), окончательно получим
где Из формулы (1.2), получаем общее выражение для ЭПР:
ВОПРОС №22
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 995; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

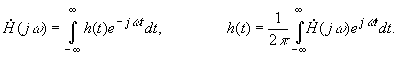
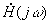 в требуемое выражение для
в требуемое выражение для 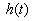 , имеем
, имеем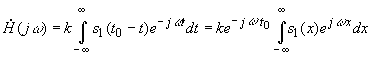
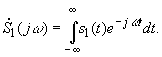
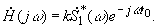
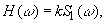 а его фаза
а его фаза 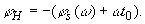
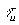 , спектральная плотность которого изображена на рис. 1, а, АЧХ оптимального фильтра с точностью до постоянного множителя повторяет форму АЧХ сигнала, а его ФЧХ повторяет ФЧХ сигнала с обратным знаком с учетом задержки (см. рис. 1, б).
, спектральная плотность которого изображена на рис. 1, а, АЧХ оптимального фильтра с точностью до постоянного множителя повторяет форму АЧХ сигнала, а его ФЧХ повторяет ФЧХ сигнала с обратным знаком с учетом задержки (см. рис. 1, б).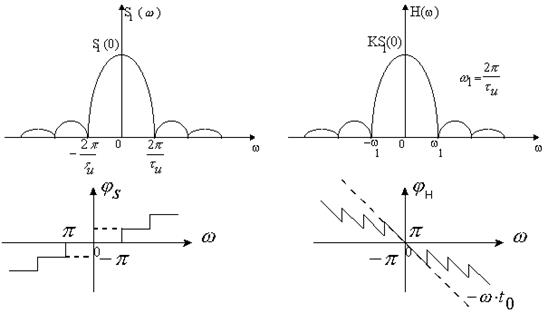
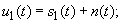
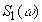 , а шум – спектральной плотностью мощности N0. Тогда на выходе фильтра имеем:
, а шум – спектральной плотностью мощности N0. Тогда на выходе фильтра имеем: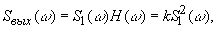
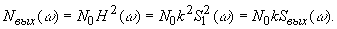
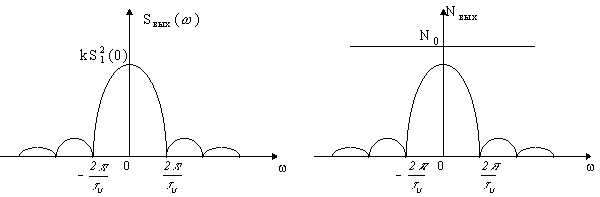

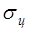 - площадь некоторой фиктивной плоской поверхности, положенной нормально к направлению падающей волны и являющейся идеальным и изотропным переизлучателем, которая, будучи помещена в точку цели, создает у антенны РЛС ту же плотность потока мощности, что и реальная цель. Из определения следует, что полностью переизлучаемая ЭПР мощность
- площадь некоторой фиктивной плоской поверхности, положенной нормально к направлению падающей волны и являющейся идеальным и изотропным переизлучателем, которая, будучи помещена в точку цели, создает у антенны РЛС ту же плотность потока мощности, что и реальная цель. Из определения следует, что полностью переизлучаемая ЭПР мощность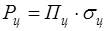 , (1.1)
, (1.1)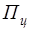 - плотность потока мощности падающей плоской волны у цели (т.е., мощность, приходящаяся на
- плотность потока мощности падающей плоской волны у цели (т.е., мощность, приходящаяся на 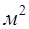 поверхности волнового фронта). Плотность потока мощности у РЛС
поверхности волнового фронта). Плотность потока мощности у РЛС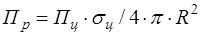 , (1.2)
, (1.2)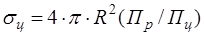 . (1.3)
. (1.3)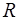 у РЛС с учетом же направленных свойств цели равна
у РЛС с учетом же направленных свойств цели равна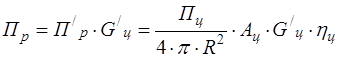 . (1.7)
. (1.7)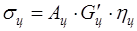 , (1.8)
, (1.8)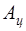 - характеризует геометрические свойства цели,
- характеризует геометрические свойства цели, 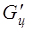 - свойство цели избирательно отражать энергию в определенных угловых направлениях (анизотропность). Так как величина
- свойство цели избирательно отражать энергию в определенных угловых направлениях (анизотропность). Так как величина 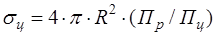 . (1.9)
. (1.9)


