Cтробирование и селекция отметок в стробах

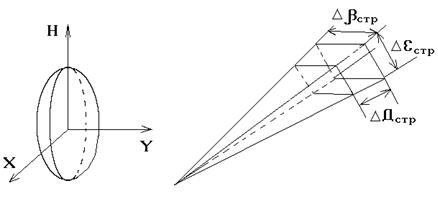
Одной из операций, выполняемых в процессе сопровождения целей, является выделение области, в которой с определенной вероятностью ожидается появление отметки в новом обзоре (стробирование).

Строб представляет собой заранее выбранную область зоны обзора РТС, координаты центра которой совпадают с координатами экстраполированных точек (ЭТ). Размер и форма строба выбираются так, чтобы вероятность попадания в него наблюдаемой отметки (НО), принадлежащей данной трассе была близка к единице.

В строб могут попасть и ложные отметки или отметки, принадлежащие другим траекториям. Поэтому возникает необходимость селекции отметок, попавших в строб, с целью выбора одной отметки, для которой вероятность принадлежности к сопровождаемой трассе является наибольшей. Селекция производится на основе сравнения координат и параметров новых отметок с экстраполированными координатами и характеристиками сопровождаемых трасс.

К числу сравниваемых параметров могут относиться данные о высоте цели, ее составе, признак государственной принадлежности и др. В простейшем случае селекция трасс производится только по координатам отметок.

Стробирование отметок может быть физическим или математическим.

Важной задачей в процессе стробирования отметок трассы является выбор формы и размеров стробов.

Для определения оптимальной формы стробов необходимо найти поверхность равновероятного отклонения НО от ЭТ.

а) б)

Рис. 2. Эллипсоидальный строб (а) и простейший строб (б)

Обычно форма строба выбирается простейшей для задания в той системе координат, в которой осуществляется обработка РЛИ. При обработке в сферической системе координат простейший строб задается линейным размером по дальности ΔД_стри двумя угловыми размерами: по азимуту Δβ_стр и по углу места Δε_стр (рис. 2,б).

Эти размеры установлены заранее, исходя из учета максимальных значений случайных и динамических ошибок по всем подлежащим обработке траекториям.

В качестве координат центра строба выбираются экстраполированные значения дальности Д_nэ, азимута β_nэ и угла места ε_nэ, рассчитанные на n -й обзор. Поэтому очередная отметка с координатами Д_n, β_n и ε_n считается попавшей в строб, если одновременно выполняются условия

| Д _n– Д _nэ| ≤ ΔД _стр/ 2; |β_n–β_nэ| ≤ Δβ_стр/ 2; |ε_n–ε_nэ| ≤ Δε_стр/ 2.

При обработке в прямоугольной системе координат x, y, H целесообразно выбрать строб в виде параллелепипеда с параметрами Δ х _стр, Δ у _стр, Δ Н _стр. Тогда условия попадания отметки в строб будет определяться неравенствами:

| x_n – x^*_nэ | ≤ Δ x _стр/ 2; | y_n – y^*_nэ | ≤ Δ y _стр/ 2; | H_n – H^*_nэ | ≤ Δ H _стр/ 2.

Селекция отметок в стробе.

В строб помимо истинной отметки могут попадать ложные отметки, образованные помехами, прошедшими фильтр первичной обработки, а также отметки траекторий других целей. Попадание ложных отметок в строб создает в нем неопределенную ситуацию, требующую дальнейшего анализа.

При анализе возможны два подхода:

1. Имея несколько отметок в стробе, продолжать траекторию по каждой из них. Траектории, продолженные по ложным отметкам, из-за отсутствия корреляции между последними в соседних обзорах будут через несколько обзоров сброшены, а траектории, продолженные по истинным отметкам, останутся.

2. Выбрать в стробе одну отметку, вероятность принадлежности которой к сопровождаемой траектории наибольшая, и по ней продолжать траекторию, а остальные отметки отбросить как ложные.

Оптимизация процесса селекции отметок по их отклонениям от центра строба производится по критерию максимального правдоподобия, в соответствии с которым за истинную отметку надо принимать ту, для которой функция правдоподобия максимальна.

Упрощением рассмотренного оптимального алгоритма является алгоритм селекции по минимуму суммы квадратов линейных отклонений координат отметки от центра строба.

 

ВОПРОС №24