
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суть фазового метода пеленгации.Содержание книги
Поиск на нашем сайте
1.3. Фазовые методы пеленгации
где e - угол падения электромагнитной волны на антенную систему из двух элементов (1 и 2). Эти колебания, отличаются по фазе на величину
Окончательно выражение для разности фаз сигналов с учетом и можно записать в следующем виде:
тогда: Разность фаз Dj может быть измерена с помощью фазометра ФД. Результат измерения считывается с устройства отображения УО. По разности фаз можно определить направление на источник излучения. С выхода ФД получим:
при малых углах места
из () видно, что однозначные показания пеленгатора eОДН получаются, если угол
Например, при l=3см, d = 5см, l/d=0.2 диапазон однозначного измерения угла составляет 11,50.Чем больше величина d, тем в меньшей мере погрешности оценивания фазы влияют на снижение качества пеленгации. Неоднозначность может быть устранена много шкальными методами с использованием дополнительных приемных антенн, расположенных в других точках, а также путем применения направленных антенн. В последнем случае ширина диаграммы направленности антенны должна быть меньше интервала однозначного измерения угловой координаты.
ВОПРОС №14 Способы определения высоты полета цели (расчетный и V-луча). 2.1. Определение высоты полета цели расчетным методом
Запишем выражение (2.2) (учитывая, что
Представим (2.2) как:
Используя приближенное разложение квадратного корня в степенной ряд
Упростив выражение, получим:
Учитывая, что радиус земного шара R = 6368 км, находим
Причем все величины должны быть выражены в км. В реальных РЛС расчет высоты производится по следующей зависимости:
где: 2.2. Определение высоты методом V – образного луча.
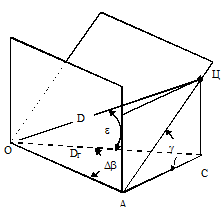
Определение высоты основано на следующем: антенная система вращается таким образом, что цель вначале попадает в зону действия вертикального луча, а затем наклонного. Угол Db рис (1.10) на который поворачивается антенная система от момента облучения цели вертикальным лучам до момента облучения наклонным лучом, зависит от угла места цели, что при известной дальности позволяет определить высоту цели. Таким образом определение высоты сводится к определению наклонной дальности до цели и угла Db. Формула, определяющая зависимость высоты от угла Db и дальности до цели может быть получена при помощи геометрических построений, приведенных на рис.. Заменяя движение лучей относительным движением объекта, обозначим точки пересечения объекта с плоскостями через Б и А. При этом ОБ = ОА = D, ОВ = ОД = DГ. (DГ – горизонтальная дальность до цели).
Из треугольника ОБД получим:
Решая совместно два последних соотношения, получим:
Определение малых высот, связанное с измерением малых углов Db не может быть точным. Для повышения точности измерения данным способом целей летящих на малой высоте ДНА верхних и нижних лучей раздвигаются на угол D (обычно его выбирают равным 100), т.е. вводится дополнительный угол запаздывания второй отметки относительно первой и при расчете высоты вместо измеренного угла Db необходимо подставить угол Db- D. среднеквадратическая ошибка определения высоты данным способом составляет 150 – 300 м в зависимости от пространственного положения цели относительно РЛС. Возможен другой вариант нахождения высоты цели методом V – луча по измеренным значениям наклонной дальности и угла Db. Из рис. 1.10 видно, что
Но т.к. ЦС=АСtgg, а g=450, то Н=ЦС=АС, тогда справедливо равенство:
Подставив (2) в (1) получим: Последнее равенство позволяет рассчитать значение угла места по измеренному углу Db. При этом в соответствии с равенствами (1,2) и (3) высота цели равна:
Поскольку РЛС измеряет наклонную дальность до цели, которая связана с горизонтальной соотношением:
Используя известное тригонометрическое выражение
Подставив (6) в (5), а последнее в (4) получим:
ВОПРОС №15
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1939; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.247 (0.007 с.) |

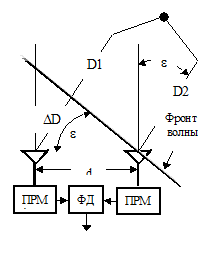 Фазовый метод пеленгации предусматривает использование антенн в точках 1 и 2, разнесенных в пространстве на расстояние d. Принимаемые ими колебания проходят от их источника расстояния D1 и D2, разность которых
Фазовый метод пеленгации предусматривает использование антенн в точках 1 и 2, разнесенных в пространстве на расстояние d. Принимаемые ими колебания проходят от их источника расстояния D1 и D2, разность которых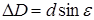
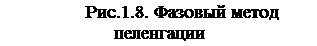
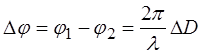

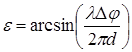

 , тогда:
, тогда: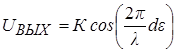
 не выходит за пределы p (от – 0.5p до 0.5p), что соответствует:
не выходит за пределы p (от – 0.5p до 0.5p), что соответствует: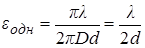
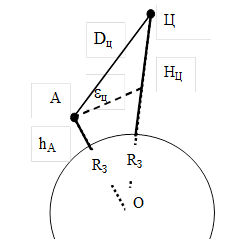 Измерение высоты цели может осуществляться на основе координатной информации (рис.3.1). Высоту цели относительно земной поверхности можно найти измеряя на РЛС наклонную дальность до цели DЦ и угол азимута e. Для точного измерения высоты цели необходимо учесть атмосферную рефракцию и кривизну Земли. Нормальная атмосферная рефракция, соответствующая стандартной атмосфере, может быть приближенно учтена переходом от действительного радиуса земного шара RЗ к эффективному RЭ=4/3 RЗ. В таком случае, пользуясь геометрией рисунка (3.1) из треугольника ОАЦ по теореме косинусов определим сторону ОЦ:
Измерение высоты цели может осуществляться на основе координатной информации (рис.3.1). Высоту цели относительно земной поверхности можно найти измеряя на РЛС наклонную дальность до цели DЦ и угол азимута e. Для точного измерения высоты цели необходимо учесть атмосферную рефракцию и кривизну Земли. Нормальная атмосферная рефракция, соответствующая стандартной атмосфере, может быть приближенно учтена переходом от действительного радиуса земного шара RЗ к эффективному RЭ=4/3 RЗ. В таком случае, пользуясь геометрией рисунка (3.1) из треугольника ОАЦ по теореме косинусов определим сторону ОЦ:
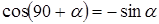 ) в виде:
) в виде:
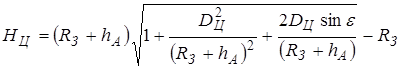
 , при
, при  получим:
получим: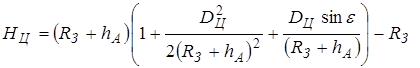
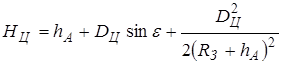
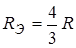 =8500. Подставляя это значение в и пренебрегая малостью величины
=8500. Подставляя это значение в и пренебрегая малостью величины 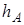 по сравнению с
по сравнению с 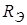 получим:
получим: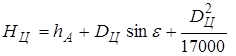
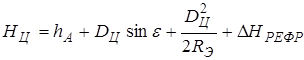
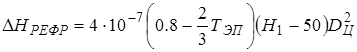 поправка на рефракцию, причем: Н1 значение высоты соответствующее углу места цели
поправка на рефракцию, причем: Н1 значение высоты соответствующее углу места цели 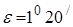 и стандартной рефракции,
и стандартной рефракции, 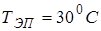 - значение эквивалентной приведенной температуры при стандартной рефракции. В ряде РЛС в ЦВС записаны
- значение эквивалентной приведенной температуры при стандартной рефракции. В ряде РЛС в ЦВС записаны  и e для расчета Н1 соответствующее нормальной рефракции.
и e для расчета Н1 соответствующее нормальной рефракции.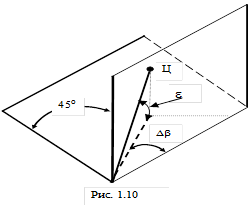 Станция с V – образным лучом дает возможность определить все три координаты цели. Определение дальности и азимута производится с помощью вертикального луча, а высота при помощи вертикального и наклонного.
Станция с V – образным лучом дает возможность определить все три координаты цели. Определение дальности и азимута производится с помощью вертикального луча, а высота при помощи вертикального и наклонного.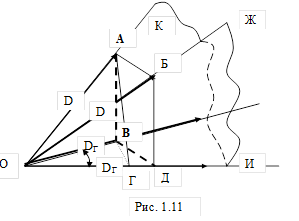 Проводим сечение АВГ, перпендикулярное линии ОИ (линии пересечения плоскостей ОЖИ и ОКИ); угол АГВ = 450, угол АВГ = 90 0 следовательно, треугольник ГВА равнобедренный и ВГ = АВ = НЦ. Из треугольника ОВГ имеем:
Проводим сечение АВГ, перпендикулярное линии ОИ (линии пересечения плоскостей ОЖИ и ОКИ); угол АГВ = 450, угол АВГ = 90 0 следовательно, треугольник ГВА равнобедренный и ВГ = АВ = НЦ. Из треугольника ОВГ имеем: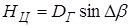

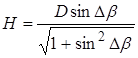
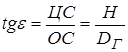 (1)
(1)
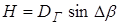 (2)
(2)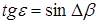 (3)
(3)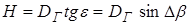 (4)
(4)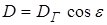 (5)
(5)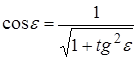 , которое для нашего случая примет вид:
, которое для нашего случая примет вид: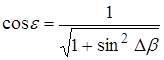 (6)
(6)



