
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для составления системы необходимо выбрать направления токов в ветвяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система уравнений решается и находятся неизвестные токи. Доп. уравнение: 1.6. Принцип и метод наложения в теории цепей. Принцип наложения или суперпозиции – это физический принцип, который говорит, что результирующее действие, возникающее от воздействия нескольких сил, может быть в линейной системе найдено как алгебраическая сумма от действий каждой силы в отдельности. В теории цепей под силой рассматривается воздействие каждого источника. Тогда можно заключить, что ток, который возникает на участке цепи под действием нескольких источников, работающих одновременно, можно определить как алгебраическую сумму частичных токов, каждый из которых возникает под действием своего источника, работающего отдельно от остальных источников. Это применимо только для линейных цепей (систем). К линейным относят цепи, свойства и параметры которых не зависят от величин, направлений токов и напряжений в элементах цепи. Частичные токи рассчитываются каждый в своей схеме замещения, в которой оставляют один источник, а остальные заменяют следующим образом: идеальный источник тока – разрывом (J=0), идеальный источник напряжения – перемычкой, проводником (E=0), реальные источники энергии – внутренними сопротивлениями. К полученным схемам применяют законы Кирхгофа, законы Ома. На основе этих положений возникает метод наложения для расчетов токов и напряжений. Особенно он необходим, когда в цепи действует несколько разнотипных источников (например, с разными частотами, с разными видами действия, с разной формой воздействия). Рассмотрим на примере. Пример 1
Составим четыре схемы замещения, в каждой из которых будет действовать только один источник энергии и протекать частичные токи от этого источника.
1) При этом надо учитывать направления частичных токов источников.
3)
4)
В итоге определяют токи от всех источников, например, I1=I1E1+I1J2+I1E3+I1E4 Как мы видим, в данном примере решение было бы легче при применении метода токов ветвей. 1.7. Метод контурных токов 1. Недостатки МТВ Основной недостаток – довольно большое количество уравнений и соответственно трудоемкость работы. Поэтому были разработаны другие методы, в частности метод контурных токов (МКТ) и метод узловых напряжений или потенциалов (МУН), где получается меньше уравнений. 2. Основы МКТ В качестве неизвестных здесь используются так называемые контурные токи. Это некоторые условные мысленные токи, протекающие по выбранным независимым контурам. В качестве дополнительных неизвестных берутся напряжения на идеальных источниках тока. Система уравнений составляется только на основе второго закона Кирхгофа с применением закона Ома. Конкретные токи ветвей (действительные токи) определяются как алгебраическая сумма соответствующих контурных токов, протекающих через ветвь. 3. Определение числа уравнений и выбор контуров для МКТ Количество уравнений определяется по формуле:
Контуры выбираются так, чтобы в них не входили идеальные источники тока (основные контуры). Дополнительные контуры выбираются с одним источником тока. Их уравнения в систему не включаются, но их влияние учитывается при решении системы. 4. Пример использования
NB=5, NУЗ=3, NHK=3, NИИТ(J)=1.
Решив данную систему и определив контурные токи, найдем токи ветвей следующим образом:
Для определения напряжения на источнике тока составляется вспомогательное уравнение по закону Кирхгофа для дополнительного (3) контура: Можно выделить алгоритм расчета: Определение количества уравнений Выбор основных и дополнительных контуров Составление системы уравнений для контурных токов Решение системы уравнений Определение токов ветвей
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.57 (0.008 с.) |

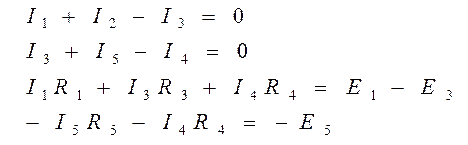
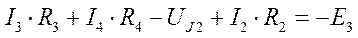 . Из него находят UJ2.
. Из него находят UJ2.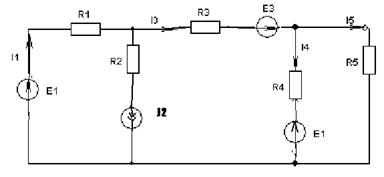 К данной схеме можно применить как метод наложения, так и метод токов ветвей.
К данной схеме можно применить как метод наложения, так и метод токов ветвей.
 2)
2)


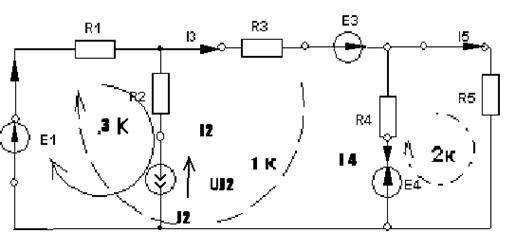
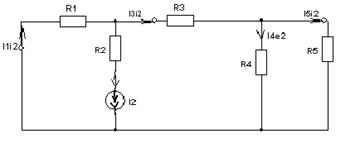
 Выбираем 1 и 2 контуры без идеальных источников тока. Составляем систему уравнений для основных контуров (1 и 2), используя контурные токи I1К,I2К, причем I3К=J2.
Выбираем 1 и 2 контуры без идеальных источников тока. Составляем систему уравнений для основных контуров (1 и 2), используя контурные токи I1К,I2К, причем I3К=J2.
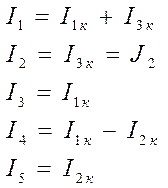

 . Отсюда определяется UJ2.
. Отсюда определяется UJ2.


