
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 11. Расчет переходных процессов при воздействии э.д.с. произвольной формы.Содержание книги
Поиск на нашем сайте
В операторном методе расчета отпадает необходимость определения постоянных интегрирования по начальным условиям, т.к. начальные условия учитываются при составлении алгебраических уравнений для изображений искомых величин. Этим и объясняется широкое применение этого метода. Преобразование Лапласа. Сущность операторного метода расчета переходных процессов состоит в том, что функцию Операторное изображение
Функция Переход от изображения
где Таким образом, в результате преобразований получается пара однозначных соответствий:
Для многих функций такие соответствия найдены и сведены в таблицы. При применении операторного метода система интегро-дифференциальных уравнений относительно оригиналов В результате решения полученной системы алгебраических уравнений находят изображения Рассмотрим наиболее важные свойства преобразования Лапласа, представляющих интерес для анализа электрических цепей. Применение преобразования Лапласа к решению линейных интегро-дифференциальных уравнений основано на свойстве линейности и преобразованиях операций дифференцирования и интегрирования во временной области. Свойство линейности записывается следующим образом:
т.е. при умножении оригинала на постоянную величину, изображение также умножается на эту величину, а изображение суммы равно сумме изображений. Операциям дифференцирования и интегрирования оригиналов (в t-области) соответствуют более простые операции умножения и деления их изображений (в p – области):
где Свойства преобразования Лапласа позволили в теории цепей ввести понятие операторных функций (сопротивления и проводимости) и операторных передаточных функций цепи. При этом оказалось возможным составлять схему замещения электрической цепи в операторной форме, а по ней сразу составлять уравнения для изображений, минуя составление интегро-дифференциальных уравнений для оригиналов. Операторные уравнения для элементов электрической цепи получают из соответствующих уравнений, связывающих мгновенные значения напряжений и токов. Закон Ома и Кирхгофа в операторной форме.
Запишем закон Ома для мгновенных значений после коммутации:
Перейдем от закона Ома, записанного для мгновенных значений к его выражению в операторной форме.
закон Ома в операторной форме.
Если
Законы Кирхгофа: Сумма изображений токов в узле электрической цепи равно нулю.
Для любого замкнутого контура, состоящего из
Закон Кирхгофа при нулевых начальных условиях: Эквивалентные операторные схемы замещения для элементов электрической цепи. Наиболее рациональный путь применения преобразования Лапласа для анализа цепи состоит в непосредственном составлении алгебраических уравнений для изображений по операторной или эквивалентной схеме замещения в частотной области. На этой схеме вместо напряжений и токов указаны их изображения, а элементы представляются операторными схемами замещения. Рассмотрим операторные схемы замещения элементов электрической цепи. 1. Резистивный элемент. Резистор с сопротивлением R характеризуется уравнением
Резистор характеризуется операторным сопротивлением R или проводимостью G.
2. Индуктивный элемент. Напряжение и ток в индуктивности связаны соотношением
где
Начальный ток в индуктивности учитывается в виде дополнительных источников: источника напряжения 3. Емкостной элемент. Напряжение и ток на емкости связаны соотношением где
Начальный заряд на конденсаторе учитывается в виде дополнительных источников: источника тока с током Источникам э.д.с. е(t) и тока j(t) соответствуют источники с операторным напряжением Общая методика анализа переходных процессов операторным методом. Операторный метод анализа переходных процессов можно свести к следующему: 1) составление операторной схемы замещения с учетом начальных условий и по ней составление алгебраических уравнений для изображений по тому или иному методу расчета; 2) решение их относительно изображений искомых реакций; 3) нахождение оригиналов искомых функций по их найденным изображениям. Расчет сложных электрических цепей операторным методом не всегда можно свести к известным табличным формулам. Использование же обратного преобразования Лапласа для отыскания оригинала по известному изображению может оказаться трудной задачей. В таких случаях используется теорема разложения. Теорема разложения позволяет находить оригиналы по известному изображению. В теории цепей очень часто операторное изображение искомой функции (тока или напряжения) имеет вид рациональной дроби:
где Полюса функции определяются корнями уравнения 1. Пусть все корни уравнения Тогда переход от изображения к функции времени производят с помощью формулы:
где
Таким образом,
Эта формула называется теоремой разложения. В частном случае, когда в составе знаменателя есть множитель
Выделенный постоянный член представляет собой принужденную составляющую тока или напряжения. Если
Если есть еще и нулевой корень, то
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 вещественной переменной
вещественной переменной  , называемую оригиналом, заменяют функцией
, называемую оригиналом, заменяют функцией  комплексной переменной
комплексной переменной  , называемой изображением. Комплексное число
, называемой изображением. Комплексное число  называется оператором.
называется оператором. и оригинал связаны с помощью прямого преобразования Лапласа:
и оригинал связаны с помощью прямого преобразования Лапласа: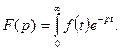
 должна удовлетворять условиям Дирихле. Практически все функции, встречающиеся в теории электрических цепей, удовлетворяют условиям Дирихле.
должна удовлетворять условиям Дирихле. Практически все функции, встречающиеся в теории электрических цепей, удовлетворяют условиям Дирихле.
 - вещественная часть оператора
- вещественная часть оператора 
 где а – постоянная,
где а – постоянная,

 - начальное значение функции, при
- начальное значение функции, при 



 -операторное сопротивление участка цепи,
-операторное сопротивление участка цепи, - представляет собой внутреннюю э.д.с., обусловленную запасом энергии в магнитном поле индуктивности, вследствие протекания тока непосредственно до коммутации,
- представляет собой внутреннюю э.д.с., обусловленную запасом энергии в магнитном поле индуктивности, вследствие протекания тока непосредственно до коммутации, - представляет собой внутреннюю э.д.с., обусловленную запасом энергии в электрическом поле конденсатора, вследствие наличие напряжения
- представляет собой внутреннюю э.д.с., обусловленную запасом энергии в электрическом поле конденсатора, вследствие наличие напряжения  , непосредственно до коммутации.
, непосредственно до коммутации. ,
,
 - проводимость в операторной форме.
- проводимость в операторной форме.
 ветвей имеем:
ветвей имеем:
 .
. переходя к изображению, получим операторное уравнение:
переходя к изображению, получим операторное уравнение: где
где  или
или 
 переходя к изображениям, получим операторные уравнения:
переходя к изображениям, получим операторные уравнения: , или
, или 
 - значение тока в момент времени
- значение тока в момент времени  Этим выражениям соответствуют операторные эквивалентные схемы индуктивности. Индуктивность характеризуется операторным сопротивлением
Этим выражениям соответствуют операторные эквивалентные схемы индуктивности. Индуктивность характеризуется операторным сопротивлением  (проводимостью
(проводимостью  ), а начальное значение тока
), а начальное значение тока  учитывается в виде последовательного источника э.д.с.
учитывается в виде последовательного источника э.д.с.  или параллельного источника тока
или параллельного источника тока 
 , соединенного последовательно с индуктивным элементом и имеющую полярность, совпадающую с направлением начального тока и источника тока
, соединенного последовательно с индуктивным элементом и имеющую полярность, совпадающую с направлением начального тока и источника тока  , соединенного параллельно индуктивной проводимости и направленного одинаково с начальным током.
, соединенного параллельно индуктивной проводимости и направленного одинаково с начальным током. Для изображений получаем:
Для изображений получаем: 
 - начальное значение напряжения, в момент t=0.
- начальное значение напряжения, в момент t=0. Операторные схемы замещения для емкости:
Операторные схемы замещения для емкости: , соединенного параллельного емкостной проводимости и направленного в сторону обкладки, имеющей положительный заряд и источника напряжения с напряжением
, соединенного параллельного емкостной проводимости и направленного в сторону обкладки, имеющей положительный заряд и источника напряжения с напряжением  , соединенного последовательно с емкостным сопротивлением и имеющую полярность, совпадающую с полярностью начального заряда.
, соединенного последовательно с емкостным сопротивлением и имеющую полярность, совпадающую с полярностью начального заряда. и током
и током  .
. ,
, и
и  - многочлены различных степеней p. Причем и числитель и знаменатель не имеют общих корней.
- многочлены различных степеней p. Причем и числитель и знаменатель не имеют общих корней. Нули функции определяются корнями уравнения
Нули функции определяются корнями уравнения 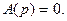
 простые.
простые.
 - корни уравнения
- корни уравнения 
 - производная многочлена
- производная многочлена  .
. .
. , а в составе
, а в составе  уже нет нулевого корня и уравнение
уже нет нулевого корня и уравнение  имеет
имеет 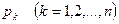 , то формула разложения примет следующий вид:
, то формула разложения примет следующий вид:
 , то
, то




