
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
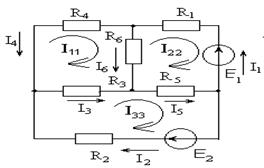
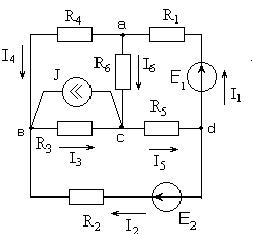
Данная схема имеет четыре узла и шесть ветвей.Содержание книги
Поиск на нашем сайте
Система уравнений по законам Кирхгофа имеет следующий вид:
Имеем систему из шести уравнений с шестью неизвестными. Выразив токи I1, I2, I5 через I4, I6,I3, получим:
Решая данную систему уравнений, можно найти токи ветвей. Число совместно решаемых уравнений равно числу ветвей схемы (числу неизвестных токов ветвей), поэтому в общем случае применение законов Кирхгофа для расчета сложных цепей не всегда
целесообразно. Количество совместно решаемых уравнений сокращается при использовании метода контурных токов и узловых потенциалов. В качестве переменных в методе контурных токов принимаются контурные токи. В схеме выделяют независимые контуры. В каждом контуре произвольно выбирают направление контурных токов. За контурные токи удобно принять токи внешних ветвей схемы, которые входят только в данный контур. Уравнения составляются на основе второго закона Кирхгофа, выражая токи ветвей через контурные токи. Для каждого контура пишем второй закон Кирхгофа:
Выразим токи ветвей через контурные:
После преобразования получим следующую систему уравнений:
Решив систему уравнений относительно контурных токов, находятся токи ветвей. Правильность решения по методу контурных токов осуществляется на основании второго закона Кирхгофа. Баланс мощностей.Пусть в электрической цепи произвольной конфигурации имеются источники и приемники электрической энергии. Сумма мощностей
Мощность, потребляемая всеми элементами цепи равна нулю. Математическая форма записи баланса мощностей:
Суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи. Метод узловых потенциалов является наиболее общим и широко применяется для анализа цепей любой конфигурации. При расчете электрических цепей методом узловых потенциалов потенциал одного из узлов принимается равным нулю. Для всех остальных узлов составляют уравнения по первому закону Кирхгофа. Решив систему уравнений, определяют потенциалы узлов. Затем по закону Ома определяют токи ветвей. Для приведенной схемы электрической цепи, составим уравнения по методу узловых потенциалов.
Выразим токи по закону Ома через потенциалы узлов: Подставим эти выражение в уравнения по первому закону Кирхгофа и приведя подобные члены получим следующее уравнение:
где: Решение системы уравнений позволяет определить потенциалы узлов, а по известным потенциалам токи ветвей. Проверку правильности решения осуществляется на основании первого закона Кирхгофа.
Основные свойства электрических цепей. Теорема Телледжена:Сумма произведений напряжений и токов всех ветвей схемы, удовлетворяющих законам Кирхгофа равна нулю: Свойство (принцип) взаимности.Пусть в схеме произвольной конфигурации в ветви Теорема компенсации. Любое сопротивление схемы Кроме того, любую ветвь с током можно заменить источником тока, направление которого совпадает с направлением тока ветви, без изменений токов и напряжений всех ветвей схемы. Принцип наложения. Метод наложения. Согласно принципу наложения, ток (напряжение) в любой ветви электрической цепи при одновременном действии нескольких источников представляет собой алгебраическую сумму частичных токов (напряжений), обусловленных каждым источником в отдельности. Частичными токами, напряжениями называются такие токи и напряжения, которые вызваны действием только одного источника. Применение принципа наложения дает метод наложения для расчета электрических цепей. Токи ветвей в исходной схеме, определяются как алгебраическая сумма частичных токов.
Теорема об эквивалентном источнике напряжения.Теорема об эквивалентном источникенапряжения (теорема Тевенина) формулируется следующим образом: ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником (генератором) напряжения с напряжением, равным напряжению холостого хода на зажимах разомкнутой ветви и внутренним сопротивлением, равным эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви. Используя теорему об эквивалентном источнике, можно определить ток в любой ветви электрической цепи, например Ток Напряжение
Теорема об эквивалентном источнике тока (теорема Нортона): ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник к которому подключена данная ветвь, заменить эквивалентным источником тока с током, равным току короткого замыкания этой ветви, и внутренней проводимостью, равной эквивалентной входной проводимости со стороны разомкнутой ветви.
Основная литература: 1[31-37, 43 -44, 49 – 56]; 1[27 – 31, 36 – 43, 45 - 49]; 2[24 – 29, 46 -49, 52, 56-59]; 2[15 – 21, 29 -35, 39- 46]. Дополнительная литература: 9[11-22]; 9 [32-41, 67-71, 90, 96-102]; 9 [56-66]. Контрольные вопросы: 1. Определить эквивалентное сопротивление двух резисторов с равными сопротивлениями, соединенных параллельно. 2. Определить эквивалентное сопротивление трех резисторов с равными сопротивлениями, соединенных параллельно. 3. Число линейно-независимых уравнений по первому закону Кирхгофа? 4. Число линейно-независимых уравнений по второму закону Кирхгофа? 5. Число линейно-независимых уравнений составленных по законам Кирхгофа для нахождения токов в ветвях электрической цепи. 6. Число линейно-независимых уравнений по методу контурных токов. 7. Мощность источника напряжения, мощность источника тока. 8. В цепи несколько источников напряжения. По какому признаку определяется режим работы источников питания.
9. Число линейно-независимых уравнений составленных по методу узловых потенциалов? 10. Особенности составления узловых уравнений при наличии ветви с идеальным источником напряжения. 11. Как определить токи ветвей, если известны потенциалы узлов? 12. В каких случаях применяется метод эквивалентного источника? 13. Как определить параметры эквивалентного источника напряжения? 14. Как найти параметры эквивалентного источника тока? 15. Какой двухполюсник называется пассивным? 16. Какой двухполюсник называется активным?
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.13.192 (0.01 с.) |



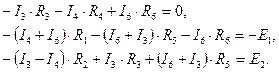



 всех ветвей такой электрической цепи равно нулю:
всех ветвей такой электрической цепи равно нулю:
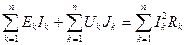 .
. Примем потенциал узла d равным нулю, т.е.
Примем потенциал узла d равным нулю, т.е. 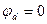 запишем первый закон Кирхгофа для узлов а,в,с.
запишем первый закон Кирхгофа для узлов а,в,с.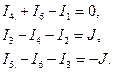
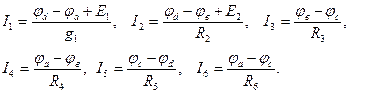

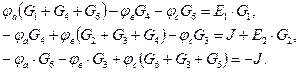
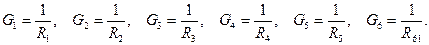
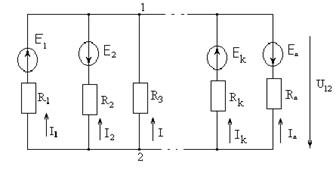 Метод двух узлов. Очень часто встречаются схемы с двумя узлами и с произвольным числом ветвей. Для нахождения токов ветвей необходимо определить напряжение между двумя узлами. Напряжение между двумя узлами:
Метод двух узлов. Очень часто встречаются схемы с двумя узлами и с произвольным числом ветвей. Для нахождения токов ветвей необходимо определить напряжение между двумя узлами. Напряжение между двумя узлами: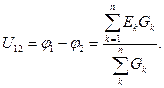
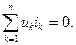 Данное выражение выражает закон сохранения энергии, каждое слагаемое представляет мощность потребляемую k- ветвью.
Данное выражение выражает закон сохранения энергии, каждое слагаемое представляет мощность потребляемую k- ветвью. действует единственный источник э.д.с.
действует единственный источник э.д.с.  , который создают ток
, который создают ток 
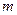 . Соответственно, э.д.с.
. Соответственно, э.д.с. 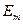 в ветви
в ветви  ток
ток 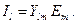 Электрические цепи, для которых выполняется условие
Электрические цепи, для которых выполняется условие 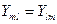 называются обратимыми цепями. Отношение
называются обратимыми цепями. Отношение  Если принять
Если принять 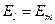 , то
, то  . Для обратимых цепей справедливо следующее, если некоторая э.д.с., действующая в какой-либо ветви электрической цепи (
. Для обратимых цепей справедливо следующее, если некоторая э.д.с., действующая в какой-либо ветви электрической цепи (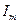 в первом случае, т.е.
в первом случае, т.е. 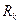 с током
с током 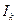 можно заменить источником э.д.с.
можно заменить источником э.д.с.  , направление которой противоположно направлению тока. При этом токи и напряжения всех ветвей схемы не изменяются. В общем случае любую ветвь с напряжением можно заменить источником э.д.с.:
, направление которой противоположно направлению тока. При этом токи и напряжения всех ветвей схемы не изменяются. В общем случае любую ветвь с напряжением можно заменить источником э.д.с.:  .
.

 .
. .
.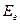 определяется из режима разомкнутой ветви и равно:
определяется из режима разомкнутой ветви и равно: 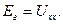
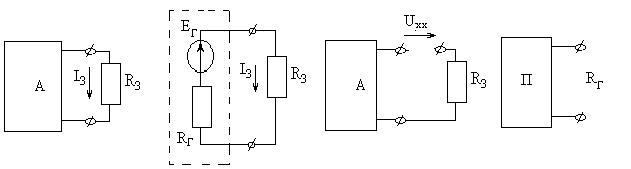

 , где
, где  - ток короткого замыкания ветви.
- ток короткого замыкания ветви.


