
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 7. Резонансные явления в линейных электрических цепях. Частотные характеристики пассивных двухполюсников. Практическое значение резонанса в электрических цепях. Явление взаимной индукцииСодержание книги
Поиск на нашем сайте
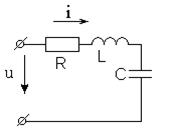
Рассмотрим изменение тока и напряжений на элементах цепи при синусоидальном входном воздействии
Согласно, второго закона Кирхгофа Запишем это уравнение в комплексной форме:
Мгновенное значение тока: Напряжение на элементах:
Токи и напряжения на различных участках электрической цепи синусоидального тока по фазе не совпадают. Наглядное представление о фазовом расположении различных векторов дает векторная диаграмма. На векторной диаграмме закон Кирхгофа выполняется в векторной форме:
Различают три режима в цепи, в зависимости от параметров цепи индуктивный, емкостный, активный. Рассмотрим параллельное соединение R, L,C элементов при синусоидальном воздействии
Согласно, первому закону Кирхгофа ток в неразветвленной части цепи
Напряжение на всех элементах Перейдем к уравнению в комплексной форме:
где:
Токи в элементах:
мгновенные значения токов:
В цепи в зависимости от параметров различают индуктивный характер, емкостный характер, активный характер. Рассмотрим произвольный двухполюсник при действии источника синусоидального напряжения:
Мгновенная мощность:
мгновенная мощность, поступающая в цепь, состоит из двух слагаемых – постоянной составляющей и синусоидальной составляющей, имеющую удвоенную частоту по сравнению с частотой напряжения и тока. Среднее значение мощности за период называется активной мощностью:
Амплитуда синусной составляющей мгновенной мощности численно равна полной мощности:
Реактивная мощность
В электрической цепи содержащей источники гармонических э.д.с. и токов для мгновенных мощностей выполняется соотношение, т.е. справедлива теорема Теледжена: сумма мгновенных мощностей всех ветвей электрической цепи равна нулю: В комплексной форме можно записать
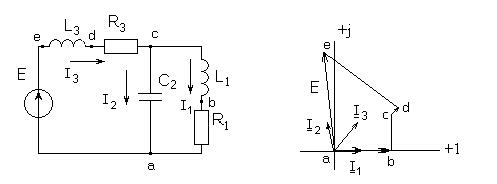
т.е. активная мощность, рассеиваемая в сопротивлениях равна активной мощности источников энергии, реактивная мощность в реактивных элементах равна реактивной мощности источников энергии. Реактивная мощность индуктивностей учитывается со знаком плюс, а емкостей со знаком минус. Активная потребляемая мощность измеряется ваттметром. Методы анализа электрических цепей синусоидального тока. Все методы расчета цепей постоянного тока получены на основе законов Кирхгофа. Если повторить все рассуждения и выводы, взяв за основу уравнения Кирхгофа в комплексной форме, то для цепей синусоидального тока можно обосновать все методы, которые получены для цепей постоянного тока. С учетом этого, все методы расчета электрических цепей постоянного тока (метод эквивалентного преобразования электрических цепей, метод контурных токов, метод узловых потенциалов, метод наложения, метод активного двухполюсника), эквивалентные преобразования электрических цепей справедливы и для цепей синусоидального тока. Соответствующие соотношения записываются в комплексной форме, т.е. рассматривается символический метод расчета. Несмотря на общность методов расчета цепей синусоидального и постоянного токов, расчеты цепей синусоидального тока значительно сложнее. Например, написать уравнения по методу контурных токов для приведенной схемы электрической цепи.
Топографическая диаграмма. Совокупность точек на комплексной плоскости, изображающих собой комплексные потенциалы одноименных точек электрической схемы, называется топографической диаграммой. При построении топографической диаграммы потенциал одной из точек схемы принять равным нулю. На диаграмме эта точка помещается в начало координат. Тогда положение остальных точек схемы на диаграмме будет вполне определенным. Рассмотрим построение потенциальной диаграммы. Построить потенциальную диаграмму для цепи, изображенной на рисунке, если Примем потенциал точки а равным нулю
Потенциалы точек a,b,c,d,e отложены на комплексной плоскости. Топографическая диаграмма показана на рисунке. Последовательное соединение элементов
При резонансе напряжения, входное сопротивление становится чисто резистивным, реактивное входное сопротивление равно нулю Резонансная частота контура определяется из соотношения Напряжения на реактивных элементах равны по величине и противоположны по направлению. Реактивные мощности тоже равны
Отношение напряжений на реактивных элементах к приложенному напряжению, или отношение реактивных мощностей к активной мощности в режиме резонанса называется добротностью контура
Добротность контура указывает во сколько раз напряжение на индуктивности и емкости при резонансе больше, чем напряжение приложенное к цепи. Векторная диаграмма в момент резонанса. Параллельное соединение элементов Напряжение на зажимах цепи Ток в неразветвленной части:
При резонансе токов При резонансе Добротность параллельного контура, показывает во сколько раз ток в реактивных элементах при резонансе больше тока на входе контура.
Частотные характеристики параллельного колебательного контура.
Частотные характеристики резонансных контуров. Зависимость параметров цепи от частоты называются частотными характеристиками. Зависимость действующих или амплитудных значений тока
Зависимость тока, напряжения на катушке, напряжения на конденсаторе от частоты:
Для удобства сравнения резонансных кривых друг с другом будем рассматривать зависимости:
Чем больше
Электрические цепи с взаимной индукцией. Явление наведения Э.Д.С. в каком-либо контуре при изменении тока в другом называется явлением взаимоиндукции. Наведенная э.д.с. называется э.д.с. взаимной индукции. Когда изменение тока в одном из элементов цепи приводит к появлению э.д.с. в другом элементе цепи, говорят, что эти два элемента индуктивно связаны. Магнитную связь обеих ветвей характеризуют коэффициентом взаимной индуктивности Физическим прообразом может служить устройство из двух близко расположенных катушек или катушек на общем сердечнике. В общем случае любое число катушек имеет индуктивную связь. Степень индуктивной связи характеризуется коэффициентом связи К, При протекании тока
На разомкнутых выводах второй катушки появляется напряжение взаимной индукции: Под действием тока Тогда напряжение на выводах катушек будет:
Приведенные уравнения можно записать в комплексной форме:
Если катушки включаются таким образом, что потоки самоиндукции Одноименными зажимами принято называть узлы относительно которых одинаково ориентированные токи создают складывающие потоки самоиндукции и взаимной индукции.
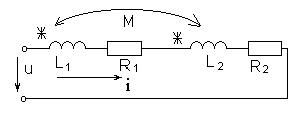
Согласное включение Встречное включение
Чтобы определить, как ориентированы между собой катушки, необходимо определить как ориентированы токи относительно одноименных зажимов. При одинаковой ориентации относительно одноименных зажимов – согласное включение, при разной ориентации – встречное включение. Определение взаимоиндукции опытным путем. Первый способ: Проделаем два опыта. Включаем катушки последовательно и согласно. Измерим ток и напряжение на входе и активную мощность цепи. Включим катушки последовательно и встречно. Измерим ток, напряжение. По результатам измерений определим:
Второй способ. Включим первую катушку к источнику синусоидальной э.д.с. через амперметр и измерим Согласное включение катушек: ток в элементах направлен одинаково относительно одноименных зажимов.
В комплексной форме:
где
Встречное включение катушек. Ток в элементах направлен противоположно относительно одноименных зажимов.
В комплексной форме:
Ток в цепи: Можно объединить обе формулы в одну:
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.169.56 (0.008 с.) |

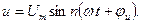

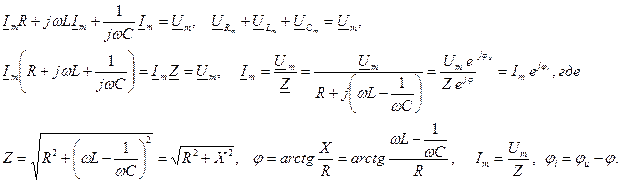
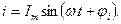
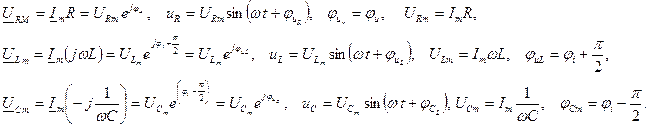
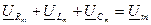


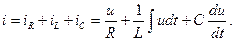
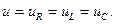
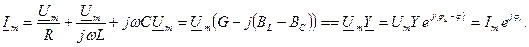
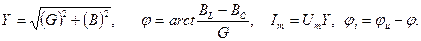
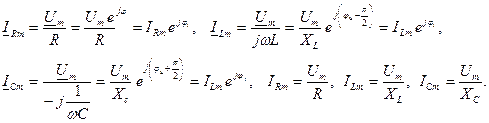
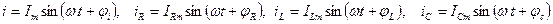 .
.

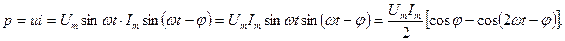
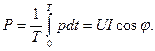
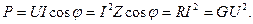
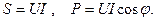
 называется коэффициентом мощности и является важной характеристикой электрических машин и линий передач. Чем выше
называется коэффициентом мощности и является важной характеристикой электрических машин и линий передач. Чем выше 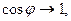 тем меньше потерь в линии и выше степень использования электрических машин и аппаратов. Максимальное значение
тем меньше потерь в линии и выше степень использования электрических машин и аппаратов. Максимальное значение  т.е. цепь носит чисто активный характер и сдвиг фаз между током и напряжением равен нулю.
т.е. цепь носит чисто активный характер и сдвиг фаз между током и напряжением равен нулю. Полную мощность рассматривают как модуль комплексной мощности:
Полную мощность рассматривают как модуль комплексной мощности: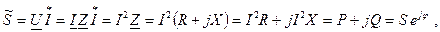
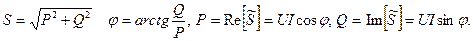
 - ток сопряженный току
- ток сопряженный току  , отличается противоположным знаком перед мнимой частью и перед аргументом.
, отличается противоположным знаком перед мнимой частью и перед аргументом.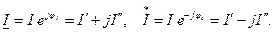

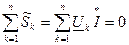 - сумма комплексных мощностей потребляемых всеми ветвями электрической цепи равна нулю.
- сумма комплексных мощностей потребляемых всеми ветвями электрической цепи равна нулю.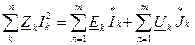 - баланс мощностей в комплексной форме.
- баланс мощностей в комплексной форме. - сумма комплексных мощностей, генерируемых источником э.д.с. и тока.
- сумма комплексных мощностей, генерируемых источником э.д.с. и тока.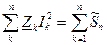 - сумма комплексных мощностей, потребляемая потребителями.
- сумма комплексных мощностей, потребляемая потребителями.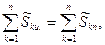 для выполнения этого условия необходимо выполнения двух условий:
для выполнения этого условия необходимо выполнения двух условий: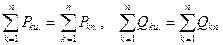 ,
, Составим уравнения по методу контурных токов, направив их по часовой стрелке:
Составим уравнения по методу контурных токов, направив их по часовой стрелке: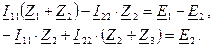
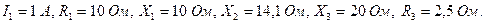
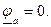
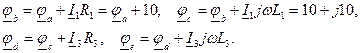
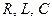 называется последовательным колебательным контуром, в нем возможен резонанс напряжения. Резонансомнапряжения называется такой режим в колебательном контуре, при котором частота источника э.д.с.
называется последовательным колебательным контуром, в нем возможен резонанс напряжения. Резонансомнапряжения называется такой режим в колебательном контуре, при котором частота источника э.д.с. 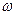 равна частоте собственных колебаний контура
равна частоте собственных колебаний контура  .
.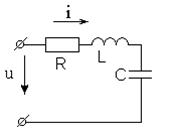 Входное напряжение
Входное напряжение 
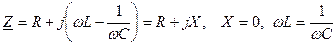 ,
, 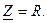
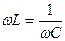 , т.е.
, т.е. 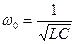 . Так как
. Так как 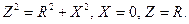 Полное сопротивление минимально, тогда ток в цепи
Полное сопротивление минимально, тогда ток в цепи  и активная мощность в режиме резонанса максимальны
и активная мощность в режиме резонанса максимальны 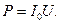
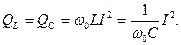
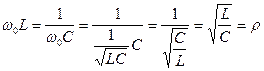 - характеристическое или волновое сопротивление контура.
- характеристическое или волновое сопротивление контура. - добротность контура.
- добротность контура.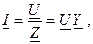 где
где 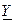 - входная комплексная проводимость.
- входная комплексная проводимость. , где
, где  - входная реактивная проводимость.
- входная реактивная проводимость. - резонансная частота контура.
- резонансная частота контура. ток через индуктивный элемент равен по модулю току через емкостной элемент и находится в противофазе и могут превышать входной ток.
ток через индуктивный элемент равен по модулю току через емкостной элемент и находится в противофазе и могут превышать входной ток. - добротность параллельного контура, показывает во сколько раз ток в реактивных элементах при резонансе больше тока на входе контура.
- добротность параллельного контура, показывает во сколько раз ток в реактивных элементах при резонансе больше тока на входе контура.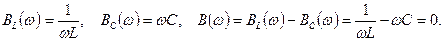
 и напряжений
и напряжений 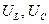 от частоты называется резонансными кривыми.
от частоты называется резонансными кривыми. - частотные характеристики цепи.
- частотные характеристики цепи.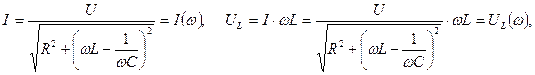

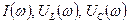 - резонансные кривые.
- резонансные кривые.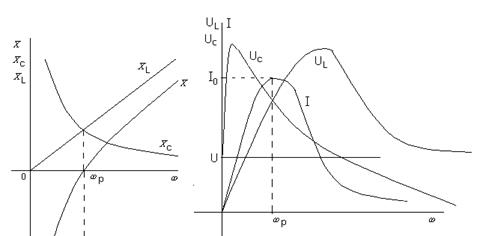

 , где
, где 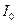 ток при резонансе,
ток при резонансе, 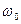 - резонансная частота.
- резонансная частота.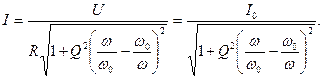
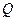 , тем острее резонансная кривая, тем лучше избирательные свойства цепи.
, тем острее резонансная кривая, тем лучше избирательные свойства цепи.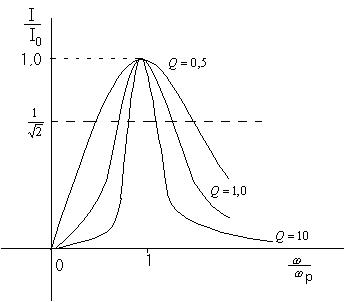
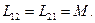
 где
где  и
и  индуктивность элементов цепи,
индуктивность элементов цепи,  - взаимная индуктивность.
- взаимная индуктивность. под действием напряжения
под действием напряжения  в катушке с индуктивностью
в катушке с индуктивностью 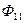 , сцепленный с витками первой катушки, и магнитный поток взаимной индукции
, сцепленный с витками первой катушки, и магнитный поток взаимной индукции 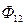 , сцепленный с витками второй катушки с индуктивностью
, сцепленный с витками второй катушки с индуктивностью  , где
, где  - коэффициент взаимной индукции катушек
- коэффициент взаимной индукции катушек  .
. . Пусть ток
. Пусть ток  протекает по второй катушке под действием напряжения
протекает по второй катушке под действием напряжения 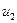 .
. На разомкнутых выводах первой катушки появляется напряжение взаимной индукции:
На разомкнутых выводах первой катушки появляется напряжение взаимной индукции: 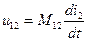 . По первой катушке течет ток
. По первой катушке течет ток 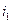 , а по второй течет ток
, а по второй течет ток 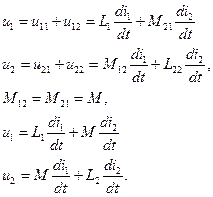
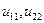 - напряжение самоиндукции первой и второй катушек,
- напряжение самоиндукции первой и второй катушек,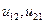 - напряжение взаимной индукции,
- напряжение взаимной индукции,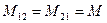 - взаимная индуктивность, величина алгебраическая, если
- взаимная индуктивность, величина алгебраическая, если  , напряжения взаимной индукции складываются с напряжением самоиндукции, если
, напряжения взаимной индукции складываются с напряжением самоиндукции, если 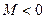 , напряжение взаимной индукции и самоиндукции вычитаются.
, напряжение взаимной индукции и самоиндукции вычитаются.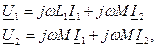
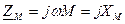 - комплексное сопротивление взаимной индукции,
- комплексное сопротивление взаимной индукции, - сопротивление взаимной индукции.
- сопротивление взаимной индукции.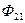 складываются, то такое включение катушек называется согласным. Если же потоки самоиндукции и взаимной индукции вычитаются, то такое включение катушек называется встречным. Для удобства изображения электрические цепи с взаимной индуктивностью вводят понятия одноименных зажимов.
складываются, то такое включение катушек называется согласным. Если же потоки самоиндукции и взаимной индукции вычитаются, то такое включение катушек называется встречным. Для удобства изображения электрические цепи с взаимной индуктивностью вводят понятия одноименных зажимов.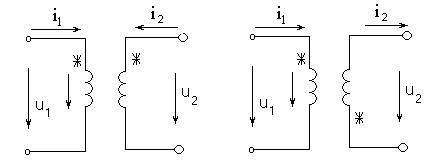
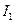 , а к зажимам второй подключим вольтметр с большим внутренним сопротивлением и измерим напряжение
, а к зажимам второй подключим вольтметр с большим внутренним сопротивлением и измерим напряжение 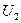 . Взаимоиндукция:
. Взаимоиндукция: 
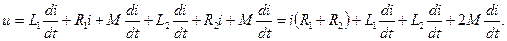
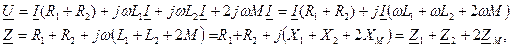
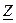 - входное комплексное сопротивление всей цепи при согласном включении двух катушек,
- входное комплексное сопротивление всей цепи при согласном включении двух катушек,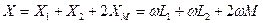 - реактивное сопротивление при согласном включении двух катушек. Ток в цепи:
- реактивное сопротивление при согласном включении двух катушек. Ток в цепи:
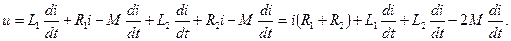


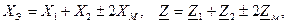
 где знак плюс соответствует согласному включению катушек, а минус соответствует встречному включению катушек.
где знак плюс соответствует согласному включению катушек, а минус соответствует встречному включению катушек.


