
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 14. Передаточные функции четырехполюсников.Содержание книги
Поиск на нашем сайте
При передаче сигналов связи на расстояние может участвовать большое число каскадно- включенных четырехполюсников.
Потери мощности сигнала при этом должны быть минимальными, а мощность сигнала выделяемая в нагрузке на приемном конце должна быть максимально возможной. Генератор с внутренним сопротивлением Zг отдает максимальную полную мощность в нагрузку, согласованную с его внутренним сопротивлением
Такой режим четырехполюсника, когда Характеристические параметры: характеристическое сопротивление — ZC, характеристическая постоянная передача —
Если четырехполюсник не симметричный:
Волновое или характеристическое сопротивление через параметры
Если симметричный А=D: Вторая характеристика позволяет сравнить напряжения и токи на входе и выходе четырехполюсника при согласованной нагрузке:
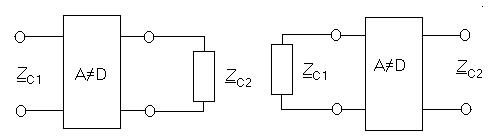
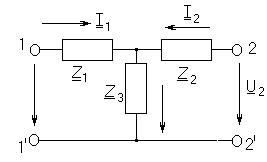
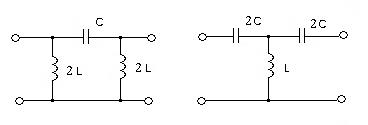
Очень удобно отношение напряжений на входе и выходе оценивать постоянной ослабления Эквивалентные схемы замещения пассивного четырехполюсника На основании уравнений четырехполюсника могут быть построены различные эквивалентные схемы замещения. На практике чаще всего пользуются Т- образной и П-образной схемами замещения четырехполюсников. 1. Т – образная схема замещения.
Формулы позволяют найти сопротивления
2. П — образные схемы четырехполюсников.
3. Г — образный фильтр
Зная коэффициенты A, B, C, D можно найти сопротивления:
Линейные пассивные четырехполюсники являются обратными, т.е. для них выполняется принцип взаимности. Отношение напряжения на входе к току на выходе (передаточное сопротивление входного и выходного контуров) не зависит от того, какие выводы являются входными, а какие – выходными Электрические фильтры. Низкочастотные фильтры. Высокочастотные фильтры. Фильтры типа m и k. Электрические фильтры – это четырехполюсники, которые без искажения пропускают сигналы частоты которых лежат в заданном диапазоне частот (в полосе пропускания) и с большим затуханием сигналы, частоты которых лежат в области задержки. Фильтр идеальный, если в полосе пропускания отсутствует ослабление сигнала и фаза частотная характеристика линейная, а вне полосы пропускания сигналы на выходе отсутствуют. Идеальный фильтр создать нельзя, но можно получить в полосе пропускания достаточно малое ослабление сигнала, если фильтр создан из конденсатора и катушек с малыми потерями. По полосе пропускания различают фильтры низкочастотные, высокочастотные, полосовые и заграждающие. Полоса пропускания низкочастотного фильтра от 0 до граничной частоты Коэффициент передачи по напряжению идеального фильтра в полосе пропускания равен 1. Фазочастотная характеристика в полосе пропускания линейная функция. Коэффициент затухания в полосе пропускания равен нулю. Схема низкочастотного фильтра:
Схема высокочастотного фильтра:
Частота среза фильтра НЧ: Фильтр НЧ пропускает без затухания частоты от нуля до частоты среза. Фильтр ВЧ пропускает от без затухания от частоты среза до бесконечности. Лекция № 15. Цепи с распределенными параметрами. Характеристики однородной линии. Длина волны и скорость распространения. Режимы работы линии. Условия для неискажающей линии. Линия без потерь. Частотные зависимости. Стоячие волны.
До сих пор мы рассматривали электрические цепи с сосредоточенными параметрами, предполагалось, что параметры электрической цепи Однако, рассматривая электромагнитные процессы, происходящие в электрических линиях, где происходит передача электроэнергии на расстояние, необходимо иметь в виду, что магнитное и электрическое поле распределены по всей длине линии и превращение электромагнитной энергии в тепло также происходит по всей длине линии. Здесь мы имеем дело с цепями с распределенными параметрами. В качестве цепи с распределенными параметрами рассматривается однородная двухпроводная линия. Однородная двухпроводная линия – это такая линия, индуктивность, емкость, активное сопротивление и проводимость которой равномерно распределены вдоль всей длины линии. Эти электрические параметры, отнесенные к единице длины линии, называются первичными параметрами линии; они обозначаются Уравнения однородной линии. Напряжение и ток в линии являются функциями двух независимых переменных – времени
Уравнение для приращений напряжений и тока на элементе длины
Разделив обе части на Эти уравнения известны под названием телеграфных уравнений. Если за начало отсчета принять конец линии
Уравнения могут быть решены однозначно при использовании начальных и граничных условий. Установившийся режим в однородной линии
Пусть ток и напряжения изменяются по синусоидальному закону с угловой частотой
Исключая ток, получим:
аналогично, исключая напряжение получим:
Введем следующее обозначение:
С учетом
Имеем дифференциальные уравнения второго порядка. Решение их имеет вид:
Тогда ток:
Для однородной линии, рассматриваемой между ее входными и выходными выводами как четырехполюсник, волновое сопротивление совпадает с характеристическим
Волновое сопротивление и коэффициент распространения называются вторичными параметрами однородной линии. Если выразить комплексные коэффициенты
Ток:
Каждое из слагаемых можно рассматривать как бегущую волну, движущуюся в направлении возрастания или убывания координаты и по мере увеличения расстояния
Характеристики однородной линии. Коэффициент распространения, коэффициент затухания, коэффициент фазы. Входное сопротивление линии. Коэффициент отражение волны. Согласованная нагрузка линии. Линия без потерь. Основная литература: 1[368 - 375], 2 [308 - 317]. Дополнительная литература: 9 [454 - 479]. Основная литература: 1 [212 – 223, 275 - 291], 2 [404 -408, 344 - 354]. Дополнительная литература: 9 [575 – 583, 513 - 535]. 1. Что характеризует статическое сопротивление? 2. Схема замещения нелинейного элемента на линейном участке ВАХ. 3. Уравнение однородной линии. 4. Первичные и вторичные параметры линии. 5. Линия без потерь.
Лабораторная работа № 1
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 999; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |


 Если между генераторам и нагрузкой находится четырехполюсник, то для передачи максимальной полной мощности от генератора в четырехполюсник необходимо согласовать входное сопротивление четырехполюсника Zвх1 с внутренним сопротивлением генератора, т.е. выполнить:
Если между генераторам и нагрузкой находится четырехполюсник, то для передачи максимальной полной мощности от генератора в четырехполюсник необходимо согласовать входное сопротивление четырехполюсника Zвх1 с внутренним сопротивлением генератора, т.е. выполнить:  , а дл я передачи максимально полной мощности от четырехполюсника в нагрузку — согласовать входное сопротивление четырехполюсника Zвх2 с сопротивлением генератора, т.е. выполнить условие:
, а дл я передачи максимально полной мощности от четырехполюсника в нагрузку — согласовать входное сопротивление четырехполюсника Zвх2 с сопротивлением генератора, т.е. выполнить условие: 
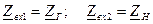 называется режимом согласованного включения.
называется режимом согласованного включения.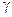 . Характеристическое сопротивление представляет собой такое комплексное сопротивление, при включении которого в качестве нагрузки входное сопротивление четырехполюсника становится равным:
. Характеристическое сопротивление представляет собой такое комплексное сопротивление, при включении которого в качестве нагрузки входное сопротивление четырехполюсника становится равным: 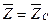 .
.
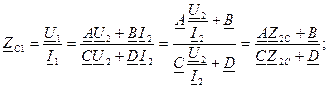
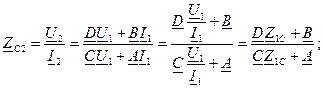



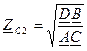
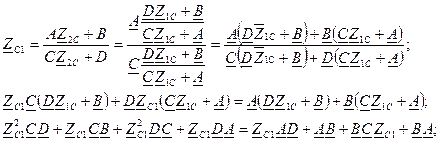
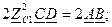
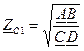

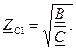
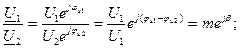
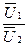 — характеризует изменения значения напряжения.
— характеризует изменения значения напряжения. — показывает сдвиг фаз между напряжениями на входе и выходе. Этот угол называется собственной или характеристической постоянной фазы.
— показывает сдвиг фаз между напряжениями на входе и выходе. Этот угол называется собственной или характеристической постоянной фазы.

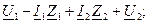



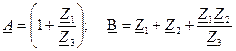

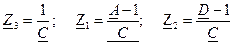
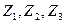 при коэффициентах четырехполюсника A, B, C, D.
при коэффициентах четырехполюсника A, B, C, D.


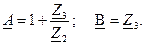


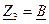




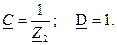
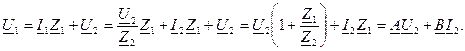

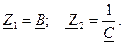

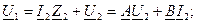


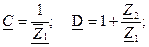


 Четырехполюсник называется симметричным если его характеристики не меняются при перемене местами входных и выходных выводов:
Четырехполюсник называется симметричным если его характеристики не меняются при перемене местами входных и выходных выводов:  .
. . Высокочастотного от
. Высокочастотного от  . Частотная характеристика фильтра коэффициент затухание:
. Частотная характеристика фильтра коэффициент затухание:  .
.

 Частота среза фильтра ВЧ:
Частота среза фильтра ВЧ: 
 сосредоточенны в различных ее точках.
сосредоточенны в различных ее точках. Однородная двухпроводная линия является очень распространенным типом линии.
Однородная двухпроводная линия является очень распространенным типом линии. и координаты
и координаты  . Однородную линию можно рассматривать в виде соединенных множества бесконечно малых элементов длиной
. Однородную линию можно рассматривать в виде соединенных множества бесконечно малых элементов длиной  . Каждый из которых имеет сопротивление
. Каждый из которых имеет сопротивление  индуктивность
индуктивность  , проводимость
, проводимость  , емкость
, емкость 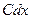 , где
, где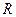 - сопротивление прямого и обратного провода
- сопротивление прямого и обратного провода - индуктивности петли, образуемой прямым и обратным проводом,
- индуктивности петли, образуемой прямым и обратным проводом, - проводимость утечки между проводами,
- проводимость утечки между проводами, - емкость между проводами.
- емкость между проводами.
 - напряжение между верхним и нижним проводами в точке х,
- напряжение между верхним и нижним проводами в точке х, - приращение напряжения на участке
- приращение напряжения на участке  ,
, - ток в точке х,
- ток в точке х, - приращение тока на участке
- приращение тока на участке 

 , т.е. ввести новую переменную
, т.е. ввести новую переменную 
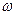 , тогда уравнения в комплексной форме
, тогда уравнения в комплексной форме
 ,
,
 - коэффициент распространения.
- коэффициент распространения.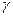 , получим:
, получим:
 .
.
 - волновое сопротивление линии.
- волновое сопротивление линии.
 и
и  в показательной форме, то получим мгновенные значения напряжения и тока:
в показательной форме, то получим мгновенные значения напряжения и тока: .
.
 и затухающую в направлении движения. Фазовой скоростью волны называется скорость перемещения фазы колебания, которая в течение времени
и затухающую в направлении движения. Фазовой скоростью волны называется скорость перемещения фазы колебания, которая в течение времени  Длиной волной
Длиной волной  называется расстояние между ближайшими двумя точками, взятое в направлении распространения волны, фазы колебания в которых различаются на
называется расстояние между ближайшими двумя точками, взятое в направлении распространения волны, фазы колебания в которых различаются на  :
:  . Волну, движущуюся от начала линии называют прямой, а от конца линии – обратной.
. Волну, движущуюся от начала линии называют прямой, а от конца линии – обратной.


